Знакопеременные ряды

Определение. Числовой ряд , элементы которого имеют чередующиеся знаки, называется знакочередующимся.

Знакочередующийся ряд можно записать так:

Теорема 10 (признак Лейбница сходимости знакочередующегося ряда). Если элементы знакочередующегося ряда 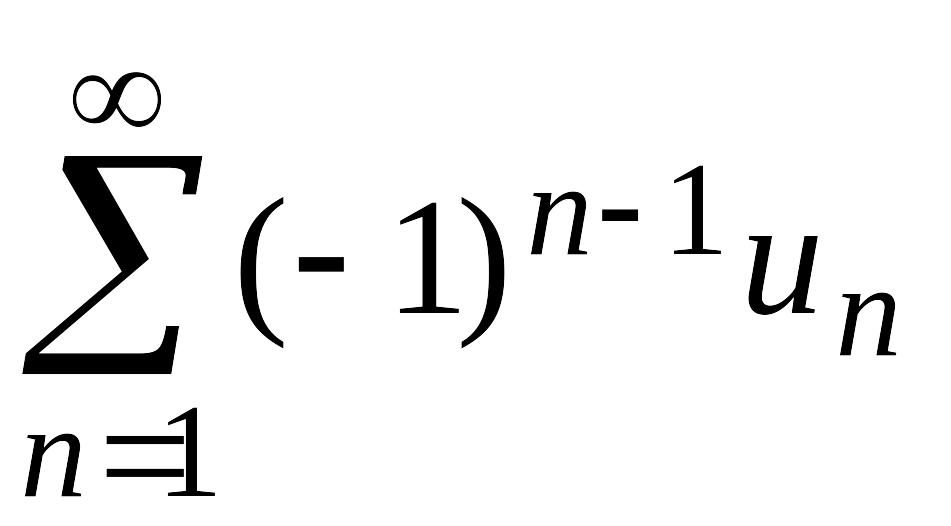удовлетворяют условиям:

1)

2) , то исходный ряд сходится, его сумма положительна и не превосходит первого элемента.

Замечание. Теорема справедлива, если условие выполняется, начиная с некоторого номера N.

Определение. Ряд называется знакопеременным, если среди его элементов имеются как положительные, так и отрицательные элементы.

Знакочередующийся ряд – частный случай знакопеременного ряда.

Теорема 11 (достаточный признак сходимости знакопеременного ряда). Если знакопеременный ряд таков, что ряд, составленный из абсолютных величин его элементов сходится, то и данный ряд также сходится.

Определение. Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его элементов:

Если же исходный знакопеременный ряд сходится, а ряд из абсолютных величин его элементов расходится, то данный знакопеременный ряд называется условно сходящимся.

Свойства абсолютно и условно сходящихся рядов

Теорема 12. Если числовой ряд сходится абсолютно, то он остается абсолютно сходящимся при любой перестановке его элементов. При этом сумма ряда не зависит от порядка его элементов.

Теорема 13. Если числовой ряд сходится условно, то какое бы мы ни взяли число А, можно так переставить элементы этого ряда, что его сумма окажется равной А. Более того, можно так переставить элементы условно сходящегося ряда, что ряд, полученный после перестановки, окажется расходящимся.

Пример 8. Исследовать на сходимость ряд .

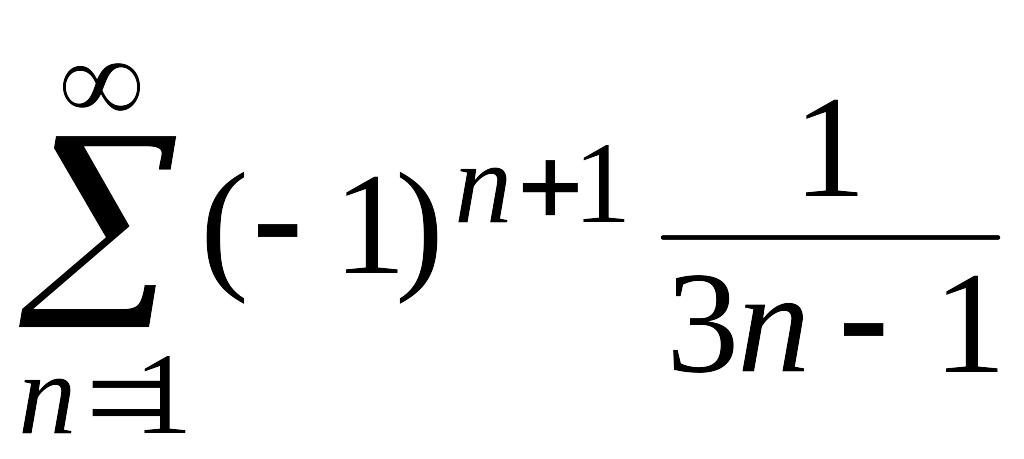Решение. Ряд знакочередующийся. Применяем признак Лейбница:

1)

2)

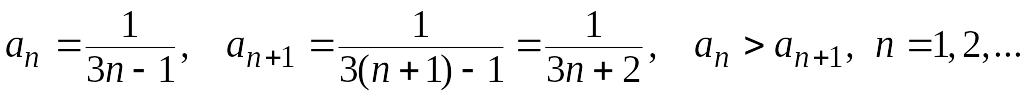
Из 1), 2) следует, что данный ряд сходится.

Исследуем ряд на абсолютную сходимость, составим ряд из абсолютных величин: 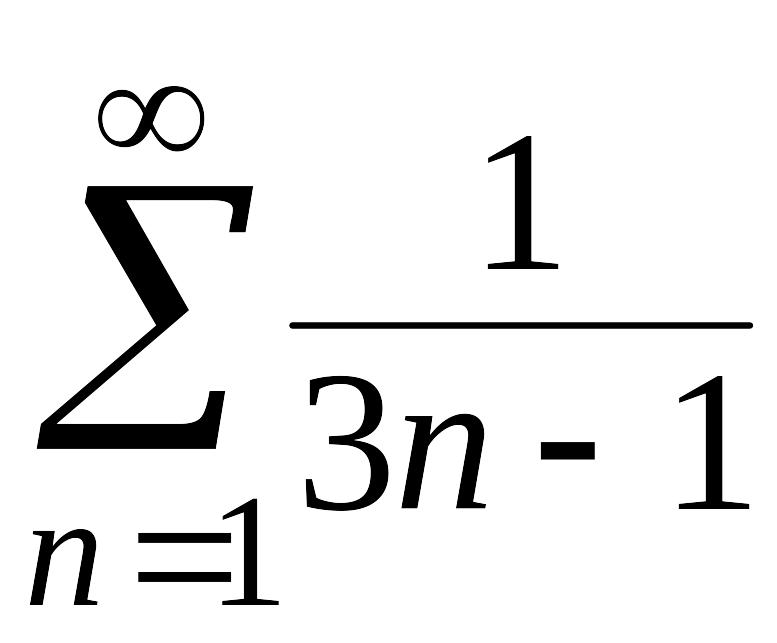. К полученному ряду применим предельный признак сравнения с рядом 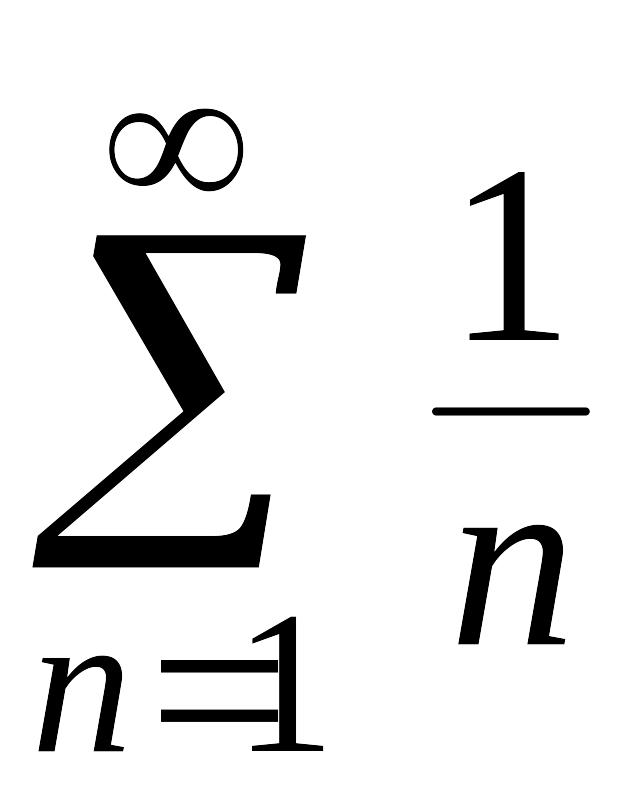. Члены выбранного и нового рядов – действительные положительные числа, при этом

.

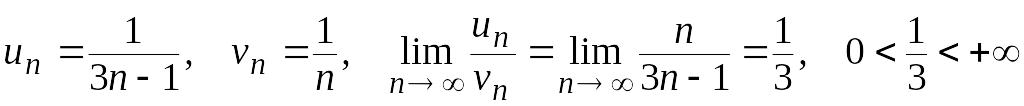Значит, эти ряды либо одновременно сходятся, либо одновременно расходятся. Т.к. ряд - расходящийся, то ряд также расходится.

Вывод: сходится условно.

Пример 9. Исследовать на сходимость ряд .

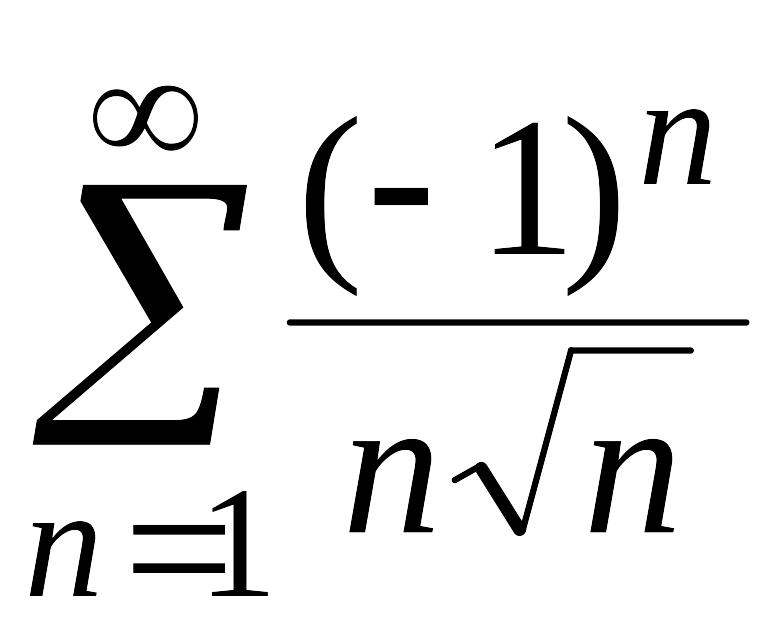Решение. Ряд знакочередующийся. Применяем признак Лейбница:

1)

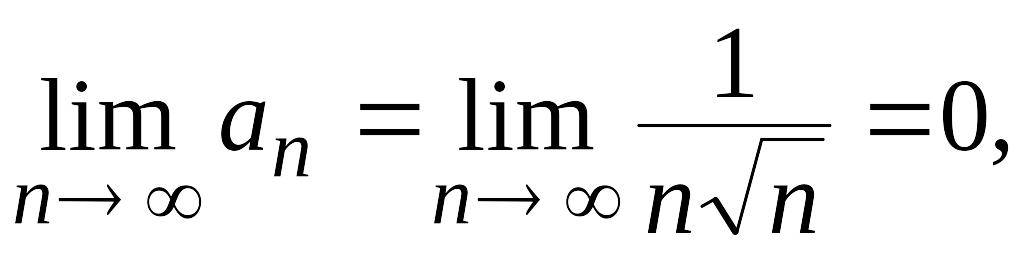
2)

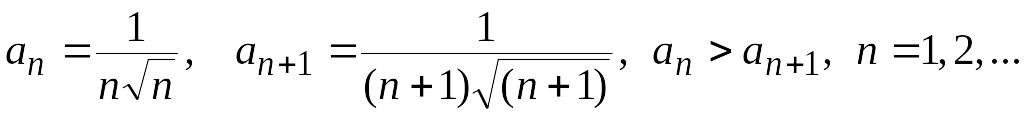
Условия признака выполняются, значит, ряд сходится. Исследуем этот ряд на абсолютную сходимость.

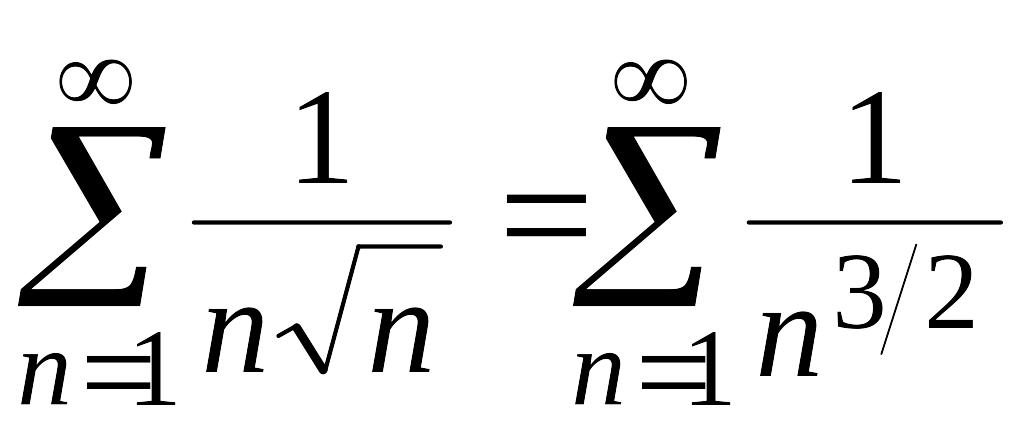. Получили ряд Дирихле 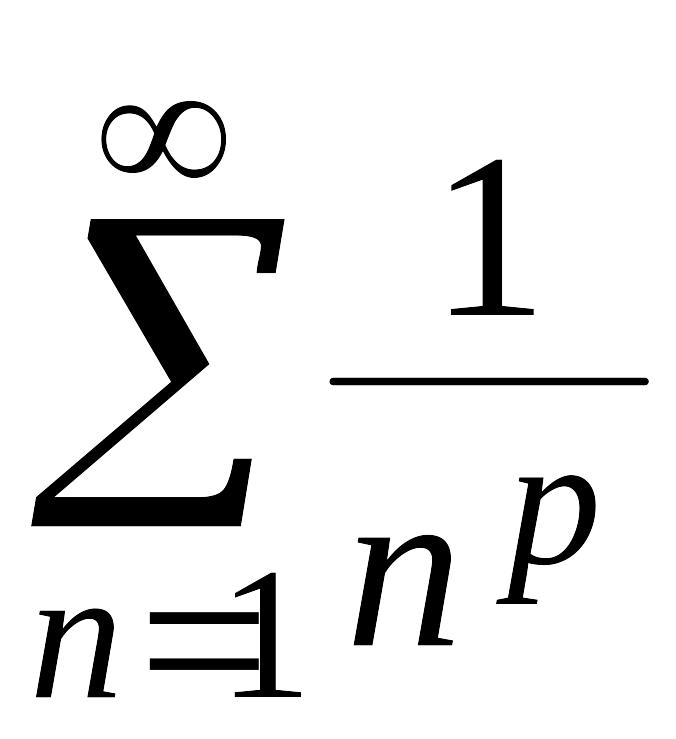(который при сходится, а при расходится). В нашем случае , поэтому ряд 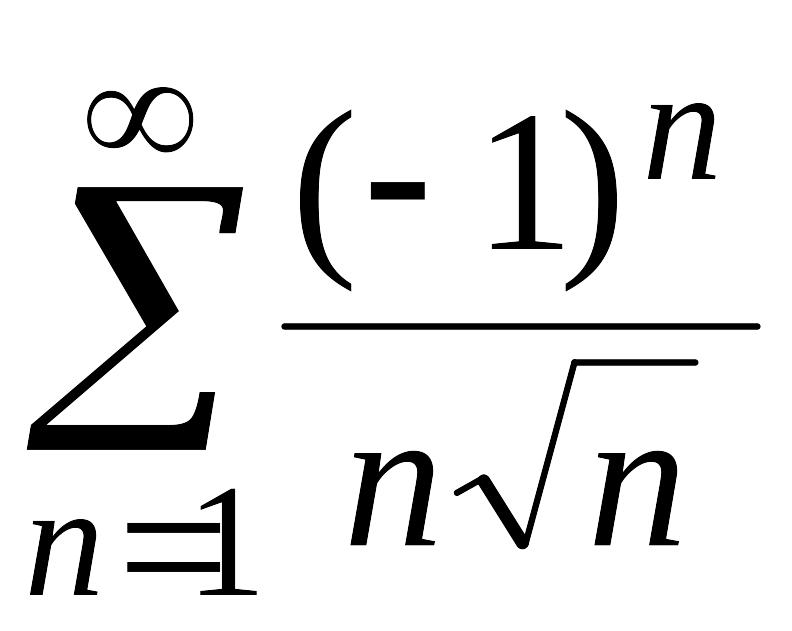сходится абсолютно.

Пример 10.

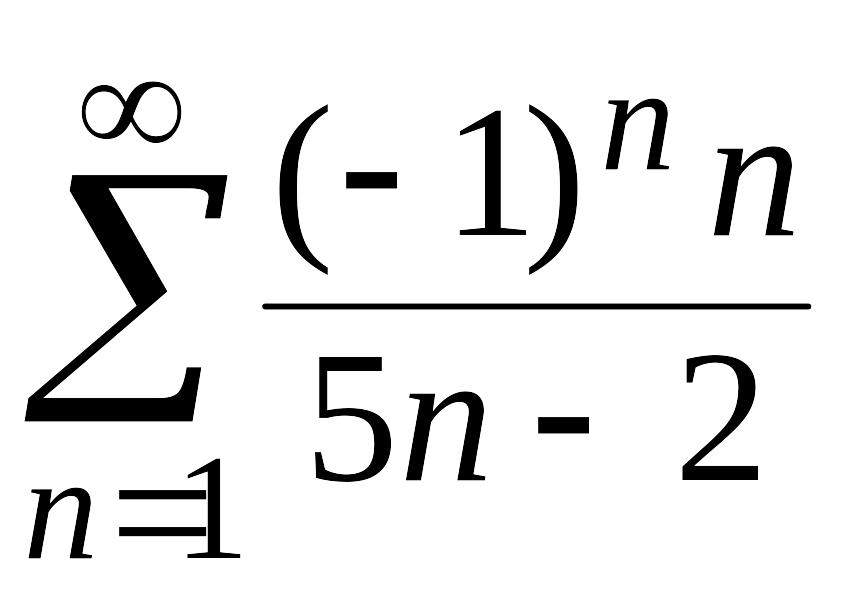
Решение. Ряд знакочередующийся. Применяем признака Лейбница:

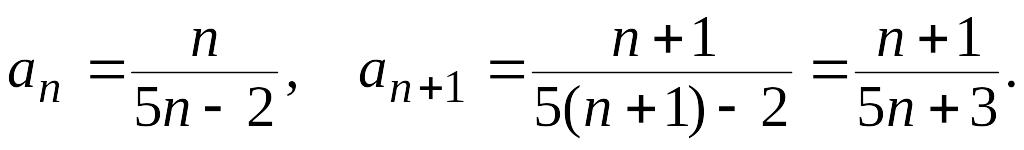
1) Нужно показать, что для любого п. Имеем

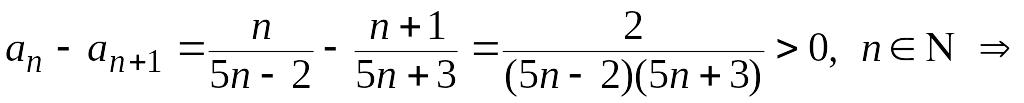
2) .

Вывод: ряд расходится.

Функциональные ряды

Ряд называют функциональным, если его элементы являются функциями от х, то есть .

Рассмотрим функциональный ряд 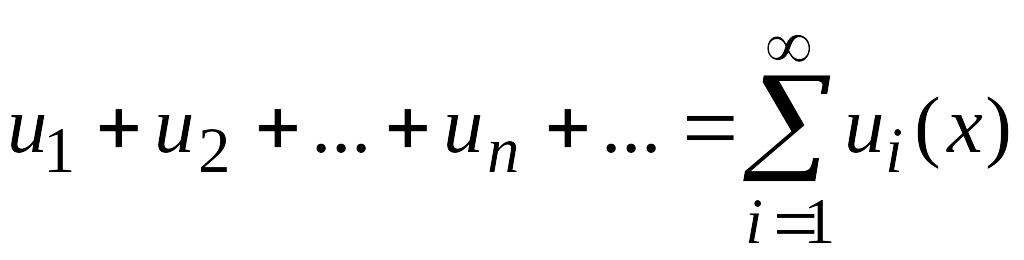. Придавая х определенные числовые значения, будем получать различные числовые ряды, которые могут оказаться как сходящимися, так и расходящимися.

Определение. Совокупность значений х, при которых функциональный ряд 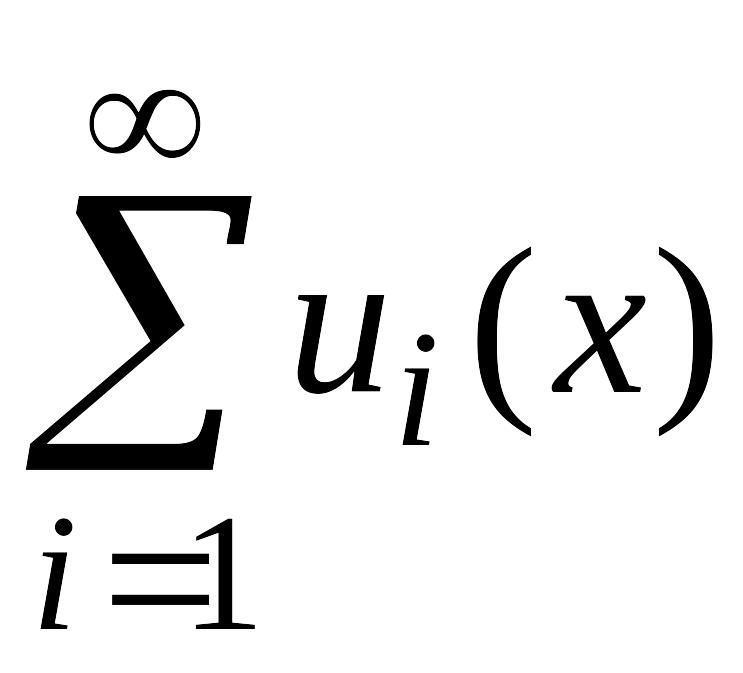сходится, называют областью сходимости этого ряда.

В области сходимости функционального ряда его сумма является некоторой функцией от х, поэтому принято обозначение .

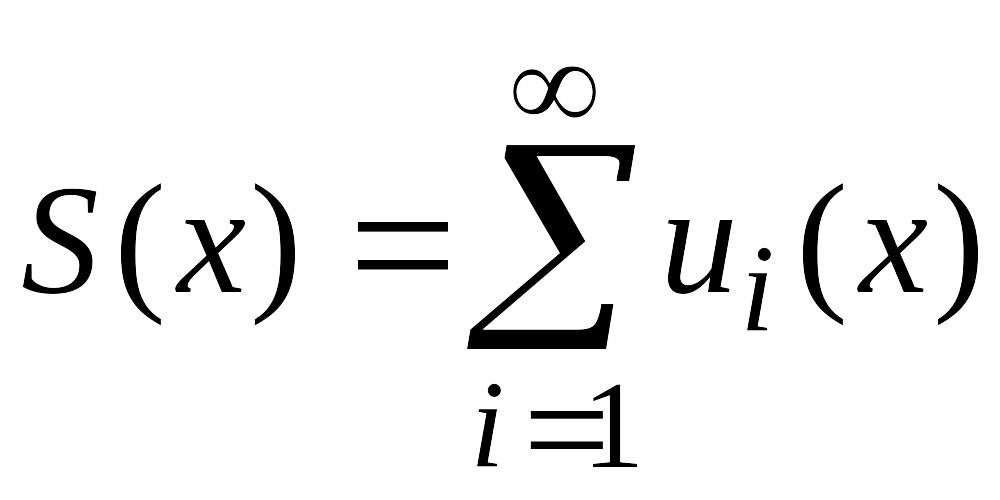Определение. Функциональный ряд называется мажорируемым в некоторой области изменения х, если существует такой сходящийся числовой ряд 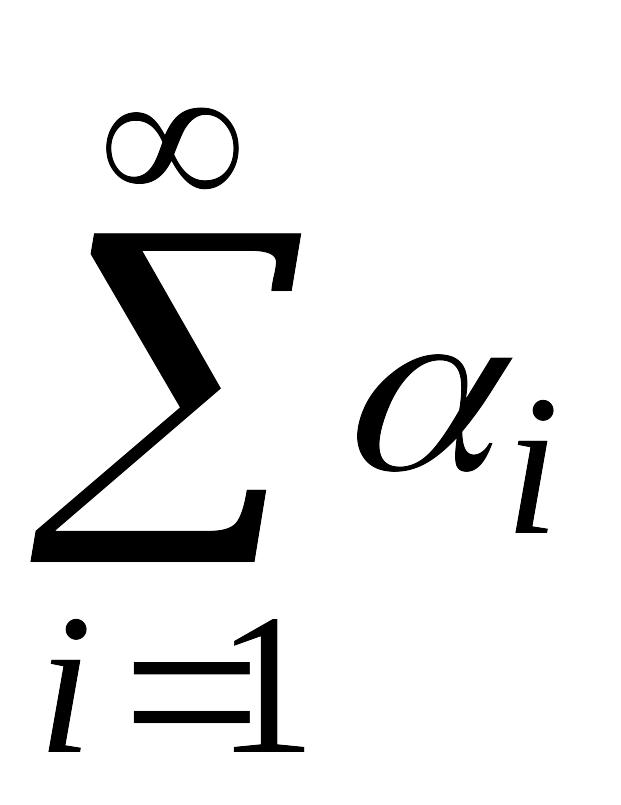с положительными элементами , что для всех значений х из данной области выполняется соотношение: для всех значений

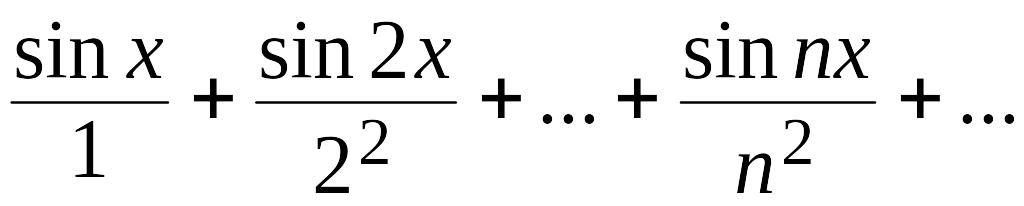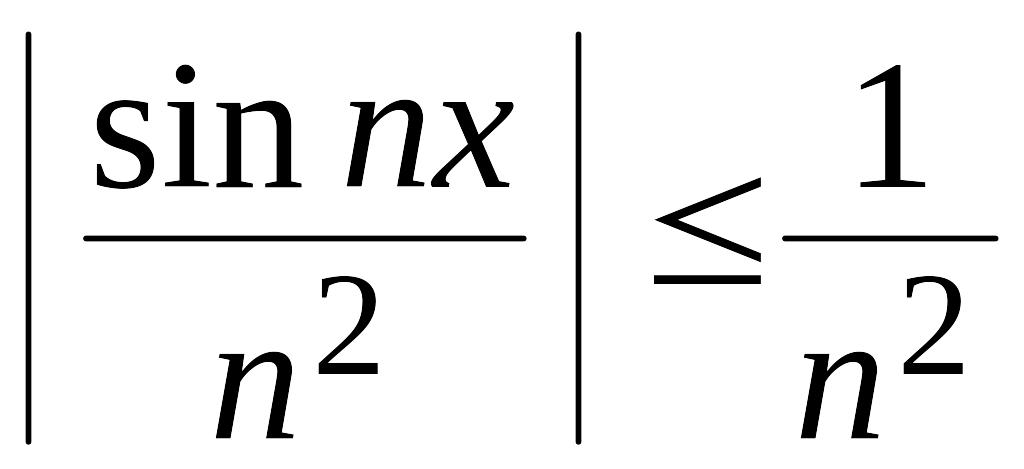Например, ряд мажорируем на всей оси Ох, так как для всех значений х: ; а ряд 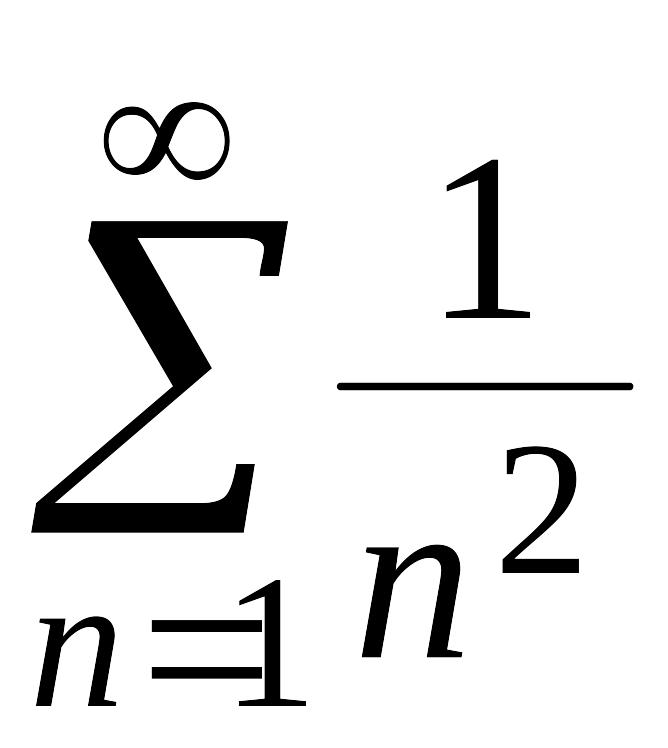является сходящимся.