Формула Крамера

Система линейных уравнений, в которой число уравнений равно числу неизвестных и определитель матрицы системы не равен 0, имеет единственное решение, определяемое по формулам Крамера:

где - определитель матрицы системы; - определитель, получаемый из определителя заменой -го столбца столбцом свободных членов.

Пример 1. Решить систему уравнений

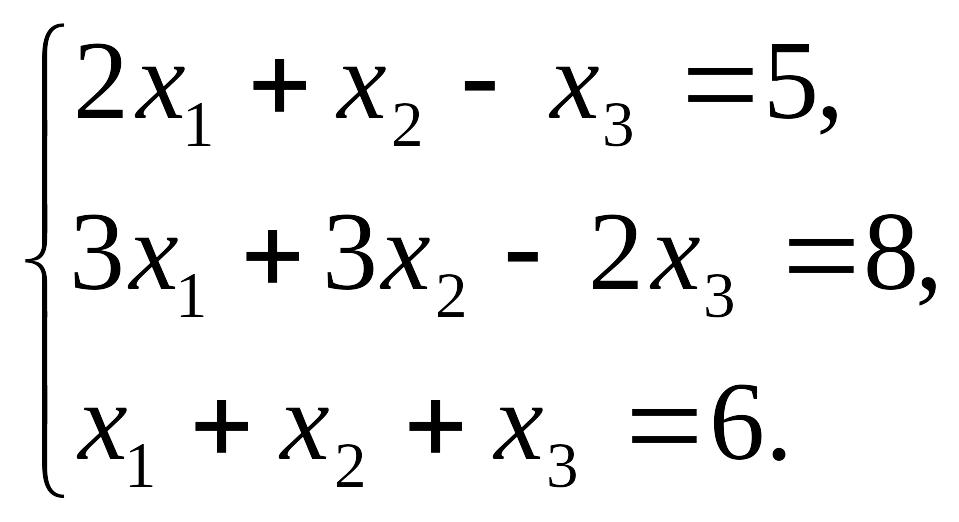
Решение. Вычислим определитель матрицы системных уравнений:

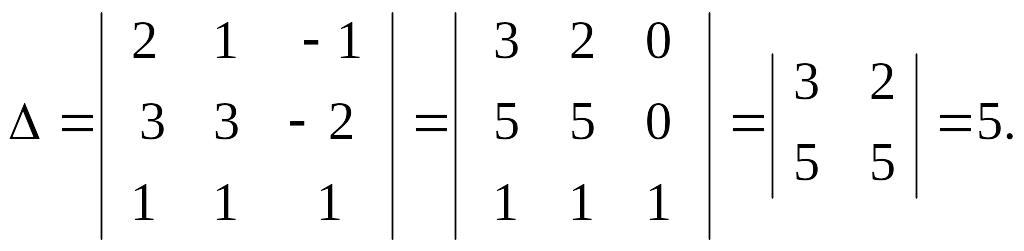
Следовательно, система имеет единственное решение, которое можно найти с помощью формул Крамера. Вычислим определители:

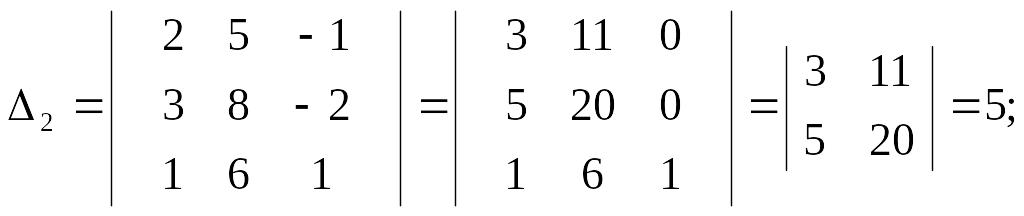
По формулам Крамера находим:

Метод Гаусса

Одним из наиболее универсальных и эффективных методов решений линейных алгебраических систем является метод Гаусса, состоящий в по­следовательном исключении неизвестных.

Пусть дана система уравнений:

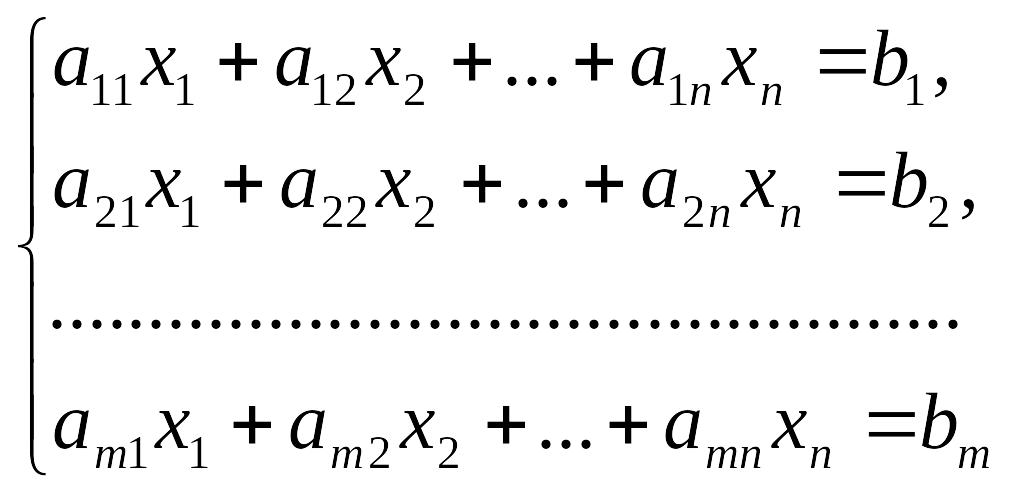
Процесс решения по методу Гаусса состоит из двух этапов. На первом этапе (прямой ход) система приводится к ступенчатому (в частности, треугольному) виду.

Приведенная ниже система имеет ступенчатый вид

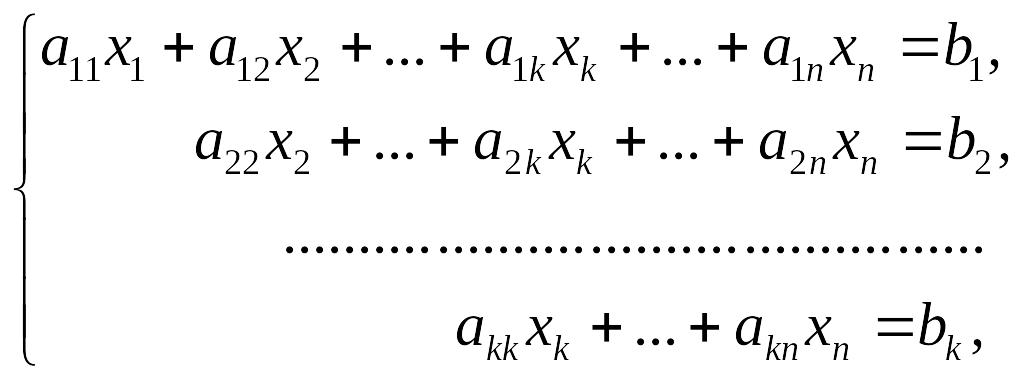
где . Коэффициенты а_ii называются главными элементами системы.

На втором этапе (обратный ход) идет последовательное определение неизвестных из этой ступенчатой системы. Опишем метод Гаусса подробнее.

Прямой ход.

Будем считать, что элемент (если а₁₁ = 0, то первым в системе запишем уравнение, в котором коэффициент при х₁ отличен от нуля).

Преобразуем систему, исключив неизвестное х₁ во всех уравне­ниях, кроме первого (используя элементарные преобразования системы). Для этого умножим обе части первого уравнения на и сложим почленно со вторым уравнением системы. Затем умножим обе части первого уравнения на и сложим с третьим уравнением системы. Продолжая этот процесс, получим эквивалентную систему:

Здесь — новые значения коэффициентов и правых частей, которые получаются после первого шага.

Аналогичным образом, считая главным элементом , исключим неизвестное x₂ из всех уравнений системы, кроме первого и второго, и так далее. Продолжаем этот процесс, пока это возможно.

Если в процессе приведения системы к ступенчатому виду по­явятся нулевые уравнения, т. е. равенства вида 0 = 0, их отбрасывают. Если же появится уравнение вида 0 = b_i, а то это свидетельствует о несовместности системы.

Второй этап (обратный ход) заключается в решении ступенчатой си­стемы. Ступенчатая система уравнений, вообще говоря, имеет бесчислен­ное множество решений. В последнем уравнении этой системы выражаем первое неизвестное x_к через остальные неизвестные (х_к+1,…,х_п). Затем подставляем значение x_к в предпоследнее уравнение системы и выражаем x_k-1 через (х_к+1,…,х_п); затем находим х_к-2,…,х₁ . Придавая свобод­ным неизвестным (х_к+1,…,х_п) произвольные значения, получим бесчи­сленное множество решений системы.

Замечание 1. Если ступенчатая система оказывается треугольной, т.е. , то исходная система имеет единственное решение. Из последнего уравнения находим , из предпоследнего уравнения , далее поднимаясь по системе вверх, найдем все остальные неизвестные ( )

Замечание 2. На практике удобнее работать не с исходной системой, а с расширенной матрицей, выполняя все элементарные преобразования над ее строками. Удобно, чтобы коэффициент был равен 1(для этого уравнения можно переставить местами, либо разделить обе части уравнения на ).

Пример 1. Решить систему уравнений

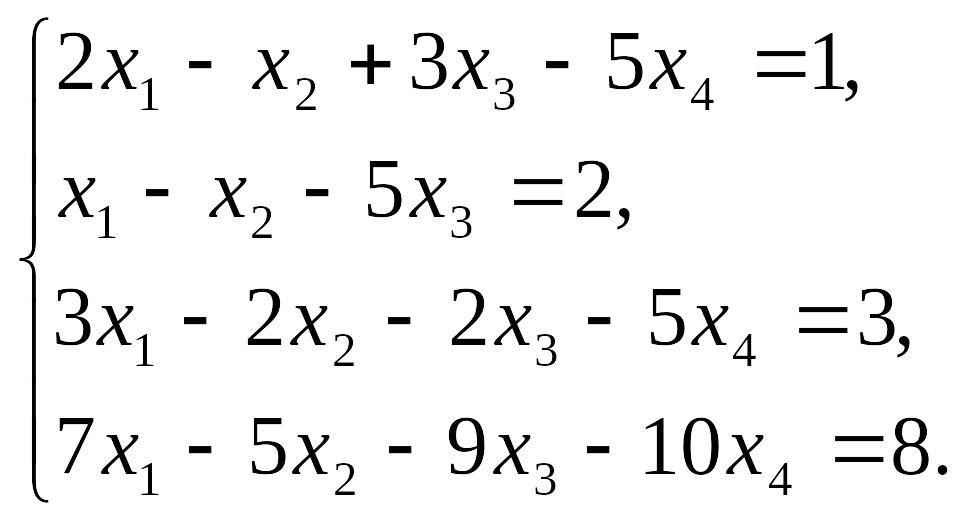
Решение. В результате элементарных преобразований над расширенной матрицей системы

Исходная система свелась к ступенчатой:

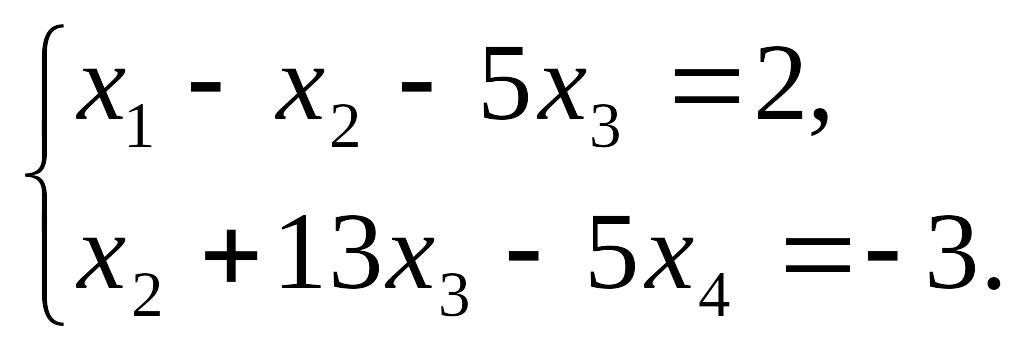
Поэтому общее решение системы: Если положить, например, , то найдем одно из частных решений этой системы

Пример 2. Решить систему методом Гаусса:

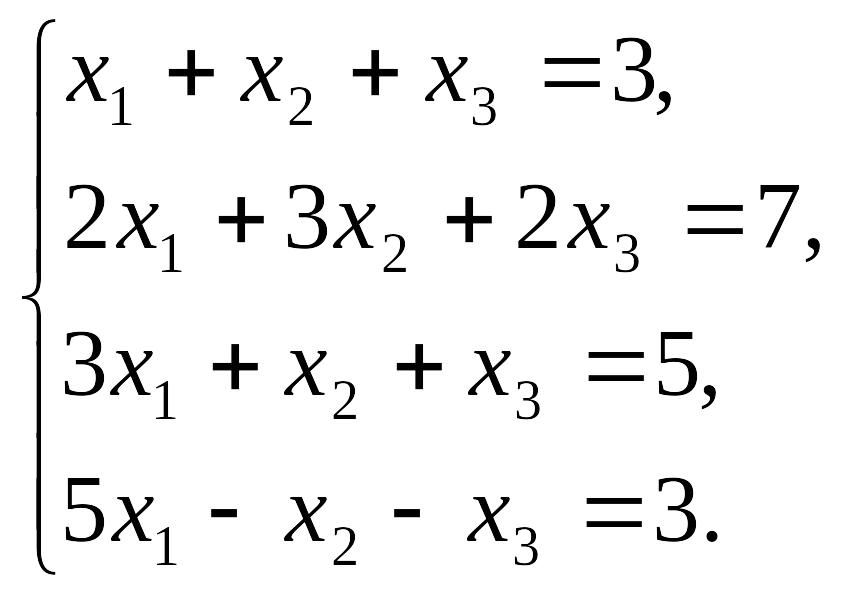
Решение. Произведём элементарные преобразования над строчками расширенной матрицы системы:

Полученная матрица соответствует системе

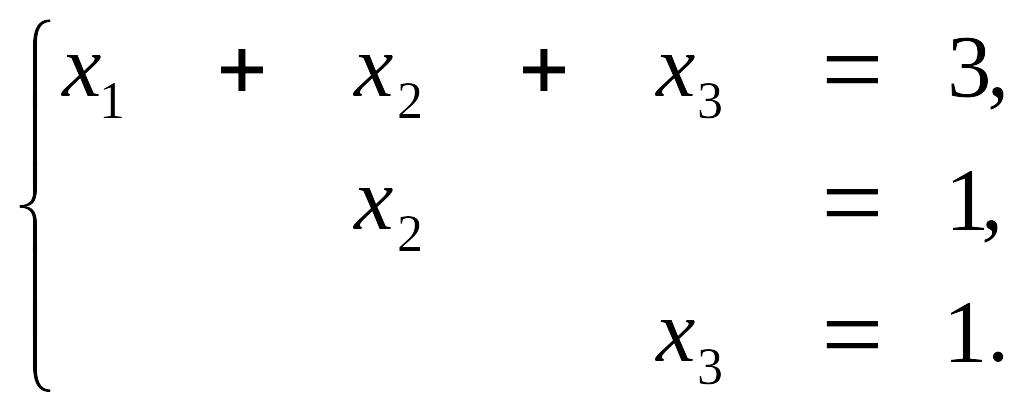
Осуществляя обратный ход, находим x₃=1, x₂=1, x₁=1.