5. Неопределённый интеграл
Определение.
Функция
называется первообразной
от функции
на отрезке
,
если во всех точках этого отрезка
выполняется равенство
.
Теорема.
Если
и
– две первообразные от функции
на отрезке
,
то разность между ними равна постоянному
числу.
Из
данной теоремы следует, что если
является первообразной для функции
,
то
,
где
,
также является первообразнй для функции
.
Определение.
Если
является первообразной для функции
,
то выражение
называется неопределенным
интегралом
от функции
и обозначается символом
,
т.е.
,
где
называют подынтегральной функцией,
– подынтегральным выражением,
–
знак интеграла.
Теорема
(теорема существования).
Если функция непрерывна на отрезке
,
то она интегрируема на этом отрезке.
Свойства неопределенного интеграла
Правила вычисления интегралов
Если
,
то
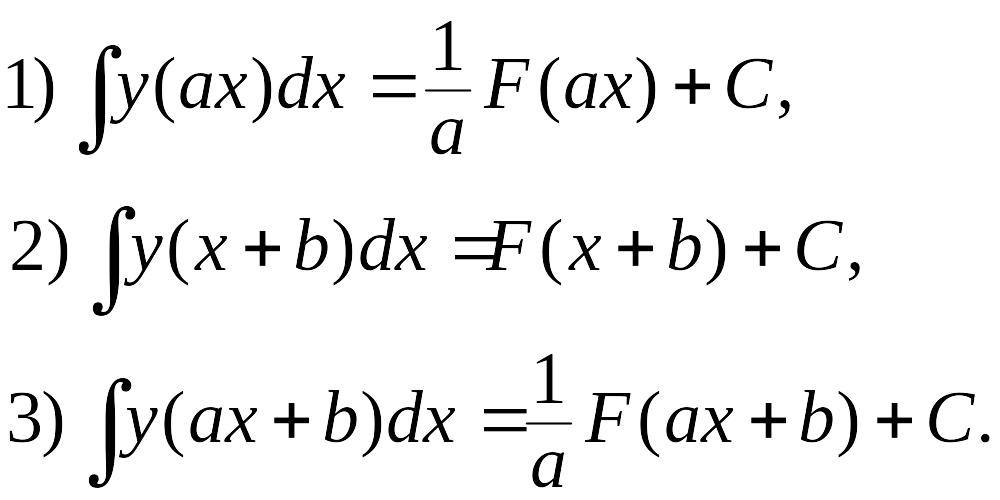
Таблица основных интегралов
1)
|
8)
|
2)
|
9)
|
3)
|
10)
|
4)
|
11)
|
5)
|
12)
|
6)
|
13)
|
7)
|
14)
|
Методы интегрирования Метод непосредственного интегрирования
Этот метод основан на использовании правил интегрирования, свойств неопределенного интеграла, таблицы основных интегралов и тождественных преобразований подынтегральной функции.
Пример
1. Вычислить
Решение. Выделив полный квадрат в знаменателе подынтегральной функции, получим табличный интеграл:
Пример
2. Вычислить
Решение. Используя свойства интегралов, таблицу основных интегралов и правила интегрирования, получаем:
Метод замены переменной и внесение под знак дифференциала
Указанные операции применяются для того, чтобы упростить подынтегральное выражение.
Пример
3. Вычислить
Решение.
Пример
4. Вычислить
Решение.
Метод интегрирования по частям
Формула
интегрирования по частям:
При использовании данного метода, наиболее часто встречаются следующие три основных случая:
В подынтегральном выражении – две функции, от одной существует табличный интеграл, а от другой – нет. В этом случае функцию, от которой не существует табличного интеграла обозначают через u.
В подынтегральном выражении – две функции, от каждой из которых существуют табличные интегралы, но одна из них представляет собой многочлен. В этом случае через u обозначают многочлен.
В подынтегральном выражении – две функции, от каждой из которых существуют табличные интегралы. При этом одна функция тригонометрическая, например,
,
а вторая не является многочленом. В
этом случае для единообразия, через u
обозначают тригонометрическую функцию.
Пример
5. Вычислить
Решение.
В подынтегральном выражении представлены
две функции
От функции
существует табличный интеграл, от
– не существует. Этот пример относится
к первому случаю формулы интегрирования
по частям. За u
принимаем функцию, от которой нет
табличного интеграла.
Пример
6. Вычислить
Решение.
В подынтегральном выражении можно
выделить две функции
От обеих функций существует табличный
интеграл, но
является многочленом. В данной ситуации
имеем второй случай формулы интегрирования
по частям.
Пример
7. Вычислить
Решение.
Структура подынтегрального выражения
приводит к третьему случаю формулы
интегрирования по частям:
В результате применения интегрирования по частям, получаем уравнение относительно исходного интеграла:
.
Откуда следует, что
или
и,
окончательно:
