Линейные дифференциальные уравнения с постоянными коэффициентами
Определение.
Дифференциальное уравнение n-ого
порядка называется линейным,
если оно первой степени относительно
исходной функции y(x)
и ее производных
,
где
.
Если
являются
постоянными числами, то уравнение
называется линейным дифференциальным
уравнением n-ого
порядка с постоянными коэффициентами.
Если
,
то указанное выше уравнение называется
линейным однородным,
а в случае
– неоднородным
линейным дифференциальным уравнением
n-ого
порядка.
Линейные однородные дифференциальные уравнения
Рассмотрим линейное однородное дифференциальное уравнение n-ого порядка с постоянными коэффициентами:
.
Теорема.
Если
являются
линейно независимыми решениями линейного
однородного дифференциального уравнения
n-ого
порядка с постоянными коэффициентами,
то общее решение этого уравнения имеет
вид
,
где
–
произвольные постоянные.
Для нахождения линейно независимых решений линейного однородного дифференциального уравнения n-ого порядка необходимо выполнить следующие действия:
1. Составляем характеристическое уравнение:
2.
Находим корни этого характеристического
уравнения:
;
3. По характеру корней выписываем частные линейно независимые решения, руководствуясь тем, что:
а)
каждому действительному однократному
корню соответствует частное решение
;
б) каждой
паре комплексных сопряженных однократных
корней
соответствуют
два частных действительных решения:
и
;
в)
каждому действительному корню k
кратности r
соответствуют r
линейно независимых частных решений:
;
г) каждой
паре комплексных сопряженных корней
кратности
соответствуют 2
действительных частных решений:
,
.
Этих частных решений будет ровно столько, какова степень характеристического уравнения. Самостоятельно основываясь на определении линейной независимости для функций, предлагается убедиться, что полученные частные решения будут линейно независимыми.
4.
Получив n
линейно независимых частных решений
,
строим
общее решение исходного линейного
однородного дифференциального уравнения
с постоянными коэффициентами:
.
Пример
6.
.
Решение. Составляем характеристическое уравнение:
.
Записываем линейно независимые частные решения
.
Получаем
общее решение :
.
Линейные неоднородные дифференциальные уравнения
Рассмотрим
неоднородное линейное дифференциальное
уравнение с постоянными коэффициентами
.
Теорема.
Общее решение неоднородного уравнения
равно сумме общего решения соответствующего
однородного уравнения
и
частного решения неоднородного уравнения
:
.
Для отыскания частного решения неоднородного дифференциального уравнения существует два способа. Первый способ (он является универсальным) называют методом вариации произвольных постоянных, а второй – подбором частного решения по виду правой части неоднородного уравнения.
Метод
вариации произвольных постоянных
заключается в том, что величины
в общем решении однородного уравнения
считают не постоянными, а функциями от
х.
При этом они должны удовлетворять
системе уравнений:
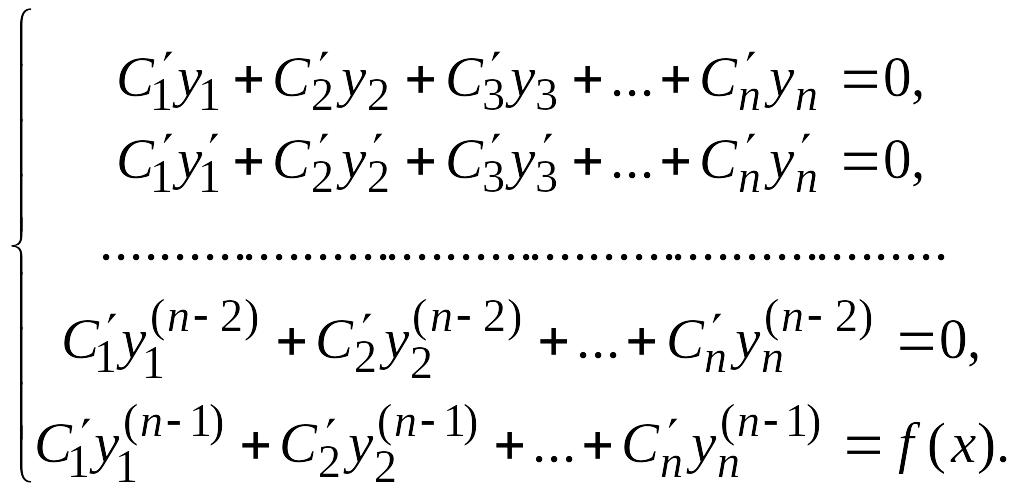
Эта система имеет единственное решение.
Окончательно,
выражение
будет является общим решением исходного
неоднородного дифференциального
уравнения, где
получаем при решении системы
дифференциальных уравнений, указанной
выше.
Пример
7.
.
Решение. Найдем общее решение однородного уравнения :
Составляем
систему уравнений для нахождения
и
:
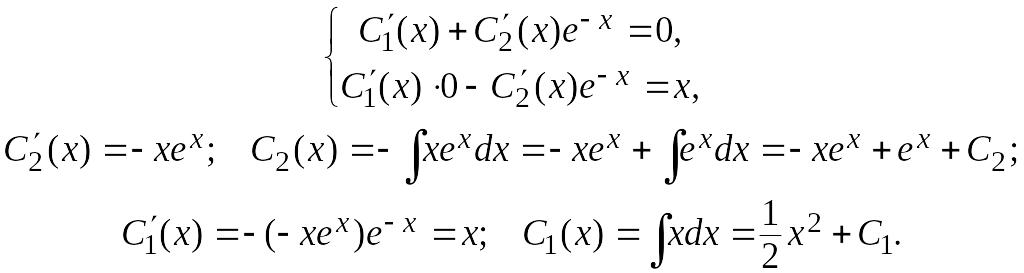
Окончательно получаем общее решение неоднородного уравнения:
Подбор частного решения по виду правой части неоднородного уравнения заключается в следующем. Допустим, что правая часть неоднородного уравнения имеет структуру:
,
где
и
– многочлены степени n
и m
соответственно.
Частное решение неоднородного уравнения строим в виде:
.
Имея
конкретную функцию
правой части неоднородного дифференциального
уравнения, определяем значения величин
n,
m,
α, β.
Параметры
структуры частного решения неоднородного
дифференциального уравнения учн:
μ, е, α, β,
определяются
следующим образом: значения α
и β в
структуре частного решения учн
совпадают с α
и β
в структуре правой части
исходного
неоднородного дифференциального
уравнения. Если значение
совпадает со значением корня
характеристического уравнения
соответствующего однородного
дифференциального уравнения, то μ
равно значению кратности этого корня,
в противном случае
Величина
,
а сами многочлены
и
записываются в общем виде с неизвестными
коэффициентами, которые определяются
из условия, что частное решение учн
должно удовлетворять исходному
неоднородному линейному дифференциальному
уравнению.
Пример
8.
.
Решение. Характеристическое уравнение соответствующего однородного уравнения имеет вид:
В соответствии с корнями характеристического уравнения, общее решение однородного уравнения будет иметь вид:
.
Исходя из вида правой части данного уравнения, получаем:
Значение
совпадает с корнем характеристического
уравнения. Кратность этого корня равна
1. Поэтому
,
Тогда многочлены
и
представляют собой многочлены нулевой
степени с неизвестными коэффициентами,
которые можно записать так:
Таким
образом, структура частного решения
неоднородного уравнения принимает вид:
.
Находим все производные от учн, входящие в исходное уравнение:
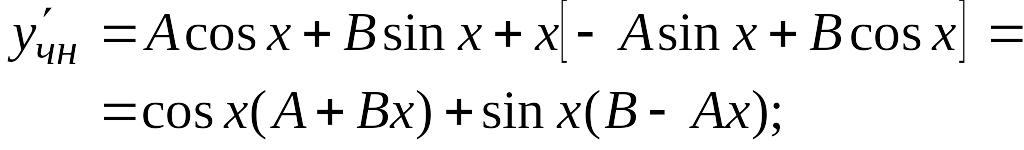
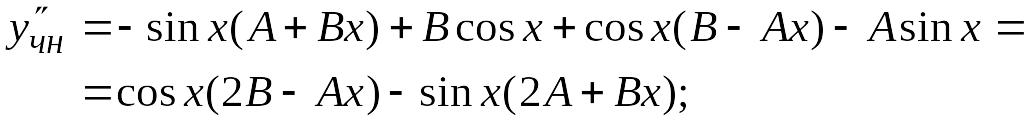
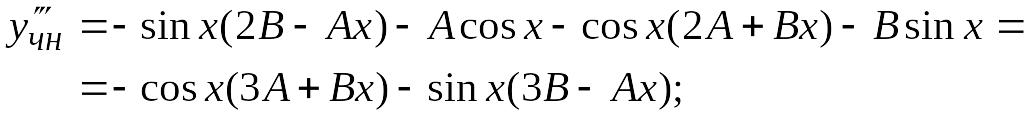
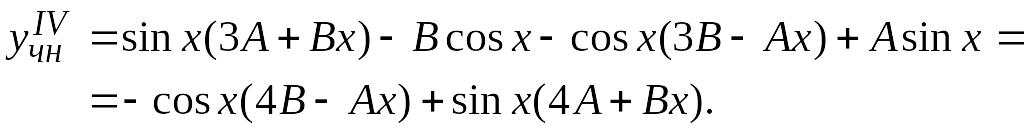
Подставляем
выражение
и
в исходное уравнение:
,
.
Из последнего, требуя выполнения тождества, находим:
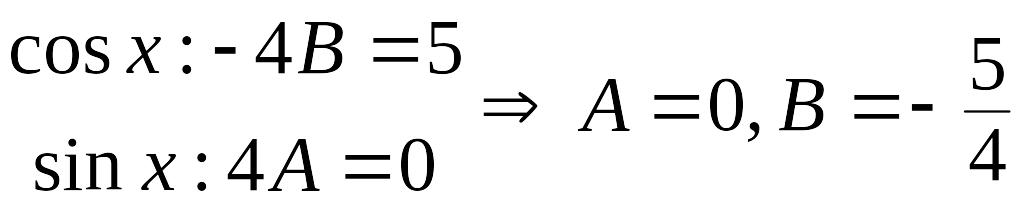
Частное
решение
принимает вид:
,
а общим решением
неоднородного
уравнения будет
