22. Дифференцируемость случайных процессов.

Опр. Случайный процесс ξ(t) называется дифференцируемым в среднем квадратичном в точке t₀, если существует передел

Случайная функция ξ’(t₀) называется среднеквадратичной производной процесса в точке t₀.

Т.1. (критерий дифференцируемости в среднем квадратичном). Для того чтобы процесс ξ(t) был дифференцируемым в среднем квадратичном в точке t₀, необходимо и достаточно, чтобы существовала частная смешанная производная второго порядка корреляционной функции в точке t₀=t₁=t₂.

Док-во. Обозначим

Тогда по критерию сходимости в среднем квадратичном для существования производной ξ’(t₀) необходимо и достаточно существование предела

Имеем:

Последняя частная производная, по условию теоремы, существует, а значит, существует предел (1).

Т.2. если для всех t T существует вторая смешанная производная от корреляционной функции при совпадающих аргументах , то существуют первые и вторая смешанные производные при несовпадающих аргументах

Док-во. Действительно, исходя из предыдущей теоремы, существование означает существование ξ’(t₁). Обозначив

Также существует предел

23. Интегрирование случайных процессов.

Пусть случайный процесс ξ(t) и неслучайная функция заданы на интервале [a,b]. Разобьем этот интервал точками a=t₁<t₂<…<t_n=b.

Опр. Случайный процесс ξ(t) интегрируем в среднем квадратичном на отрезке [a,b], если существует конечный предел в среднем квадратичном интегральных сумм:

Т.1. (критерий интегрируемости случайного процесса в среднем квадратичном). Для того чтобы процесс ξ(t) был интегрируем в среднем квадратичном, необходимо и достаточно, чтобы существовал двойной интеграл от его корреляционной функции

Док-во. по критерию сходимости, для существования интеграла (1) необходимо и достаточно существование предела

Т.к.

то как раз в качестве А можно взять двойной интеграл (2).

Под несобственными интегралами в среднем квадратичном будем понимать соответственно пределы

24. Стохастические обыкновенные дифференциальные уравнения.

Под стохастическим обыкновенным дифференциальным уравнением обычно понимается дифференциальное уравнение относительно среднеквадратичной производной случай­ного процесса. Рассмотрим линейное дифференциальное уравнение первого порядка

ξ'(t) +a(t)ξ(t)=η(t) (1)

удовлетворяющее начальному условию ξ(0) = х₀, где а(t) действи­тельная функция, η(t), t≥ 0, - известный случайный процесс, х₀ -заданное число. Рассмотрим взаимную функцию корреляции процессов ξ(t) и η(t) R_ξη(t₁,t₂). Определяя среднее значение от обеих сторон уравнения (1), получим

Найдем теперь дифференциальное уравнение для корреляционной функции R_ξη(t₁,t₂). Сначала умножим обе стороны уравнения (1) при t= t₁, на η(t₂) и определим средние значения для обеих сто­рон. Тогда будем иметь

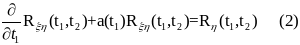
Можно найти решение этого уравнения при начальном условии R_ξη(0,t₂)=x₀m_η(t₂). Далее, умножив обе стороны уравнения (1) при t= t₂, на ξ(t₁) и определив средние значения, получим

для которого можно также найти решение при начальном условии R_ξη\(t₁,0)=x₀m_ξ(t₁).

Рассмотренный метод можно также применить в случае, ког­да в качестве х₀ берется некоторая СВ.