
- •1. Классическое и геометрическое определение вероятности, элементы комбинаторики
- •2. Аксематическое определение вероятности. Свойства вероятности.
- •3. Формула полной вероятности. Формула Байеса.
- •4. Схема независимых испытаний Бернулли. Предельная теорема Пуассона.
- •5. Классификация случайных величин.
- •2) Непрерывные случайные величины.
- •6. Математическое ожидание и его свойства.
- •7. Дисперсия и ее свойства.
- •Свойства дисперсии:
- •8. Характеристические функции и их свойства.
- •Свойства характеристической функции :
- •Способы описания св:
- •9.Теорема об обращении характеристической функции.
- •1 1. Виды сходимости случайных последовательностей.
- •13.Критерий сходимости в среднем квадратичном.
- •15. Усиленный закон больших чисел.
- •16. Центральная предельная теорема.
- •10.Производящие функции и их свойства.
- •17. Определение случайного процесса.
- •19. Статистические средние характеристики случайных процессов.
- •20. Сходимость в среднем квадратичном для случайных процессов.
- •21. Непрерывность случайных процессов.
- •22. Дифференцируемость случайных процессов.
- •23. Интегрирование случайных процессов.
- •24. Стохастические обыкновенные дифференциальные уравнения.
- •25. Процессы с независимыми приращениями.
- •26. Гауссовский случайный процесс.
- •27. Винеровский случайный процесс.
- •28. Марковские случайные процессы и цепи маркова определения.
- •29. Однородные цепи Маркова.
- •32. Уравнения Чепмена-Колмогорова.
- •33. Нахождение вероятностей переходов с помощью производящих функций.
- •34. Классификация состояний цепи Маркова по арифметическим свойствам вероятностей перехода
- •35. Свойство периода состояния.
- •36. Классификация состояний по асимптотическим свойствам переходных вероятностей
- •37. Критерий возвратности состояний.
- •38.Эргодические цепи Маркова
- •40. О средних временах переходов между состояниями
- •41. Стационарные цепи Маркова
- •42. Оптимальные стратегии в марковских цепях
- •43. Система диф.Ур-ий Колмогорова для однородной цепи Маркова с конеч.Числом состояний.
- •44. Процесс гибели и размножения
- •49. Обобщенное уравнение Маркова
- •50.Диффузионные процессы
- •51. Обратное уравнение Колмогорова
- •45. Марковские системы массового обслуживания.
- •Рассмотрим систему с простейшим потоком и экспоненциальным обслуживанием
- •46. Система обслуживания м / м / 1
- •47.Система м / м / n / 0
- •48. Система обслуживания м / м / n
- •52.Прямое уравнение Колмогорова для диффузных процессов
- •53. Стохастический интеграл Ито
- •54. Стохастический интеграл в форме Стратоновича
- •55. Стохастические дифференциальные уравнения
- •39. Закон больших чисел для цепей Маркова с конечным числом состояний.
- •57. Стационарность гауссовского случ.Процесса.
- •58. Теорема Бохнера., спектральная плотность случ.Процесса.
- •60. Мартингалы.
- •18. Пуассоновский случ.Процесс
- •Классическое и геометрическое определение вероятности, элементы комбинаторики
1. Классическое и геометрическое определение вероятности, элементы комбинаторики
классическое определение вероятности.
Для
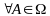 поставим в соответствие действительное
неотрицательное число р(А),
которое будем называть вероятностью
события А.
поставим в соответствие действительное
неотрицательное число р(А),
которое будем называть вероятностью
события А.
Определим
классическое вероятностное пространство.
Пусть
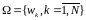 - конечное множество. Пусть
- конечное множество. Пусть
 ,
а
,
а
 .
Возьмём некоторое случайное событие
А,
которое получено путём объединения
.
Возьмём некоторое случайное событие
А,
которое получено путём объединения
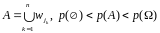 .
Если все элементарные события
.
Если все элементарные события
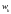 равновозможны, то естественно предположить,
что вероятность события А
пропорциональна числу элементарных
событий, которые оно объединяет, т.е.
равновозможны, то естественно предположить,
что вероятность события А
пропорциональна числу элементарных
событий, которые оно объединяет, т.е.
 .
Коэффициент пропорциональности р
можно найти из условия, что
.
Коэффициент пропорциональности р
можно найти из условия, что
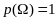
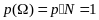
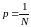
 (*). Т.е.
вероятность события А
равна отношению числа благоприятствующих
элементарных события событию А
к общему числу всех элементарных событий.
(*). Т.е.
вероятность события А
равна отношению числа благоприятствующих
элементарных события событию А
к общему числу всех элементарных событий.
Условие
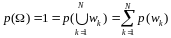 называется условием нормировки.
называется условием нормировки.
Говорят,
что определена вероятностная модель,
если определено множество
 элементарных
событий и на этих элементарных событиях
определена функция
элементарных
событий и на этих элементарных событиях
определена функция
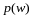 .
.
Для
рассматриваемого выше случая вероятностная
модель выглядит следующим образом:
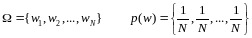 .
Т.е. для каждого элементарного события
вероятность равна
.
Т.е. для каждого элементарного события
вероятность равна
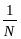 .
.
Данная
вероятностная модель называется
классической, а пара элементов
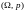 наз. классическим вероятностным
пространством.
наз. классическим вероятностным
пространством.
Классическая вероятностная модель определяет классическое вероятностное пространство. Для него:
1) множество элементарных событий конечно;
2) вероятности элементарных событий одинаковы.
В классической модели определение вероятности определяется следующим образом: определяется число элементарных событий, определяющих пространство , затем находится число элементарных событий, составляющих интересующее событие А, и находится отношение второго к первому – это и есть вероятность события А.
Элементы комбинаторики.
Для
подсчёта чисел n
и N
из формулы (*) применяются элементы
комбинаторики. Основной принцип
комбинаторики заключается в следующем:
если некий выбор А
можно осуществить n
способами, а выбор В
– m
способами, то выбор А
и В
можно осуществить
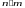 способами, а выбор А
или В
–
способами, а выбор А
или В
–
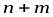 способами.
способами.
При решении задач в теории вероятности часто используются понятия размещение, сочетание, перестановка.
Определение.
Если дано некоторое множество
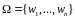 ,
то размещением n
элементов по k
называется любое упорядоченное
подмножество из k
элементов множества
.
Соответственно, сочетанием из n
элементов по k
называется любое неупорядоченное
подмножество из k
элементов множества
.
При
,
то размещением n
элементов по k
называется любое упорядоченное
подмножество из k
элементов множества
.
Соответственно, сочетанием из n
элементов по k
называется любое неупорядоченное
подмножество из k
элементов множества
.
При
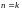 размещение называется перестановкой
из k
элементов.
размещение называется перестановкой
из k
элементов.
Два сочетания отличаются друг от друга хотя бы одним элементом. Размещения отличаются друг от друга либо одним элементом, либо порядком их следования.
Число
сочетаний находится по формуле
 .
.
Число
размещений находится по формуле
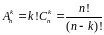 .
.
Геометрическое определение вероятности.
Геометрическое
определение вероятности является
расширением понятия классической
вероятности на случай несчётного
множества элементарных событий. В
случае, когда
является несчётным множеством, вероятность
определяется не на элементарных событиях,
а на их множествах. Пусть равновозможные
элементарные события w
являются точками ограниченного множества
n-мерного
Евклидова пространства
,
имеющего меру Лебега
 .
.
Рассмотрим
систему измеримых
по Лебегу подмножеств множества
.
Для любого случайного события
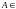
вероятность определяется по формуле
вероятность определяется по формуле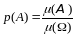 .
.
Под
мерой в частном случае понимается: длина
отрезка (если
 ),
площадь (если
),
площадь (если
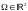 ),
объём (если
),
объём (если
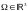 ).
).
Свойства меры Лебега: мера Лебега – это действительная, неотрицательная, счётно-аддитивная функция множеств, для которой:
1)
 3) если
3) если

2)
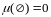 4)
4)
 ,
то
,
то
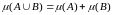
Недостатки геометрического определения вероятности:
мера пространства должна быть ограниченной;
все элементарные события
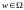 должны быть равновероятны.
должны быть равновероятны.
Пример.
Автобус №4 идет в данном направлении с интервалом в 10 минут. Студент приходит на остановку в случайный момент времени. Найти вероятность того, что студент будет ждать не более 1 минуты.
состоит
из точек интервалов длительностью 10
минут. Определим
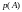 .
Событие А
= {студент ожидает автобус не более 1
минуты}.
будет состоять из точек интервала,
отстоящего от конца десятиминутного
интервала не более, чем на 1 минуту.
.
Событие А
= {студент ожидает автобус не более 1
минуты}.
будет состоять из точек интервала,
отстоящего от конца десятиминутного
интервала не более, чем на 1 минуту.
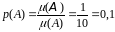 .
.
