40. О средних временах переходов между состояниями

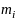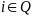Обозначим через Е_к мн-во состояний к -го эргодического класса, Q - множество несущественных состояний, -сред­нее время перехода из i-го несущественного состояния, , в -й эргодический класс. Найдем это время. Цепь Маркова за один шаг может перейти из i -го несуществен­ного состояния в некоторое состояние 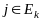с вер-тью ,

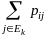тогда время перехода равно 1. Если же цепь за первый шаг перейдет в другое состояние вероятностью , то среднее время пере­хода в эргодический класс будет равно 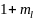, и окончательно имеем 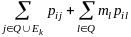(10.20)

Решая эту систему ур-ний относительно , полу­чим нужные нам средние времена. Если нас интересуют средние времена перехода в каждый эр­годический класс, то систему уравнений (10.20) удобно записать в матричном виде. Обозначим , , .

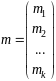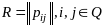Учитывая, что в этом случае 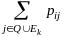=1, имеем 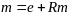, т.е. , где I - единичная матрица. Последнее соотношение и определяет вектор среднего времени перехода из несущественного состояния в эргодические классы.

Рассмотрим теперь среднее время перехода из состояния в состояние внутри класса. Пусть Е - множество состояний одного класса 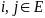. Через 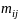обозначим среднее число шагов, необхо­димых для переходов из i -го состояния в j-е состояние. За один шаг цепь может из i -го состояния с вероятностью 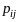перейти в j-е состояние, тогда время перехода будет равно 1, и оно будет равно 1 + m_kj, если за этот шаг цепь перейдет из i -го состояния в некоторое промежуточное k -е состояние. Тогда по формуле для условного мат. ожидания имеем 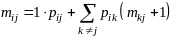или 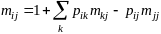.(10.21)

Введем матричные обозначения , , ,

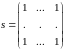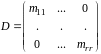где r - число состояний данного класса. Тогда систему ур-ний (10.21) можно переписать в матричном виде М = S + РМ -PD, откуда получаем 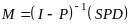. Эта формула определяет искомые средние значения времени пере­хода из одного состояния в другое. Выясним теперь, что собой представляют диагональные элемен­ты матрицы D. Для этого умножим систему уравнений (10.21) на финальную вероятность i-го состояния и просуммируем по i:

Тогда с учетом (10.17) имеем

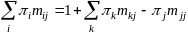
откуда находим .

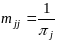41. Стационарные цепи Маркова

Всякое неотрицательное решение 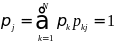, удовлет­воряющее условию нормировки, принято называть стационарным, или инвариантным, распределением вероятностей Марковской цепи с матрицей переходных вероятностей .

Опр. Набор чисел 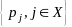называется стацио­нарным распределением цепи Маркова с дискретным време­нем, если:

1) является распределением вероятностей, т.е. .

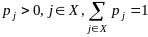2) 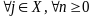имеет место равенство .

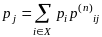В частности, если начальное распределение совпадает со стационарным, то на любом шаге цепь Маркова будет иметь стационарное распределение, поэтому такая цепь Маркова называется стационарной.

Т.1 (эргодическая теорема Маркова- Бернштейна). Если существуют такие и , что выполня­ется неравенство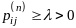 ,то цепь Маркова является эргодической; существует единственное стационарное распределение этой цепи, совпадающее с эргодическим.

Опр. Цепь Маркова с дискретным временем назы­вается неприводимой, если 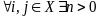такое, что .

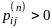Т.2 (эргодическая теорема Феллера). Неприводи­мая апериодическая цепь Маркова относится к одному из следую­щих двух классов:

а) все состояния цепи невозвратны (либо нулевые), в этом

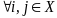
случае 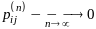, и не существует стационарного распределения цепи;

б) все состояния цепи положительны, в этом случае

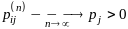при этом является стационарным распределением цепи и не существует других ее стационарных распределений.

Т.3 (эрг-кая т. Фостера). Для того чтобы неприводимая апериодическая цепь Маркова была эргодич-на, необходимо и достаточно, чтобы система уравнений 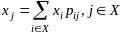имела нетривиальное решение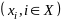 , такое, что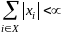 При этом существует единственное стационарное распределе­ние, которое совпадает с эргодическим.

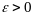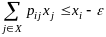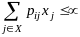Теорема 10.10 (эрг-кая т. Маркова). Для того, чтобы неприводимая апериодическая цепь Маркова была эргодична, достаточно существования , натурального числа i₀ и набора неотрицательных чисел х₀,х₁,х₂,... таких, что для , для .

При этом существует единственное стационарное распределе­ние, совпадающее с эргодическим.