54. Стохастический интеграл в форме Стратоновича

Пусть имеем разбиение интервала интегрирования точками а = t₁ < t₂ < …< t_n-1 = b. Рассмотрим интегральную сумму

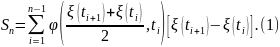
Если при существует предел в среднем квадратичном, то он называется стохастическим интегралом Стратоновича, или симметризованным стохастическим интегралом и обозначается (lim через точки)

.

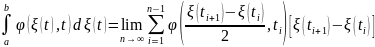Рассмотрим связь интегралов в форме Ито и в форме Стратоновича. Предположим, что функция 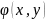диффиренцируема по первому аргументу. Используя разложение в ряд Тейлора в окрестности точки 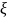(t_i), имеем:

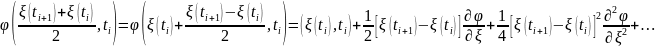
Подставляя это разложение в сумму (1) и переходя к пределу при , получаем (lim через точки)

55. Стохастические дифференциальные уравнения

Многие реальные объекты описываются дифференциальными уравнениями вида

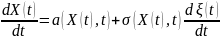(1)

или в форме дифференциалов (2)

Если - винеровский случайный процесс, то дифференциальное уравнение называется стохастическим. Стохастические дифференциальные уравнения принято обычно писать в форме дифференциалов, поскольку винеровский процесс является недифференцируемым.

Решение уравнений (1) и (2) определяется интегральным равенством

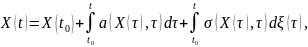(3)

где первый интеграл является стохастическим в среднеквадратичном смысле, второй интеграл является стохастическим в форме Ито или в форме Стратоновича, X(t₀) – значение процесса X(t) в начальный момент времени. Уравнение (3) называется стохастическим уравнением Ито.

Справедливо следующее утверждение.

Теорема. Пусть 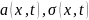– непрерывные по t функции и существует константа L, такая, что

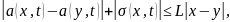
Тогда существует «единственное» решение уравнения (3) в том смысле, что

где Х₁(t), Х₂(t) некоторые решения уравнения (3).

Пусть а . Тогда решение уравнения (3), имеет вид

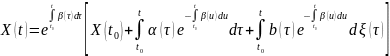(4)

Отсюда следует, что среднее значение данного решения можно записать в виде

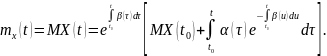
Покажем, что процесс Х(t), определяемый уравнением (3), является марковским. Действительно, распределение вероятностей Х(t) при t t₀ при заданном значении Х(t₀) зависит лишь от Х(t₀) и не зависит от прошлых значений Х(s), s < t_0, как видно из (3). А это является основным свойством марковского процесса. Поэтому процесс Х(t) полностью описывается коэффициентами сноса и диффузии. Пусть (t) – винеровский процесс с нулевым средним и единичным коэффициентом диффузии, второй интеграл в (3) будем понимать в форме Ито. Тогда

+ откуда после усреднения имеем т. е. а является коэффициентом сноса процесса Х(t). Найдем коэффициент диффузии. Используя (4), получаем

Отсюда, после усреднения будем иметь

таким образом, коэффициент диффузии процесса Х(t) равен

Знание коэффициентов сноса и диффузии позволяет записать уравнение Колмогорова – Фоккера – Планка для переходной плотности вероятностей, которая однозначно определяет поведение процесса Х(t). То есть, переходная плотность диффузионного случайного процесса Х(t) удовлетворяет уравнению Колмогорова – Фоккера – планка тогда и только тогда, когда случайный процесс Х(t) является решением стохастического дифференциального уравнения (2), в котором .