1.Решения

1. Решение на числовом промежутке

Решением на числовом промежутке Т системы 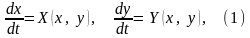называется векторная функция скалярного аргумента 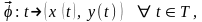относительно

которой выполняются условия:

1) функция дифференцируема;

2) точки (x(t),y(t)) ;

3) имеют место тождества

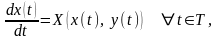
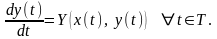
Если вектор-функция 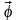есть решение на числовом промежутке Т системы (1), то она непрерывно дифференцируема на этом числовом промежутке: 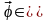С¹Т.

2. Задача Коши

Задача Коши с начальными данными (t₀, х₀,уо) состоит в нахождении векторов-функций (x(t),y(t)), определенных на некоторой окрестности U(to) точки to, которые являются решениями на U(to) системы (1) и при t = to принимают значение 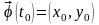, причем точка

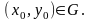
Функцию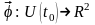 ,являющуюся решением задачи Коши с начальными данными (t₀,х₀,уо), обозначим

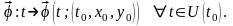
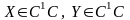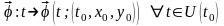Так как при для системы (1) выполняются условия теоремы Пикара — Линделефа, то решение задачи Коши системы (1) при любых начальных данных (to,xo,yo), лишь бы (хо,уо) 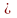G, существует и является единственным.

3. Продолжение решений.

Для решения системы (1) через 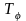обозначим числовой промежуток максимально возможного продолжения решения .

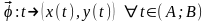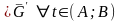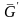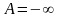Теорема 5.1 Если у системы (1) решение такое, что точки (x(t), y(t)) где — замыкание области , то , а .

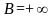4. Общее решение.

Непрерывная векторная функция векторного аргумента 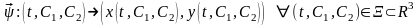(4.1)

называется общим решением систе­мы (1), если для любой фиксированной точки (х₀,уо) G при каждом фиксированном 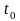система 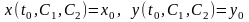имеет единственное решение , точка 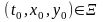вектор-функция есть решение задачи Коши с начальными данными системы (1).

(1) нет общих точек; через каждую точку (t, х, у) при (х, у) G G проходит одна интегральная кривая системы (1).

В каждой точке касательная к интегральной кривой системы (1) коллинеарна значению ассоциированного векторного поля (1.1) в этой точке, а направление значения векторного поля (1.1) указывает направление движения вдоль интегральной кривой.

ИНТЕГРАЛЫ

5. Интегральная поверхность

Гладкая поверхность координатного пространства Otxy называется интегральной поверхностью системы (1), если нормаль к этой поверхности в каждой ее точке ортогональна значению векторного поля в этой точке.

Расположение интегральных кривых системы (1) относительно интегральных поверхностей этой системы таково, что через каждую точку интегральной поверхности проходит одна интегральная кривая, причем интегральная кривая лежит на данной интегральной поверхности .

Теорема 9.1 Гладкая поверхность 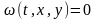является интегральной поверхностью системы (1) тогда и только тогда, когда (5.1) где функция такая, что 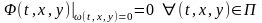(5.2)

6. Интегральная кривая, заданная неявно

Гладкая кривая, заданная неявно уравнениями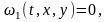 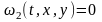, является интегральной кривой системы (1) тогда и только тогда, когда £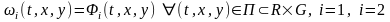 , причем

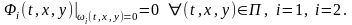
7. Первый интеграл

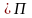
Непрерывная функция (7.1) называется первым интегралом на области системы (1), если эта функция сохраняет постоянное значение вдоль любого решения системы (1) такого, что точки (t, x(t), y(t)) , т.е. F(t,x(t),y(t)) = C , С - постоянная.

Теорема 7.1 Непрерывно дифференцируемая функция (7.1) является первым интегралом на области системы (1), если и только если ее дифференциал в силу системы (1) тождественно равен нулю на области , т.е. 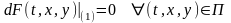(7.2) С помощью оператора 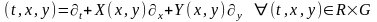тождество (7.2) записывается в виде 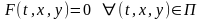(7.3)

Первый интеграл системы (1) имеет неоднозначное аналитическое задание.