
- •1.Решения
- •1. Решение на числовом промежутке
- •2. Задача Коши
- •3. Продолжение решений.
- •4. Общее решение.
- •5. Интегральная поверхность
- •6. Интегральная кривая, заданная неявно
- •7. Первый интеграл
- •8. Базис первых интегралов
- •2.Траектории
- •1. Траектория
- •3. Регулярные точки
- •4. Виды траекторий
- •5. Параметрическое задание траекторий
- •6. Неявное задание траекторий
- •7. Уравнение траекторий
- •7.Сложные состояния равновесия систем с линейными членами.
- •8. Признаки ограниченности числа предельных циклов.
- •10.Преобразование Бендиксона
- •13. Преобразование Пуанкаре.2
- •14. Круг Пуанкаре.
- •15. Типы диф. Сис-мы на проективной ф.П.
- •16. Поведение траекторий в окрестности экватора сферы Пуанкаре (s2 p)
- •17. Проективный атлас сферы Пуанкаре.
5. Параметрическое задание траекторий
Если
векторная ф-ция
яв-ся
общим решением с-мы (1), то траектории
с-мы (1) параметрически задаются ур-ями
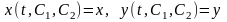 при
при
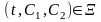
6. Неявное задание траекторий
Если
ф-ция
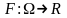 яв-тся
автономным первым интегралом на области
с-мы
(1), то семейство кривых
яв-тся
автономным первым интегралом на области
с-мы
(1), то семейство кривых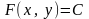 ,
где
,
где
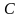 —
произвольная постоянная (случай С
= ±
не исключается), состоит из траекторий
с-мы (1).
—
произвольная постоянная (случай С
= ±
не исключается), состоит из траекторий
с-мы (1).
7. Уравнение траекторий
Уравнение
в дифференциалах
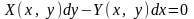 (7.1)
(7.1)
Наз-тся уравнением траекторий системы (1).
Ассоциированным уравнению (7.1) является плоское векторное поле .
Линейный
дифференциальный оператор первого
порядка
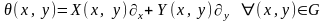 яв-ся оператором
дифференцирования в силу ур-ния (7.1).
яв-ся оператором
дифференцирования в силу ур-ния (7.1).
Траекториям с-мы (1) соответствуют траектории ур-ния (7.1), при этом СР с-мы (1) суть особые точки ур-ния (7.1).
Автономный
первый интеграл на области
системы
(1) есть общий интеграл на области
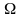 уравнения
(7.1), и, наоборот, общий интеграл на области
уравнения
(7.1) есть автономный первый интеграл на
области
системы
(1).
уравнения
(7.1), и, наоборот, общий интеграл на области
уравнения
(7.1) есть автономный первый интеграл на
области
системы
(1).
8. Изоклины
Кривая
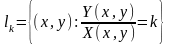 где
где
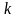 вещественное
число или
вещественное
число или
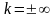 наз-тся
изоклиной
или
-изоклиной
уравнения
траекторий (7.1).
наз-тся
изоклиной
или
-изоклиной
уравнения
траекторий (7.1).
Траектории
системы (1) пересекают изоклину
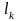 под
одним и тем же углом
под
одним и тем же углом
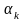 с
положительным направлением оси Ох
таким,
что
с
положительным направлением оси Ох
таким,
что
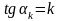
Теорема 8.1 Прямая, проходящая через два состояния равновесия системы (1), является изоклиной уравнения траекторий (7.1).
9. Контактные точки кривой
Точку,
в которой траектория системы (1) касается
кривой
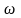 ,
лежащей
на фазовой плоскости Оху,
называется
контактной
точкой кривой
.
,
лежащей
на фазовой плоскости Оху,
называется
контактной
точкой кривой
.
Теорема 9.1. Каждая точка кривой является контактной тогда и только тогда, когда кривая суть траектория системы (1).
10. Контактные точки прямых
Теорема
10.1. Траектории
с-мы (1) касаются прямой
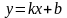 в
точках
в
точках
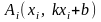 где
где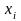 —такие
корни ур-ния
—такие
корни ур-ния
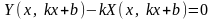 что
что
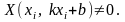
Теорема
10.2. Траектории
системы (1) касаются прямой
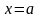 в
точках
в
точках
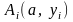 где
где
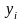 —
такие
корни уравнения
—
такие
корни уравнения
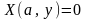 ,что
,что
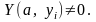
3. Простые состояния равновесия(СР)
Если
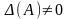 то
СР
то
СР
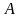 с-мы
(1) наз-ся простым.
с-мы
(1) наз-ся простым.
1. Направления примыкания
Траектории
с-мы (1) примыкают к простому состоянию
равновесия
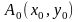 в
направлении прямых
в
направлении прямых
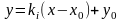 где
—
корни
уравнения
направлений примыкания
где
—
корни
уравнения
направлений примыкания
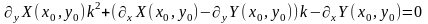 (1.1)
(1.1)
Если
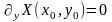 ,
то одним из корней ур-ния (1.1) считается
,
то одним из корней ур-ния (1.1) считается
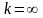 ,
а траектории с-мы (1) примыкают к простому
состоянию равновесию
в
направлении прямых, одна из которых
задается ур-ние
,
а траектории с-мы (1) примыкают к простому
состоянию равновесию
в
направлении прямых, одна из которых
задается ур-ние
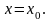
2. Седло
Если
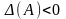 ,
то простое СР
яв-ся
седлом.
Траектории
седла А,
примыкающие
к нему, наз-ся сепаратрисами.
Простое
седло имеет четыре сепаратрисы, которые
разделяют четыре сектора Бендиксона.
Каждый сектор Бендиксона седла является
гиперболическим сектором.
,
то простое СР
яв-ся
седлом.
Траектории
седла А,
примыкающие
к нему, наз-ся сепаратрисами.
Простое
седло имеет четыре сепаратрисы, которые
разделяют четыре сектора Бендиксона.
Каждый сектор Бендиксона седла является
гиперболическим сектором.
3. Узел
СР
А
с-мы
(1) яв-ся узлом,
если выполняются условия
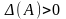 и
и
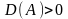 .
.
Все траектории узла примыкают к нему. Существенно то, что имеется два направления примыкания. В одном направлении примыкают две траектории, а в другом направлении примыкает пучок траекторий. Узел состоит из одного сектора Бендиксона, который яв-ся параболическим сектором.
4. Вырожденный узел
СР
с-мы
(1) яв-ся вырожденным
узлом если
,
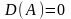 ,
,
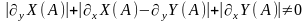 .
.
Все траектории вырожденного узла примыкают к нему в одном направлении. Вырожденный узел состоит из одного сектора Бендиксона, который яв-ся параболическим сектором.
5. Дикритический узел
Если
,
,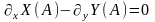 ,
,
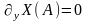 ,
,
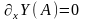 то СР
с-мы
(1) я-ся дикритическим
узлом.
то СР
с-мы
(1) я-ся дикритическим
узлом.
Все траектории дикритического узла примыкают к нему. У каждой траектории дикритического узла свое направление примыкания. Дикритический узел состоит из одного сектора Бендиксона, который яв-ся параболическим сектором.
6. Фокус
СР с-мы (1) я-тся фокусом, если выполняются условия ,
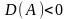 ,
,
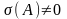
У фокуса нет направлений примыкания. Траектории фокуса ведут себя как спирали.
7. Центр
Если
,
,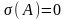 то СР
с-мы
(1) яв-ся фокусом или центром.
то СР
с-мы
(1) яв-ся фокусом или центром.
У центра нет направлений примыкания. Траекториями центра яв-ся замкнутые кривые, охватывающие его.
В случае, когда с-ма (1) яв-ся линейной, и выполняются условия , , ее СР А будет центром.
8. Грубые состояния равновесия
Простые СР типа седла, узла, вырожденного узла и дикритического узла, а также фокуса в случае, когда , , относятся к грубым состояниям равновесия .
Если , , то СР я-ся негрубым. Негрубое СР яв-ся фокусом или центром.
Пример:
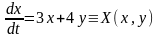
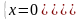
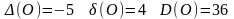
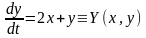 Значит
точка О(0,0)- седло
Пример2:
Значит
точка О(0,0)- седло
Пример2:
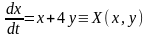
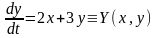 Значит
точка О(0,0)- седло
Значит
точка О(0,0)- седло
4.Простые состояния равновесия. Примеры систем с узлом.
34. Направления примыкания.
Траектории
с-мы
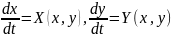 (1) примыкают
к простому СР
(1) примыкают
к простому СР
 в направлении прямых
в направлении прямых
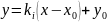 ,
где
,
где
 -корни
ур-ния
направлений примыкания
-корни
ур-ния
направлений примыкания
 (2)
(2)
Если
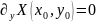 ,
то одним из корней ур-ния (2) считается
,
то одним из корней ур-ния (2) считается
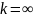 ,
а траектории с-мы (1) примыкают к простому
СР
в направлении прямых, одна из которых
задается ур-ем
,
а траектории с-мы (1) примыкают к простому
СР
в направлении прямых, одна из которых
задается ур-ем
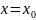 .
.
36. Узел
СР
А с-мы (1) яв-ся узлом,
если выполняются условия
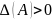 и
и
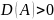 .
Все траектории узла примыкают к нему.
Существенно то, что имеется два направления
примыкания. В одном направлении примыкают
две траектории, а в другом – пучок
траекторий. Узел состоит из одного
сектора Бендиксона, который яв-ся
параболическим сектором.
.
Все траектории узла примыкают к нему.
Существенно то, что имеется два направления
примыкания. В одном направлении примыкают
две траектории, а в другом – пучок
траекторий. Узел состоит из одного
сектора Бендиксона, который яв-ся
параболическим сектором.
37. Вырожденный узел.
СР А с-мы (1) я-ся вырожденным узлом, если
,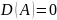 ,
,
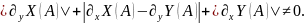
Все траектории вырожденного узла примыкают к нему в одном направлении. Вырожденный узел состоит из одного сектора Бендиксона, который является параболическим сектором.
38. Дикритический узел.
Если
,
,
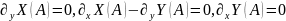 ,
то СР А с-мы (1) явл-ся дикритическим
узлом.
,
то СР А с-мы (1) явл-ся дикритическим
узлом.
Все траектории дикритического узла примыкают к нему. У каждой траектории дикритического узла свое направления примыкания. Дикритический узел состоит из одного сектора Бендиксона, который я-ся параболическим сектором.
39. Фокус
СР
А с-мы (1) явл-ся фокусом,
если вып-ся условия
,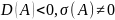 .
У фокуса нет направлений примыкания.
Траектории фокуса ведут себя как спирали.
.
У фокуса нет направлений примыкания.
Траектории фокуса ведут себя как спирали.
40. Центр
Если
,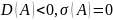 ,
то состояние равновесия А системы (1)
является фокусом или центром.
,
то состояние равновесия А системы (1)
является фокусом или центром.
У центра нет направлений примыкания. Траекториями центра являются замкнутые кривые, охватывающие его.
В случае, когда система (1) является линейной, и выполняются условия , , ее СР А будет центром.
Примеры систем с узлом:
СР
в конечной части фазовой пл-ти: О(0,0),
А(0,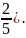
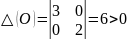
σ(О)=3+2=5>0
Д(О)=25-24=1>0
O(0,0) – неустойчивый узел
Состояние равновесия в конечной части фазовой плоскости: О(0,0)
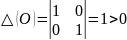
σ(О)=1+1=2>0
Д(О)=4-4=0 O(0,0) – дикритический узел
5.Простые состояния равновесия. Примеры систем с фокусом.
34. Направления примыкания.
Траектории с-мы (1) примыкают к простому СР в направлении прямых , где -корни ур-ния направлений примыкания
(2)
Если , то одним из корней ур-ния (2) считается , а траектории с-мы (1) примыкают к простому СР в направлении прямых, одна из которых задается ур-ем .
36. Узел
СР А с-мы (1) яв-ся узлом, если выполняются условия и . Все траектории узла примыкают к нему. Существенно то, что имеется два направления примыкания. В одном направлении примыкают две траектории, а в другом – пучок траекторий. Узел состоит из одного сектора Бендиксона, который яв-ся параболическим сектором.
37. Вырожденный узел.
СР А с-мы (1) я-ся вырожденным узлом, если
, ,
Все траектории вырожденного узла примыкают к нему в одном направлении. Вырожденный узел состоит из одного сектора Бендиксона, который является параболическим сектором.
38. Дикритический узел.
Если , , , то СР А с-мы (1) явл-ся дикритическим узлом.
Все траектории дикритического узла примыкают к нему. У каждой траектории дикритического узла свое направления примыкания. Дикритический узел состоит из одного сектора Бендиксона, который я-ся параболическим сектором.
39. Фокус
СР А с-мы (1) явл-ся фокусом, если вып-ся условия , . У фокуса нет направлений примыкания. Траектории фокуса ведут себя как спирали.
40. Центр
Если , , то состояние равновесия А системы (1) является фокусом или центром.
У центра нет направлений примыкания. Траекториями центра являются замкнутые кривые, охватывающие его.
В случае, когда система (1) является линейной, и выполняются условия , , ее СР А будет центром.
Примеры систем с фокусом:
1)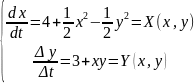
Состояния
равновесия в конечной части фазовой
плоскости: О(-1,3), А(1,-3
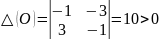
σ(О)=-1-1=-2<0
Д(О)=4-40=-36<0
O(0,0) – фокус
6. Простые состояния равновесия Примеры систем с центром.
34. Направления примыкания.
Траектории с-мы (1) примыкают к простому СР в направлении прямых , где -корни ур-ния направлений примыкания
(2)
Если , то одним из корней ур-ния (2) считается , а траектории с-мы (1) примыкают к простому СР в направлении прямых, одна из которых задается ур-ем .
36. Узел
СР А с-мы (1) яв-ся узлом, если выполняются условия и . Все траектории узла примыкают к нему. Существенно то, что имеется два направления примыкания. В одном направлении примыкают две траектории, а в другом – пучок траекторий. Узел состоит из одного сектора Бендиксона, который яв-ся параболическим сектором.
37. Вырожденный узел.
СР А с-мы (1) я-ся вырожденным узлом, если
, ,
Все траектории вырожденного узла примыкают к нему в одном направлении. Вырожденный узел состоит из одного сектора Бендиксона, который является параболическим сектором.
38. Дикритический узел.
Если , , , то СР А с-мы (1) явл-ся дикритическим узлом.
Все траектории дикритического узла примыкают к нему. У каждой траектории дикритического узла свое направления примыкания. Дикритический узел состоит из одного сектора Бендиксона, который я-ся параболическим сектором.
39. Фокус
СР А с-мы (1) явл-ся фокусом, если вып-ся условия , . У фокуса нет направлений примыкания. Траектории фокуса ведут себя как спирали.
40. Центр
Если , , то состояние равновесия А системы (1) является фокусом или центром.
У центра нет направлений примыкания. Траекториями центра являются замкнутые кривые, охватывающие его.
В случае, когда система (1) является линейной, и выполняются условия , , ее СР А будет центром.
Примеры систем с центром:
1)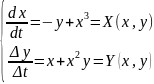
Состояние равновесия в конечной части фазовой плоскости: О(0,0)
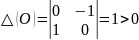
σ(О)=0+0=0
Д(О)==-4<0
O(0,0) – центр или фокус.


