10.Преобразование Бендиксона

Стереографическая проекция с центром в северном полюсе, посредством которого Ф. Пл-ть (x,y) отображается на сферу Бендиксона 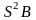обозначается .

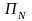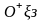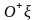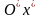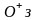На плоскости, касающейся в северном полюсе введем прямоугольную декартову систему координат так, чтобы ее начало координат совпадало с северным полюсом N, ось сонаправлена с осью , а ось с .

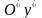Масштаб в прямоугольных декартовых системах координат 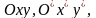одинаков.

Через 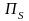обозначают стереографическую проекцию с центром в южном полюсе S при которой плоскость отображается на .

Если точка 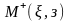в координатной плоскости , то в пространственной системе координат .

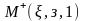Прямая 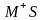задается системой .

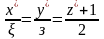Проекция является биективным отображением плоскости на проколотой в южном полюсе. Поэтому  обратное отображение 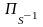, которое каждой точке , отличной от S, сопоставляет точку плоскости . Выполним последовательно два биективных отображения .

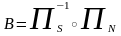Пусть дана произвольная точка плоск. (x,y) 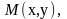ее образом при преобр. будет т. 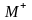плоск. .

.

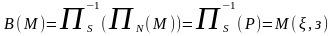Таким образом отобр. 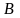устанавливает биективное отобр. ФП (x,y), проколотой в начале коорд. О, на плоск. проколотой в начале коорд. .

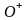Рассмотрим и обратное отобр. 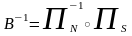, которое всякую т. ,отличную от начала коорд переводит в т. М ФП (x,y), отличную от начала коорд.

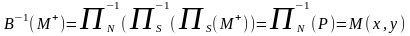
Пусть т. 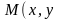), , 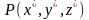таковы, что 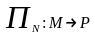, ,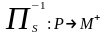тогда коорд. этих точек удовлетвор. системе уравнений:

.

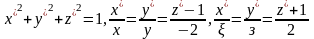Откуда получаем: .

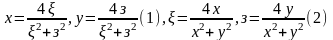ОПР:(1)– преобр. Бендиксона ФП(x,y), тогда (2)–обратное преобр. Бендиксона ФП(x,y).

Преобр. Бендиксона (1) устанавливает биективное отобр.

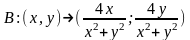
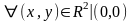(3)

в ФП(x,y),проколот. в начале коорд. О, на коорд.плоск. проколотой в .

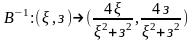
Аналогично обратное переоб. Бендиксона (2) устанавливает обратное отобр. Бендиксона 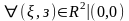(4)

в плоск. , проколотой в начале коорд. ,на плоск. (x,y),проколот. в О.

Заменой Бендиксона (1) дифф.систему 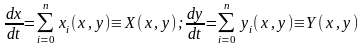(I) приводим к дифф.сист. 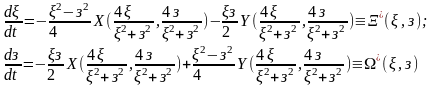(5), которая назыв. сист. Бендиксона индуцированная дифф. сист. (I).

Пусть X,Y-полиномы, тогда 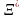и 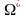не явл. полиномами, то (5) перепишется в виде 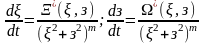(6), где и полиномы, которые не делятся одновременно на 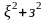, а m-целое неотрицател. число.

На основании (6) составим 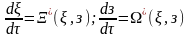(7), при .

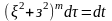ОПР:Относит. сист.(I) автономный. полином сист. (7) наз. В-приведенной сист.

При этом ФП В-привед.сист.

Связь между поведением траекторий сист.(I) на ФП (x,y) и поведением В-привед. сист. (7) на ФП .

1. Поведения траектор. дифф. сист. (7) в окрестности начала коорд. соотв. поведен. траектор. сист. (I) на в окр. северного полюса N. Тем самым по поведению траектор. приведенной сист. Бендиксона в окр. т. , устанавливается поведением траектор. сист. (I) на .

2. Если т. ) явл. Состоянием Равновесия сист.(I), которая расположена в конечной части ФП(x,y) и не совпадает с началом коорд. О(0,0), то т. 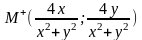будет СР сист.(7), при этом М и 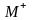одинакового вида. И наоборот: если т. явл. СР сист.(7), которая расположена в конечной части ФП и не совпадает с началом коорд. , то т. М будет такого же вида СР сист.(7).

3. При переходе от сист. (6) к сист. (7) в замене времени 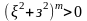. Поэтому направление движения вдоль соотв. траектор. сист. (I) и (7) одинаково. Сохраняется устойчивость СР как сист. (I) при отобр. Бендиксона (3), так и сист. (7) при обратном отобр. Бендиксона (4).

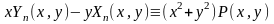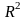Если выполняется условие на , где 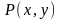– некоторый полином, то сист.(I) имеет неособый тип при преобр. Бендиксона и будем говорить, что сист.(I) В-неособого типа.В противном случае сист.(I) В-особого типа.

В сист. (I) В –неособого типа бесконечно-удаленная точка ФП явл. СР.

11в. Атлас сферы Бендиксона.

Поведение траекторий системы (I) будем изображать с помощью атласа, который состоит из двух карт K1(x,y), K2(ζ,ξ).

Плоскостью {(x*,y*,z*): z*=1-ε}, 0<ε≤1 сферу S^2 разобьем на две части:

S1={(X*,y*,z*): x*^2+y*^2+z*^2=1, 1≤z*≤1-ε},

S2={(X*,y*,z*): x*^2+y*^2+z*^2=1, 1-ε≤z*≤1}.

При этом число ε выберем так, чтобы на части S2 сферы Бендиксона не было образцов равновесия системы (I), расположенных в конечной части ее фазовой плоскости.

Карта K1(x,y) это круг, расположенный на фазовой плоскости (x,y) с центром в т О и являющийся прообразом части S1 сферы Бендиксона при стереографическом проектировании с центром в северном полюсе.

Карта K2(ζ,ξ) это круг, расположенный на фазовой плоскости (ζ,ξ) с центром в т O^+ и является прообразом части S2 сферы Бендиксона при стереографическом проектировании с центром в южном полюсе.

На карте K1(x,y) будут расположены все состояния равновесия системы (I) , отличные от ∞.

На карте K2(ζ,ξ) будут расположены не более одного состояния равновесия системы

dζ/dτ=Ξ(ζ,ξ), dξ/dτ=Ω(ζ,ξ), где (ζ^2+ξ^2)^mdτ=dt , которое расположено в точке O^+, т.е. на карте K2 изображается поведение траекторий системы (I) в окрестности бесконечно удаленной точки ее фазовой плоскости. То, что две карты K1(x,y) и K2(ζ,ξ) составляют атлас сферы Бендиксона, следует из свойства группы отображения Бендиксона.

Теорема: отображение Бендиксона B:(x,y)→(4x/x^2+y^2, 4y/x^2+y^2) для всех (x,y)єR^2\(0,0) и тождественное отображение фазовой плоскости на себя образуют группу второго порядка.

№ 12. Сфера Пуанкаре.

Относительно правой прямоугольной декартовой системы координат 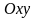фазовой плоскости 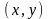системы

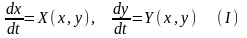
построим 3-х мерную прямоугольную декартову систему корд. с соблюдением следующих условий:

1. Прямая -ортогональна фазовой плоскости , и длина отрезка равна одной единице масштаба системы координат .

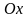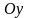2. Ось соноправлена с осью , ось соноправлена с осью , а ось 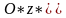направлена так, что система короодинат является правой.

3.Масштабы сиситемы координат и одинаковые.

Построрим единичную сферу с центром в точке .

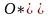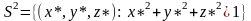(1)

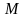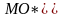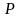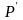На фазовой плоскости произвольным образом выберем точку и проведем луч с началом в точке через центр сферы . Этот луч пересекает сферу в двух диаметрально противоположных (антидиаметральных) точках и . Таким образом фазовой плоскости сопоставлено две диаметрально противопольжнее точки сферы, и обратно всякой паре диаметрально противопол. точек сферы, за исключением расположеной на экваторе сферы, соответствует одна точка фазовой плоскости .

Чтобы распостранить это соответствие на всю сферу условимся о следующем: бесконечно удаленную точку каждой прямой на фазовой плоскости , проходящую через начало координат будем считать бесконечно удаленной точкой фазовой плоскости . При этом на фазовой плоскости множество бесконечно удаленных точек явл. бесконечными, а разным кривым проходящих через точку 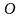соответствуют разные бесконечно удаленные точки фазовой плоскости . Множество таких бесконечно удаленных точек будем называть бесконечно удаленной частью фазовой плоскости. Таким образом фазовая плоскость состоит из двух частей: конечной и бесконечно удаленной.

Примем следующее соглашение:

Любые две диаметрально противоположные точки экватора соответствуют одной бесконечно удаленной точке фазовой плоскости , являющейся бесконечно удаленной точкой прямой фазовой плоскости которая проходит через естественные проекции точек экватора на фазовую плоскость .

Описанное соответствие позволяет проектировать траектории системы 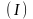на сферу 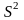, которую назовем сферой Пуанкаре и обозначается 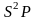. Поведение траекторий в бесконечно удаленной части фазовой плоскости определяет поведением их образов в окрестности экватора сферы Пуанкаре. Под поведением траекторий на сфере Пуанкаре подразумевается поведение образов траекторий на сфере Пуанкаре.

Закономерности поведения траекторий на сфере Пуанкаре.

1. Прямой на фазовой плоскости проходящей через начало координат сопоставляется меридиан на сфере. Прямая 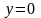отображается на начальный меридиан, а прямая 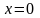на меридиан диагональный начальному.

2. Замкнутым линиям расположенным в конечной части фазовой плоскости сопоставляются две диаметрально противоположные замкнутые линии на сфере Пуанкаре не имеют общих точек с экватором. И наоборот, любым двум диаметрально противоположным замкнутым линиям на сфере Пуанкаре не имеющим общих точек с экватором, сопоставляется одна замкнутая линия, лежащая в фазовой плоскости.

3. Гиперболическому, параболическому, эллиптическому секторам Бендиксона некоторого состояния равновесия системы лежащей в конечной части фазовой плоскости соответственно сопоставляется по два диаметрально противоположных таким же секторам Бендиксона на сфере Пуанкаре. А центру и фокусу соответственно сопоставляются по два такого же вида. Таким образом на сфере Пуанкаре каждому состоянию равновесия системы 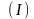из конечной части фазовой плоскости соответствует два диаметрально противоположных такого же вида состояния равновесия.

4. Направление движения вдоль траектории системы на фазовой плоскости относительно любого состояния равновесия при отображении на сохраняется относительно каждого из двух образов этого состояния равновесия, а направление движения вдоль траектории на относительно экватора соответствует направлению движения вдоль траекторий относительно бесконечно удаленной части фазовой плоскости. Устойчивость каждого состояния равновесия в конечной части фазовой плоскости, такая же как и у обоих его образов на сфере Пуанкаре. Пусть точка имеет координаты 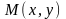в , тогда в получаем 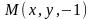. Прямая в имеет вид 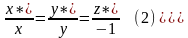. Точка отображается в точки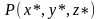 , 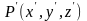. Точки и являются точками пересечения прямой и сферы , поэтому координаты этих точек явл. решением системы

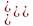Координаты точки выражаются через координаты точки

.
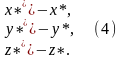