8. Базис первых интегралов

Теорема 8.1. Если функции

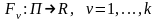
являются первыми интегралами на области 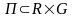системы (1), то функция , где 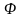- произвольная голоморфная функция, также будет первым интегралом на области системы (1).

В этой связи выделяются функционально независимые первые интегралы.

Совокупность функционально независимых на области первых интегралов системы (1) ; назовем базисом первых интегралов (или интегральным базисом) на области системы (1), если у этой системы любой первый интеграл 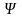на области можно представить в виде 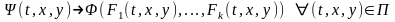, где — некоторая голоморфная функция. Число k при этом назовем размерностью базиса первых интегралов на области П системы (1).

Теорема 8.2 Системы (1) на окрестности любой точки из мно­жества 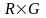имеет базис первых интегралов второй размерности.

Любые два функционально независимые на области первые интегралы системы (1) образуют интегральный базис на области П системы (1).

9. Общий интеграл

Если функции и образуют интегральный базис на области системы (1), а - произвольная непрерывно дифференцируемая функция, то функция 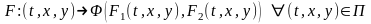называется общим интегралом на области П системы (1).

10. Неявное задание интегральных кривых

Если функции и образуют интегральный базис на области системы (1), то интегральные кривые системы (1) задаются неявно уравнениями

F₁(t,x,y) = C₁, F₂(t,x,y) = C₂, (10.1)

где C₁ и С₂ — произвольные постоянные или одна из бесконечностей ± .

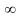11. Автономный первый интеграл

Первый интеграл системы(1)вида 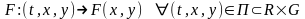(11.1)

называется автономным первым интегралом на, области П системы (1).

Автономный первый интеграл не зависит от независимой переменной t.

12. Последний множитель

Непрерывно дифференцируемую функцию 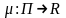назовем последним множителем на области системы (1), если

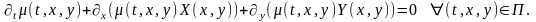(12.1)

С помощью оператора тождество (12.1) запишем в виде

(12.2)

Свойство Якоби : Есл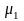и и 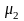— последние множители на области системы (1), то функция 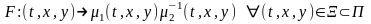является первым интегралом на области 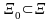системы (1).

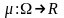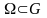Непрерывно дифференцируемую функцию назовем автономным последним множителем на области системы (1), если

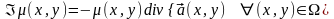(12.3)

2.Траектории

1. Траектория

Естественная проекция на ф. пл-ть интегральной кривой с-мы наз-ся траекторией этой с-мы.

_{Траектория} соответствующая решению параметрически задается уравнениями при

2.Состояние равновесия

Точка 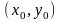ф. пл-ти Оху называется состоянием равновесия(СР) системы (1), если решение задачи Коши с начальными данными системы (1) продолжимо на всю числовую прямую и сохраняет постоянное значение .

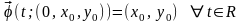СР с-мы (1) яв-ся естественной проекцией на ф. пл-ть интегральной прямой с-мы (1), параллельной оси Ot и проходящей через точку

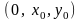
Теорема 2.1. Точка 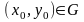яв-ся СР с-мы (1) тогда и только тогда, когда

3. Регулярные точки

Точки области G, которые не яв-тся СР с-мы (1), наз-ся регулярными точками этой с-мы.

Теорема 3.1. Точка яв-ся регулярной точкой с-мы (1), если и только если

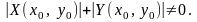
4. Виды траекторий

Теорема 4.1 Каждая траектория с-мы (1) принадлежит к одному из трех видов: 1) состояние равновесия; 2) замкнутая траектория, которой соответствует периодическое решение с положительным наименьшим периодом; 3) траектория без самопересечения, которой соответствует непериодическое решение.

В каждой точке траектории, отличной от состояния равновесия, системы (1) касательная к ней коллинеарна значению векторного поля (4.1) в этой точке, а на­правление значения векторного поля (4.1) указывает направление движения вдоль траектории.

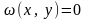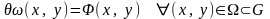
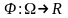Теорема 4.2. Гладкая кривая состоит из траекторий системы (1), если и только если где функция такая, что