1.Основные определения и свойства метрических пространств.

Опр: Пусть - произвольное множество и пусть любым двум элементам сопоставлено неотрицательное число , обладающее следующими св-ми, называющимися аксиомами метрики:

1. (аксиома отделимости);

2. , (аксиома симметрии);

3., (аксиома треугольника).

Тогда называется метрикой на множестве , а множество, на котором задана метрика, называется метрическим пространством.

Опр: Пусть Х ─ метрическое пространство с мерой ρ(x,y). Открытым шаром с центром в точке x₀ и радиусом r > 0 называется множество U(x₀,r)X.Точка x₀ наз-ся центром шара ,а R─радиусом шара.

Замкнутым шаром с центром в точке x0 радиуса r>0, наз-ся множество

Сферой с центром в x₀,радиуса R>0,называется множество S(x0,r)={xX | ρ(x,x₀)=r}.

Пусть MX , точка x₀M называется внутренней точкой , множества M, если существует U(x₀,r) M .

Любая точка открытого шара является внутренней точкой этого шара .

Совокупность всех точек множества M, называется внутренностью и обозначается M₀.

Множество M называется открытым ,если найдётся точка этого множества, которая является внутренней точкой ,т.е. MM₀ .

Множество M открыто тогда и только тогда ,когда оно совпадает со своей внутренностью.

2.Примеры метрических пространств.

Пример: Открытый шар.

Если точка Х принадлежит открытому множеству, то существует шар который содержится в данном множестве. Пустое множество этим свойством не обладает.

Совокупность всех открытых множеств открытого пространства X называется топологией этого пространства и обозначается r(x).

Обозначим через М^с ─ дополнение M (М^с =Х\M), М⁰ - внутренность, а М^с0 ─ внешность множества M.

Множество MX является замкнутым ,если дополнение М⁰ открыто.

3. Сходящиеся и фундаментальные последовательности в метрическом пространстве и их свойства.

Опр: Последовательность называется сходящейся последовательностью в метрическом пространстве , если расстояние .

Если последовательность сходится, то предел этой последовательности единственен.

Док-во:

Будем доказывать методом от противного. Пусть : , и являются пределами последовательности . Зафиксируем и возьмём . Так как последовательность сходится к , то выполняется (1). Т. К. явл. пределом послед-сти , то : (2), где 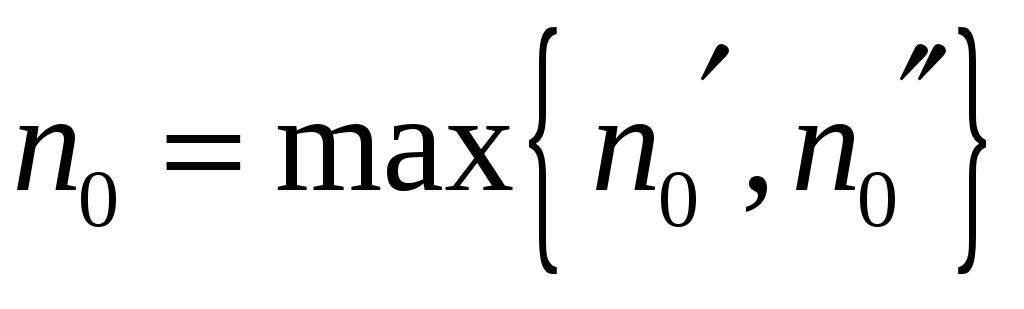. Так как выполняется (1) и (2), то , .

Опр: Последовательность в метрическом пространстве называется фундаментальной, если : .

Св-во: Если посл-сть сходится, то она фундаментальна.

Доказательство:

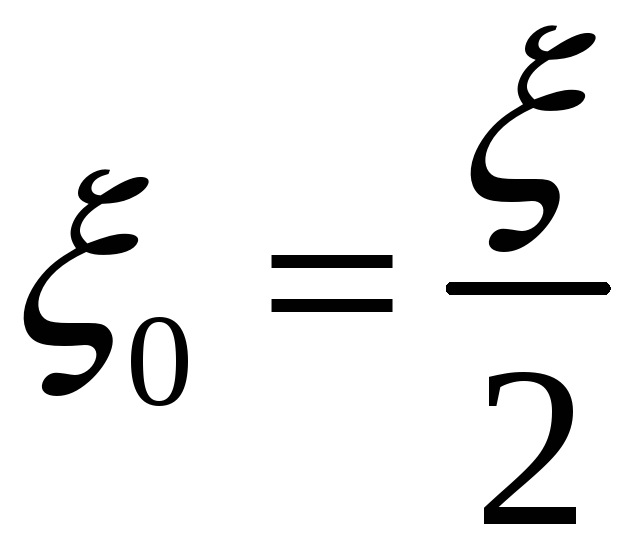Зафиксируем произвольное . Возьмём . Так как сходится, то : и : .

.

Опр: Метрическое пространство , в котором любая фундаментальная последовательность сходится, называется полным метрическим пространством.

Опр: Подмножество , - метрическое пространство, называется подпространством этого метрического пространства, если в введена метрика из метрического пространства , то есть , где - метрика и пара - подпространство метрического пространства с - индуцированной метрикой пространства .