
- •1.Основные определения и свойства метрических пространств.
- •3. Сходящиеся и фундаментальные последовательности в метрическом пространстве и их свойства.
- •4. Пространство и теорема о его полноте
- •5.Непрерывные отображения.
- •7. Принцип неподвижной точки.
- •10. Кольца и полукольца множеств.
- •13. Теорема (о кольце порожденном полукольцом )
- •18.Внешняя мера и ее св-ва
- •27.Ступенчатые ф-ции. Свойства ступ. Функций.
- •28. Интегрируемые ступенчатые функции и их св-ва
- •29.Интегралы от ступенчатой ф-ции
- •30.Измеримые ф-ции и их св-ва
- •35. Интегрируемые по Лебегу функции и их свойства
- •36. Определение интеграла Лебега. Корректность определения
- •43. Теорема (о прямом произведении полуколец).
- •44. Тензорное произведение мер
30.Измеримые ф-ции и их св-ва
Говорят, что
последовательность функций
![]() ,
заданных на множестве
,
заданных на множестве
![]() равномерно сходится к
равномерно сходится к
![]() ,
если
,
если
![]() .
.
В этом случае
пишут:
![]() .
.
Будем говорить,
что последовательность функций
![]() поточечно
сходится к функции
поточечно
сходится к функции![]() ,
если
,
если
![]() .
.
В этом случае
пишут:
![]() .
.
Определение.
Функция
![]() ,
определенная на множестве
,
определенная на множестве
![]() ,
называется измеримой, если существует
последовательность
,
называется измеримой, если существует
последовательность
![]() ступенчатых функций, которая равномерно
сходится к
ступенчатых функций, которая равномерно
сходится к
![]() на множестве
на множестве
![]() .
.
Совокупность всех
измеримых функций будем обозначать
![]() .
.
Свойства измеримых функций.
1. Произведение любого числа на измеримую функцию есть измеримая функция, т.е.
![]() .
.
Действительно,
т.к.
![]() .
Умножим обе части соотношения на
.
Умножим обе части соотношения на![]() ,
получим
,
получим
![]() .
По свойству 1 ступенчатых функций
.
По свойству 1 ступенчатых функций
![]() .
.
2.
Сумма двух измеримых функций является
измеримой функцией, т.е.
![]() .
.
Действительно,
т.к.
![]() ,
то
,
то
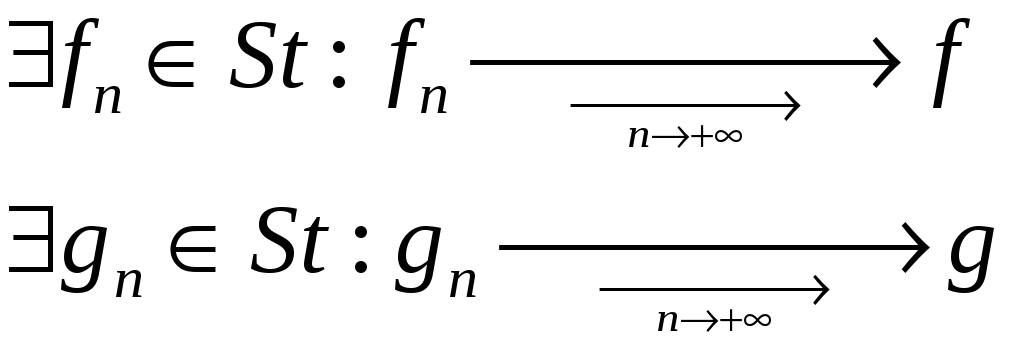
Суммируя эти соотношения, получаем:
![]() .
.
По свойству 2
ступенчатых функций
![]() .
.
3. Линейная комбинация измеримых функций является измеримой функцией, т.е.
![]() .
.
Доказательство следует из свойств 1 и 2.
Это свойство
значит, что совокупность всех измеримых
функций образует векторное (линейное)
пространство над полем
![]() .
.
4. Произведение измеримых функций является измеримой функцией, т.е.

5.
Если
![]() ,
то модуль измеримой функции является
измеримой функцией, т.е.
,
то модуль измеримой функции является
измеримой функцией, т.е.
![]() .
.
Действительно,

Определение.
Пусть функция
![]() определим
множество
определим
множество
![]() -
Лебеговское множество.
-
Лебеговское множество.
Замечание. Любая непрерывная ф-ция явл измеримой.
31.
32.
33.
34. Сходимость почти всюду. Канторово мн-во.
Определение.
Будем говорить, что некоторое свойство
![]() выполняется почти всюду на множестве
выполняется почти всюду на множестве
![]() ,
если
,
если
![]() свойство
свойство
![]() выполняется. Пример.
выполняется. Пример.
![]() ,
так как в качестве
,
так как в качестве
![]() ,
,
![]()
![]() ,
если
,
если![]() .
.
Определение.
Функции
![]() называются эквивалентными, если они
почти всюду равны, то есть
называются эквивалентными, если они
почти всюду равны, то есть
![]() .
.
Определение.
Последовательность
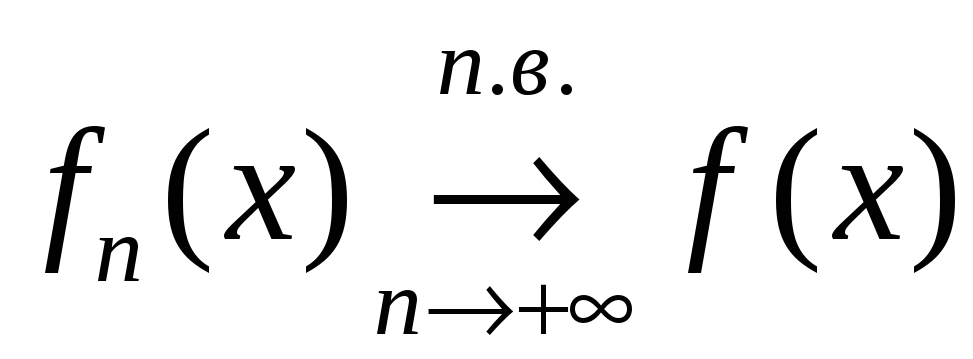 ,
если
,
если
![]()
![]()
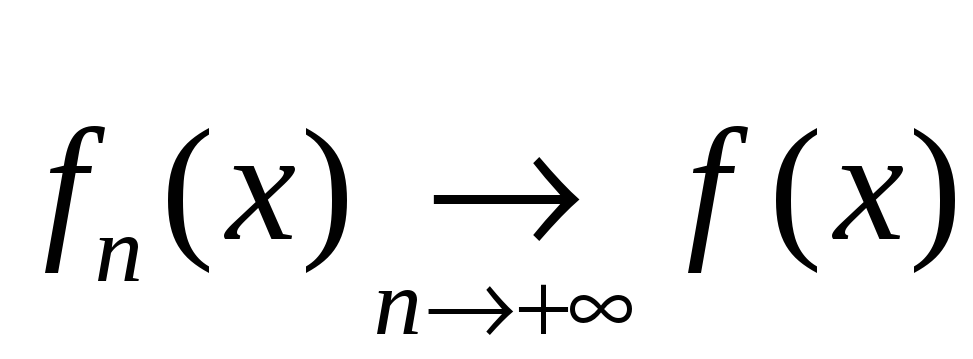 .
.
Теорема (о
сходящейся почти всюду последовательности
измеримых функций). Если
последовательность измеримых функций
 ,
то функция
,
то функция
![]() измерима.
измерима.
Для канонической меры: мера любого канонического множества (т.е. точки) равна 0.
Замечание.
Пусть
![]() счетное мн-во. Тогда
счетное мн-во. Тогда
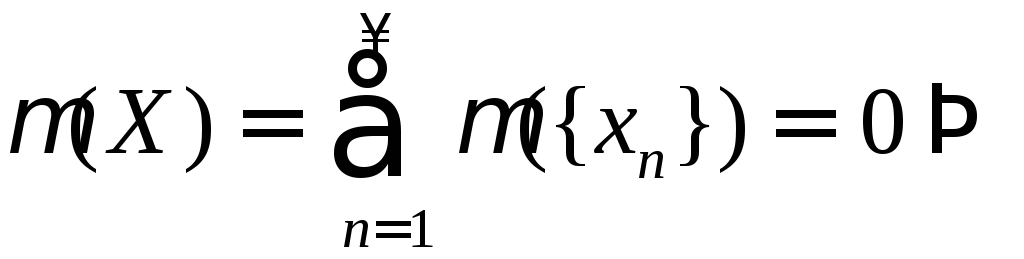 мера всех рациональных точек на
прямой будет также равна 0, т.е. (Q)=0,
т.к. Q-счетное
мн-во.
мера всех рациональных точек на
прямой будет также равна 0, т.е. (Q)=0,
т.к. Q-счетное
мн-во.
Рассмотрим Канторово мн-во.
Выбрасываем середину. Имеем [0;1/3]U[2/3;1] . Каждый из [0;1/3] и [2/3;1] делим на 3 части и выбрасываем середину. Получаем 4 отрезка и т.д.
Получили в итоге
![]()
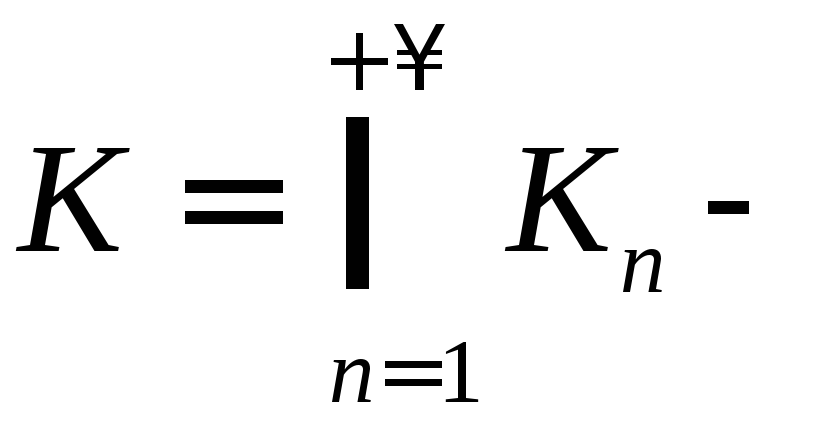 замкнутое
ограниченное мн-во. Оно явл-ся компактом.
И наз-ся канторовым мн-вом.
замкнутое
ограниченное мн-во. Оно явл-ся компактом.
И наз-ся канторовым мн-вом.
Посчитаем меру канторового мн-ва. Для этого посчитаем меру выброшенных интегралов.
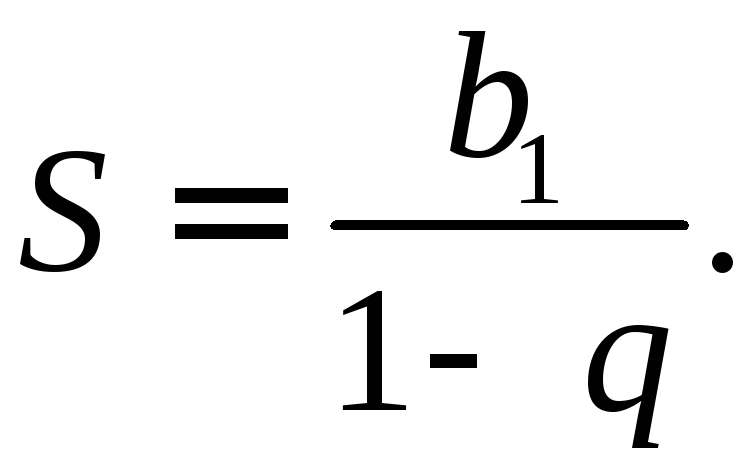

Следовательно из отрезка [0;1] длиной 1-0=1 выбросили сумму длин интервалов длиной 1.
По св-ву аддитивности ([0;1])=(M)=(K)(K)=0
