7. Принцип неподвижной точки.

Опр.: если имеем отображение F: XX, то точка аХ называется неподвижной точкой отображения, если Fa=а.

Теорема (принцип неподвижной точки)

Пусть F – сжимающее отображение полного метрического пространства Х, тогда существует единственная неподвижная точка у отображения F.

Доказательство:

Возьмем произвольную точку х₀ Х и построим точку

х₁= F х₀,

х₂ = (FF)х₀ = F² х₀,

х₃ = F х₂ =( FF²)х₀ = F³ х₀,

…………………………….

x_n = F х_n-1 =( FF ^n-1)х₀ = Fⁿ х₀

…………………………….

Получили последовательность

Докажем, что эта последовательность фундаментальна.

Возьмем 2 натуральных числа n,m, будем считать, что m n, тогда запишем m=р+n, р. Рассмотрим расстояние (x_n,x_m) =(Fx_n-1,Fx_m-1)q(x_n-1,x_m-1) =0<q<1=q(Fx_n-2,Fx_m-2) q²(x_n-2,x_m-2) qⁿ(x₀,x_m-n)= qⁿ(x₀,x_-p)

Так. обр., доказали нер-тво (x_n,x_m) qⁿ(x₀,x_-p) (3)

Рассмотрим (x₀,x_-p) и применим неравенство треугольника:

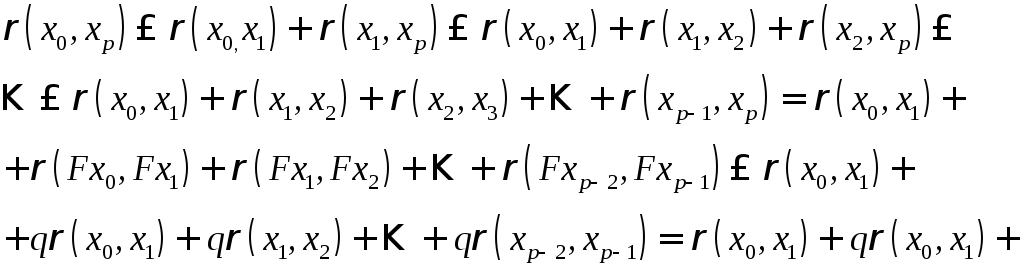
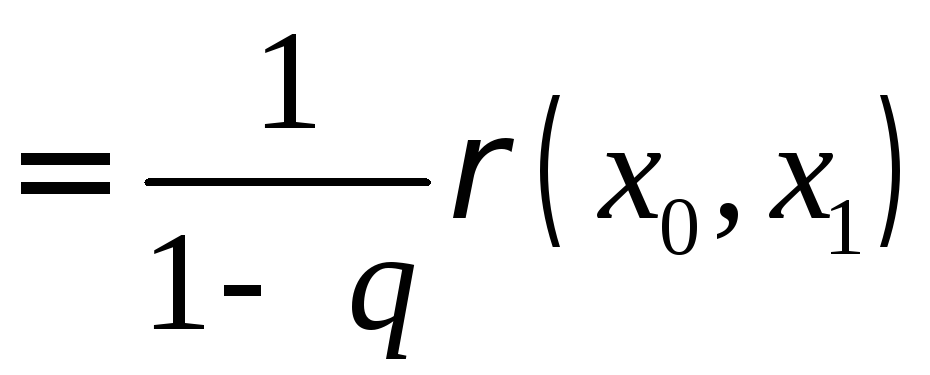
Таким образом доказали неравенство:

(4)

Из (3) и (4) получаем (5)

Рассмотрим правую часть (5). Так как q<1, то , следовательно, вся правая часть .

Это значит, что (6)

Т.к. m>n , то соотношение (6) верно и для .

Таким образом получаем:

.

А эта формула означает, что посл-ть явл. фунд-ной посл-стью в метрическом пространстве Х. В силу условия теоремы о том, что метрическое пространство полное, получаем, что последовательность явл. сходящейся последовательностью, т.е. существует такой элемент .

Рассмотрим рав-во , которое верно для (7)

Т.к. отображение F по условию теоремы сжимающее, то оно непрерывно и, следовательно, получаем

Переходя в общих частях равенства (6) к пределу при , получаем в пределе х*=Fx*, т.е. x*- неподвижная точка отображения F.

8.

9.

10. Кольца и полукольца множеств.

Определение : совокупность подмножеств множества X называется кольцом если:

1)

2)

Кольцо обладает следующими свойствами:

т.к.

Кольца содержащие X называются алгеброй .

Множества A и B непересекающиеся если . Система множеств -- является непересекающейся если элементы попарно не пересекаются т.е. для таких что . Будем обозначать пересечение непересекающихся мн-тв A и B.

Пусть X – множество , A ,B , C и -- подмножества множества X. Совокупность всех подмножеств . А также на X введены операции :

Объединение

Пересечение

Разность A\B

Симметрическая разность

Опр: Система подмножеств S множества X называется полукольцом если:

1)

2) ,

11. Примеры полуколец и колец.

Примеры:

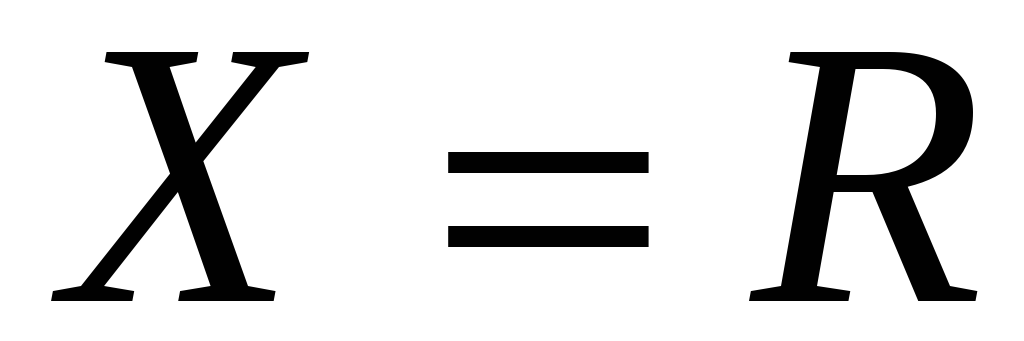1. Пусть и 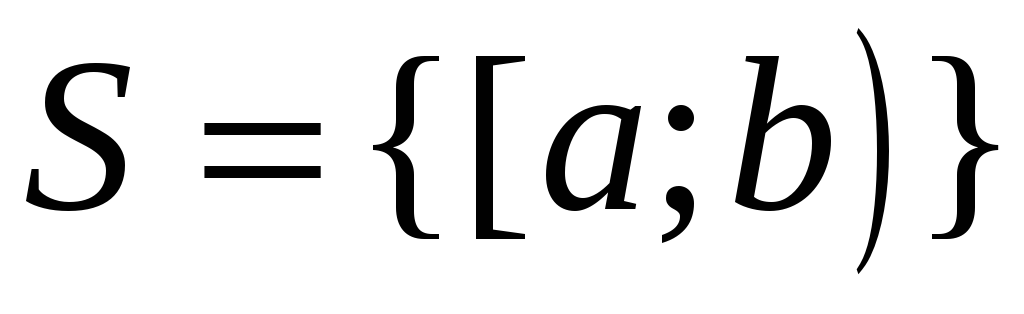. Пересечение полуинтервалов – полуинтервал . Множество полуинтервалов образуют полукольцо.

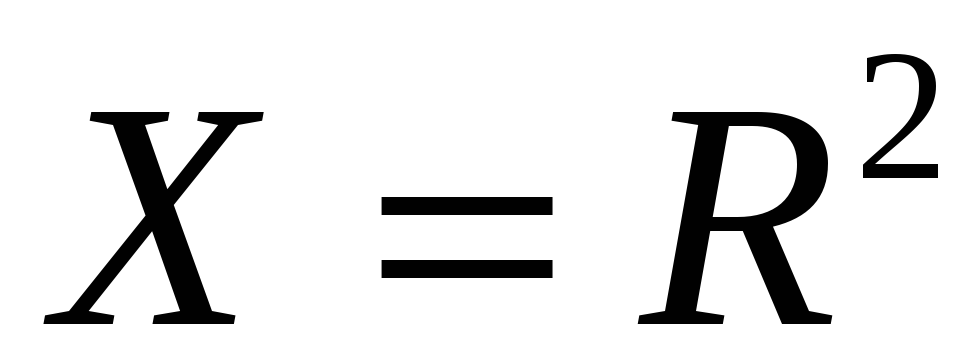2. Пусть и

12.