
- •1.Основные определения и свойства метрических пространств.
- •3. Сходящиеся и фундаментальные последовательности в метрическом пространстве и их свойства.
- •4. Пространство и теорема о его полноте
- •5.Непрерывные отображения.
- •7. Принцип неподвижной точки.
- •10. Кольца и полукольца множеств.
- •13. Теорема (о кольце порожденном полукольцом )
- •18.Внешняя мера и ее св-ва
- •27.Ступенчатые ф-ции. Свойства ступ. Функций.
- •28. Интегрируемые ступенчатые функции и их св-ва
- •29.Интегралы от ступенчатой ф-ции
- •30.Измеримые ф-ции и их св-ва
- •35. Интегрируемые по Лебегу функции и их свойства
- •36. Определение интеграла Лебега. Корректность определения
- •43. Теорема (о прямом произведении полуколец).
- •44. Тензорное произведение мер
13. Теорема (о кольце порожденном полукольцом )
Если S – полукольцо то K(s) – кольцо .
Док-во
Пусть
![]() ,
,
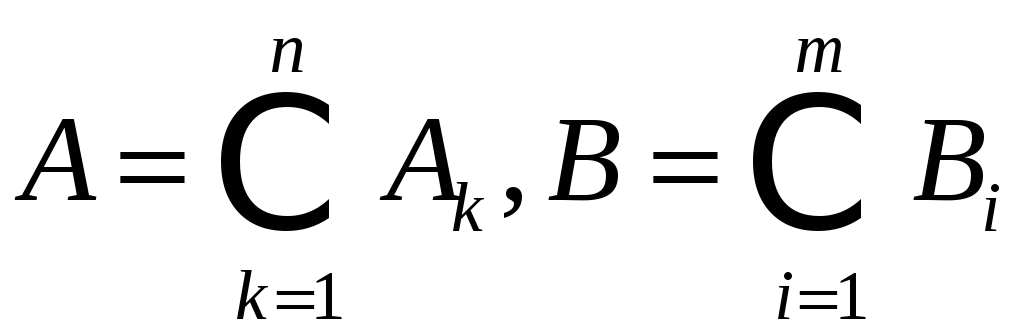 где
где
![]()
Рассмотрим
![]() и покажем что
и покажем что
![]()
I.
![]() ,
,
![]() покажем что
покажем что

Будем доказывать методом мат. индукции (индукцию проводим по n):
-
n=1
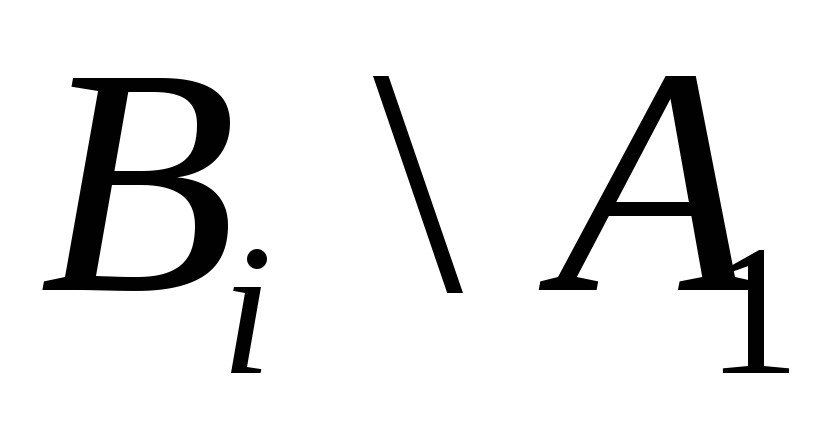
 где
где
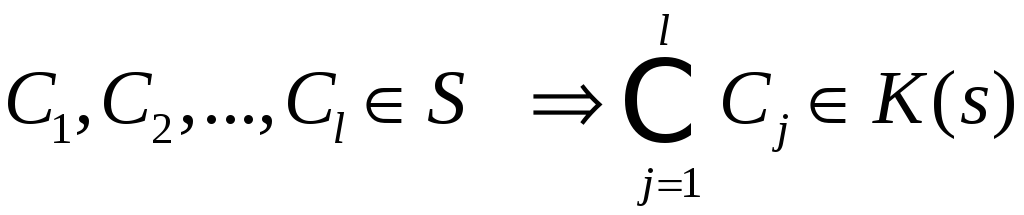
-
Пусть наше утверждение верно при n-1 т.е.
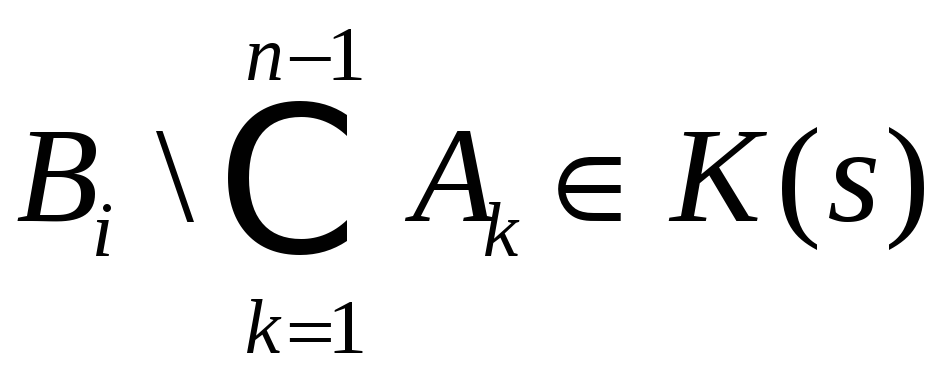
покажем что оно справедливо и для n:
 тогда можно
записать:
тогда можно
записать:
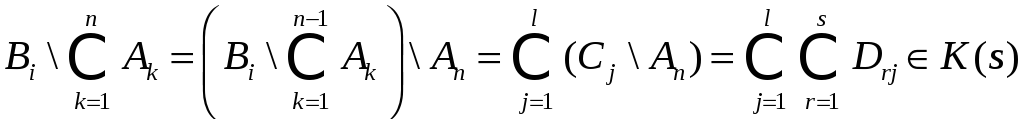
т.о. можно записать
![]() из
из
![]() справедливо :
справедливо :

I
I.
Тогда
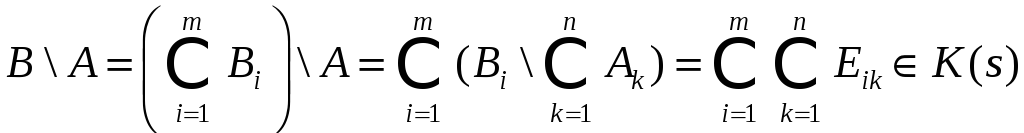
Т.о. показано что
![]()
![]()
Тогда :
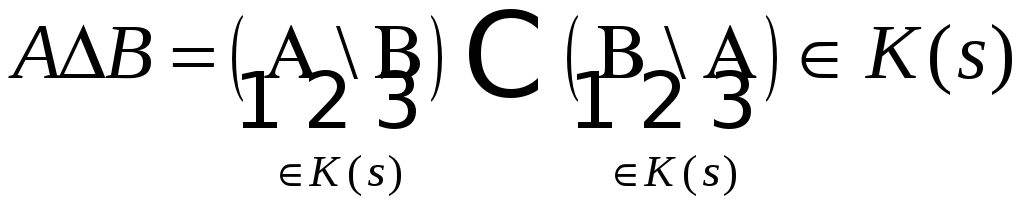

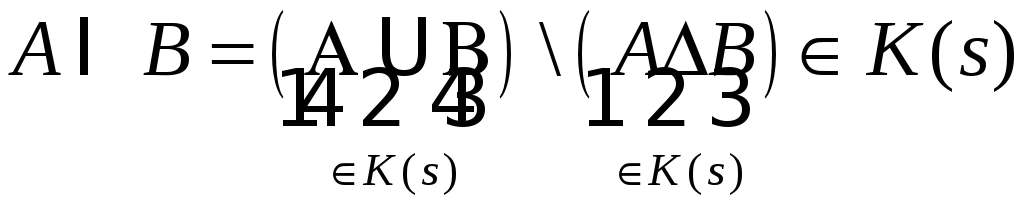
Мы доказали что
![]() и :
и :
 -- кольцо.
-- кольцо.
![]()
множества которые принадлежат K(s) называются элементарными множествами.
14. Теорема о распространении мера с полукольца на кольцо
Пусть мера
задана на полукольце
![]() , тогда мера
единственным образом распространяется
на порождаемое кольцо К(
, тогда мера
единственным образом распространяется
на порождаемое кольцо К(![]() ),
а именно
),
а именно

![]() (1)
(1)
Д-во:
Для
![]() возьмем
возьмем
![]() ,
тогда
,
тогда
![]() ,
,
где
![]() - распространение (расширение) прежней
меры
- распространение (расширение) прежней
меры
![]()
Если
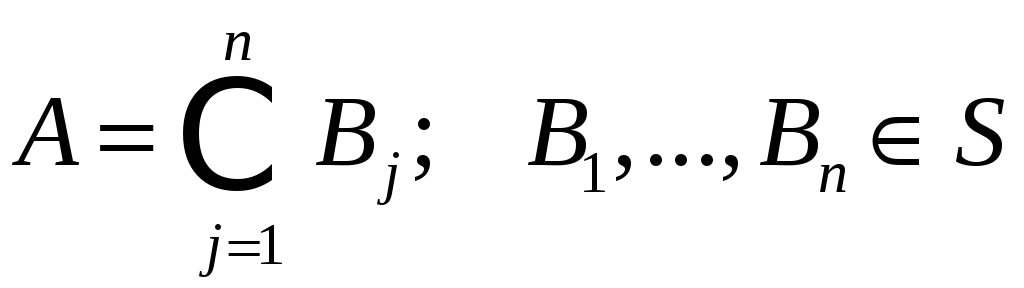 ,
то по (1) получаем
,
то по (1) получаем
![]() (2)
(2)
Определение, которое дается формулой (1), корректно, т.к. правые части (1) и (2) равны. Проверим это.
Введем обозначение
![]() ,
,
![]() .
Части
.
Части
![]() не пересекаются. Рассмотрим
не пересекаются. Рассмотрим

Рассмотрим правую часть (1), т.е.

Таким образом, мы доказали, что правые части (1) и (2) равны.
Будем говорить,
что
![]() - мера на кольце K(S).
Докажем, что эта мера неотрицательна и
аддитивна.
- мера на кольце K(S).
Докажем, что эта мера неотрицательна и
аддитивна.
Доказательство.
-
То, что она неотрицательна
 из (1) как сумма неотрицательных чисел,
из (1) как сумма неотрицательных чисел,

-

Докажем это.
![]()
![]()
![]()
Т.к. по условию
![]() ,
то их части тоже не пересекаются, т.е.
,
то их части тоже не пересекаются, т.е.
![]()

т.е.
![]() - мера на кольце
- мера на кольце
![]() (является расширением первоначальной
меры на
(является расширением первоначальной
меры на
![]() ).
).
15.
16. σ – аддитивные меры и их свойства
Определение.
Мера
![]() ,
заданная на
,
заданная на
![]() ,
называется
,
называется
![]() - аддитивной, если
- аддитивной, если
![]() ;
причем
;
причем
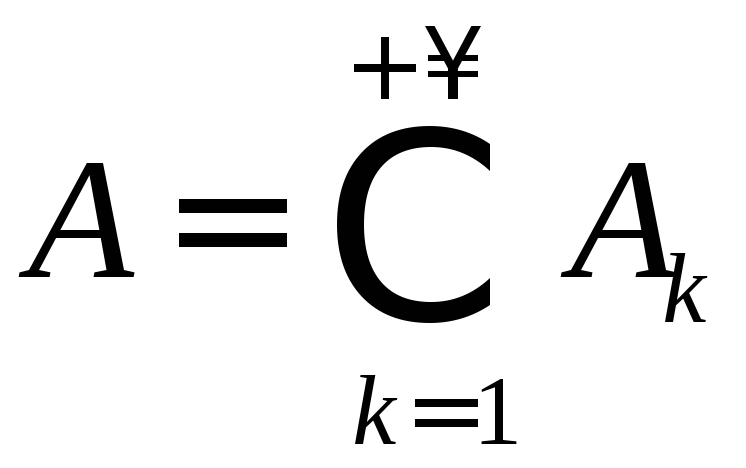 ,
то
,
то
![]() .
.
![]() ,
возьмем точку
,
возьмем точку
![]() и определим меру
и определим меру
![]() :
:

Тогда
![]() называется атамарной мерой, сосредоточенной
в точке
называется атамарной мерой, сосредоточенной
в точке
![]() .
.
Покажем, что это мера. Проверим аксиомы.
-
Неотрицательность следует из определения, т.е.

-
Проверим выполнение условия аддитивности.
![]()
Докажем, что
![]()
-
Пусть
 ,
тогда
,
тогда
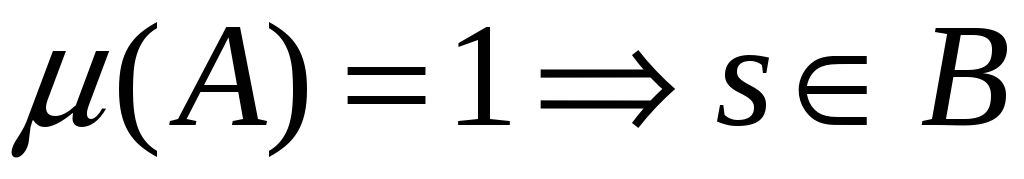 или
или
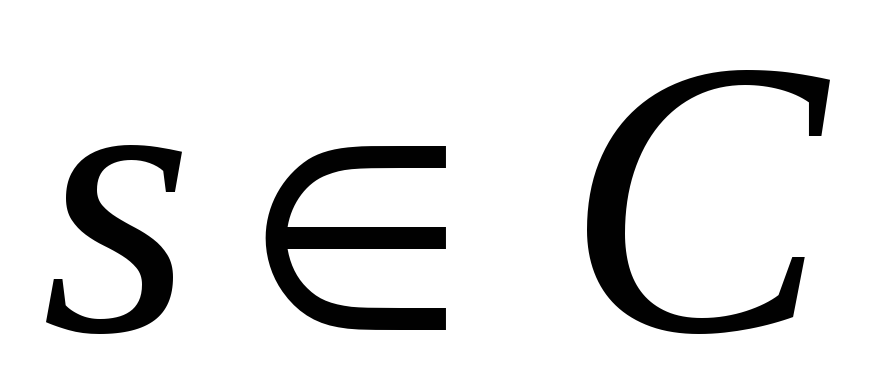 .
.
Пусть
![]() ,
тогда
,
тогда
![]() и
и
![]() .
В противном случае получаем
.
В противном случае получаем
![]() и
и
![]() или
или
![]() .
.
-
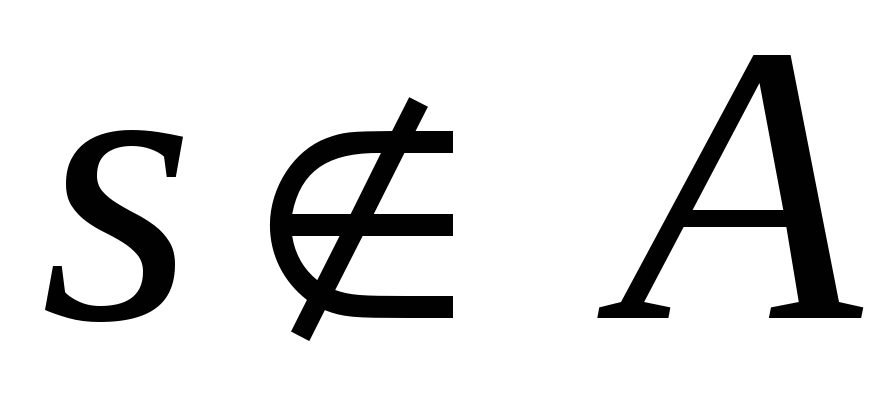 ,
тогда
,
тогда
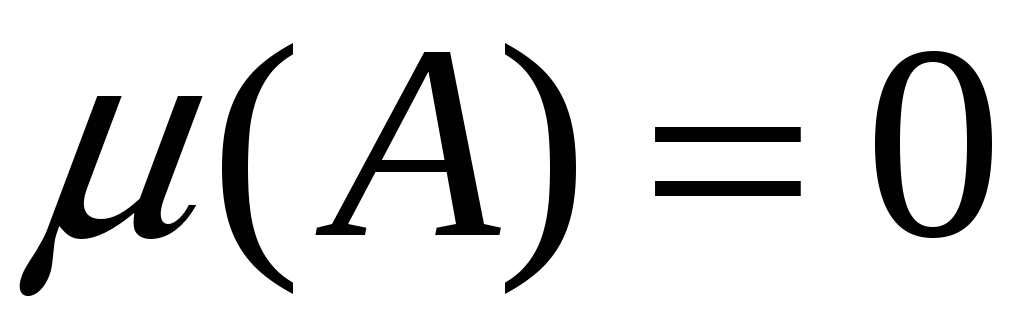 ,
но
,
но
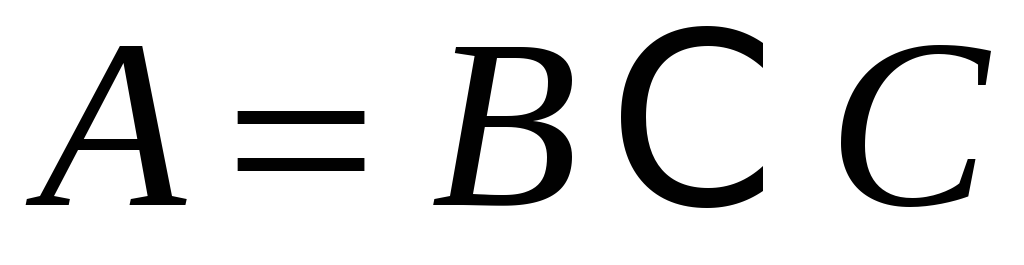 ,
значит, т.к.
,
значит, т.к.
 ,
то
,
то
 и
и
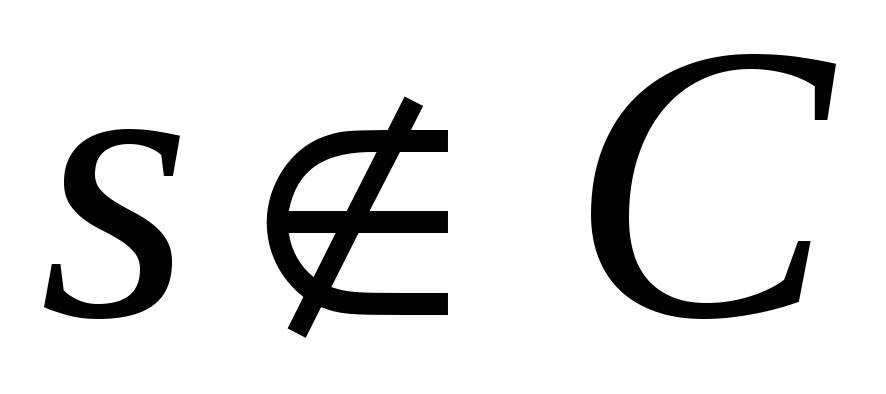 ,
то
,
то
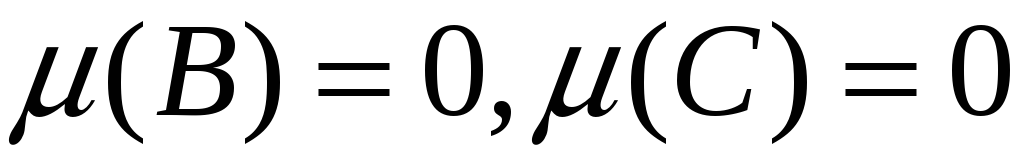 .
.
![]() является мерой.
является мерой.
Пусть
 .Докажем,
что
.Докажем,
что
![]() -аддитивная
мера.
-аддитивная
мера.
Для доказательства необходимо рассмотреть два случая:
1)
![]()
![]() верно равенство
верно равенство
![]()
2)
![]()
![]() верно равенство
верно равенство
![]()
Доказали, что любая
атамарная мера является
![]() -аддитивной
мерой.
-аддитивной
мерой.
17.
