4. Пространство и теорема о его полноте

- пространство всех непрерывных функций на отрезке . - Чебышевская метрика.

Докажем, что функция действительно является метрикой:

1) , то есть :

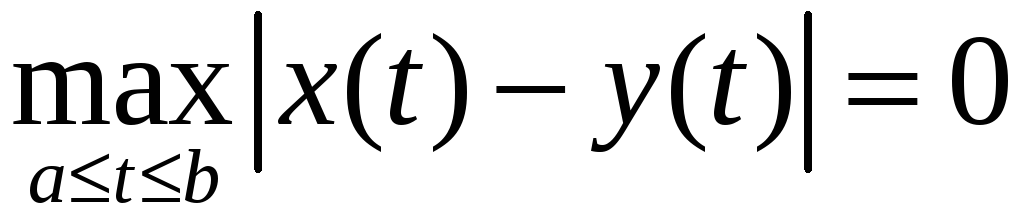
2)

3) : , ,

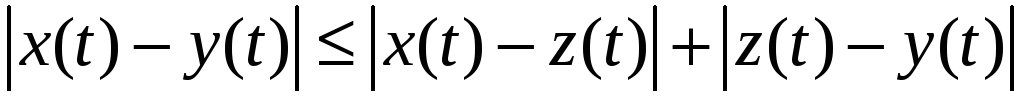Теорема (о полноте). Пространство полное.

Док-во. Пусть-фундаментальная последовательность в пространстве С[a,b], т.е. .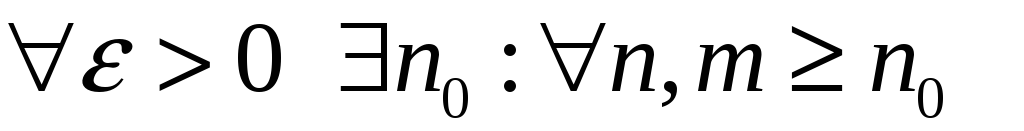

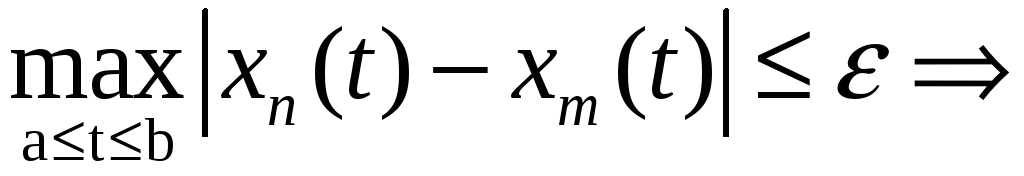
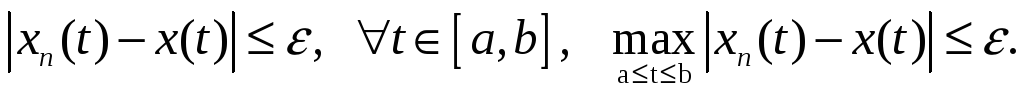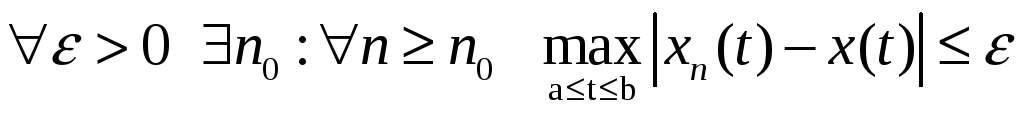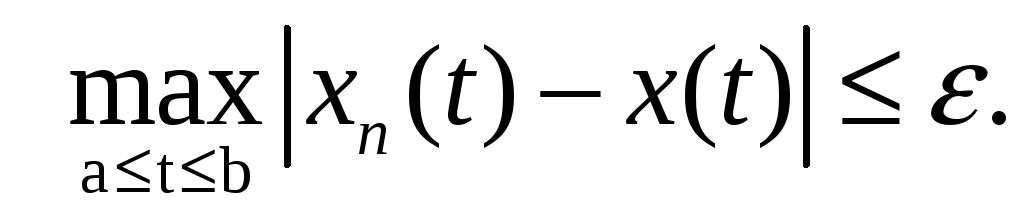
Это зн., что посл-ть яв-ся фундаментальной  существует, в силу полноты, . Т.к. это верно для любого t, то м. построить ф-цию ф-ция сходится поточечно. Получаем Т.о., , функция x(t) непрерывна на , а т.к. сходимость равномерная, то в

С[a,b]  С[a,b] – полное пр-во.

5.Непрерывные отображения.

Рассмотрим два метрические пространства X и Y с метрикой ρ_x и ρ_y .Отображение F:X→Y(т.е. каждому x X сопоставляем единственный yY, xX→ y Y, y=F(x)=Fx.

Опр.: Отображение F называется непрерывным в точке aX, если ε>0, δ>0 такое ,что если ρ_x(x,a)< δ , то ρ_y(F(x),F(a))< ε.

Отображение является непрерывным , если оно непрерывно в каждой точке. Тогда предыдущее определение можно записать следующим образом:

Теорема (Об эквивалентном условии непрерывности):

Для того чтобы отображение F было бы непрерывным в точке aX необходимо и достаточно , чтобы для любой последовательности .

Доказательство:

1) Необходимость. Пусть отображение F непрерывно в точке

a , т.е. ε>0, δ>0 ,что FU(a, δ) V(Fa, ε) (1).

Возьмём произвольную посл-сть , которая стремится к a , .

. Т.е. δ>0 n₀ ,что n≥ n₀ ρ(x_n,a)< δ (2).

А это значит ,что x_n U(a, δ). Из соотношений (1) и (2) получим , что F(x_n)V(F(a), ε).А это означает , что расстояние ρ_y(F(x),F(a))< ε.

Т.о. ε>0 n₀ , что n≥ n₀ выполняется ρ_y(F(x_n),F(a))< ε. А это означает ,что F(x_n) сходится к F(a) , .

2) Достаточность. Пусть выполняется условие (*). Докажем, что отображение F непрерывно.

Будем предполагать , что условие (*) выполняется , но F непрерывно в точке a .Это значит ,что ε>0, δ>0, ρ_x(x,a)< δ, но ρ_y(F(x),F(a))≥ ε.

Возьмём δ=1/n , тогда существует x_n ,что хотя ρ_x(x,a)<1/n= δ, но ρ_y(F(x),F(a))≥ ε. Следовательно из условия ρ_x(x_n,a)<1/n .А из условия ρ_y(F(x),F(a))≥ ε следует , что не стремится к при .Что противоречиво условию(*).

Получено противоречие показывает , что наше допущение не верно. Значит отображение F непрерывно в точке a .

Если отображение F непрерывно в каждой точке aMX , то говорят , что отображение F непрерывно на множестве M .

Отображение F непрерывное на всём пространстве Х называется непрерывным отображением .

Множество всех непрерывных отображений из X в Y обозначим C(X,Y).

Теорема: (О непрерывности композиции).

Пусть F непрерывное отображение F:X→Y , а G: Y→Z , где X,Y,Z –метрические пространства. Тогда композиция отображений G°F(которая определяется следующим образом (G°F)(x)=G(Fx) xX) является непрерывным отображением G°F:X→Z.

(Кратко: композиция непрерывных отображений является непрерывным отображением).

Доказательство:

Возьмём произвольное aX и пусть , тогда применяя теорему об эквивалентных условиях непрерывности мы получим .И еще раз её применяя, получим ,что . Т.е. это означает , что (G°F)(x_n)= (G°F)a (3)

Ещё раз применяя предыдущую теорему получаем , что G°F непрерывно в a ,т.е. G°F непрерывна.

Теорема доказана.

6. Сжимающие отображения.

Будем рассматривать отображение F: XУ с метрикой .

Определение: отображение F: XУ с метрикой  называется сжимающим отображением (отображением сжатия), если существует число 0<α<1, что расстояние между образами

_у(Fx₁ ,Fх₂) α_х(x₁,х₂),  х₁,х₂ Х, 0<q<1

Свойство:

-Любое сжимающее отображение непрерывно.

Доказательство.

Для этого выберем аХ и, полагая у=а, получаем соотношение _у(Fx ,Fа) α(x₁,х₂).

Пусть хU(а,), т.е. (x,а)<, тогда из соотношения (1) получаем (Fx ,Fa) α=.

Из соотношения α=  >0

Таким образом, >0  : (x,a)<  (Fx ,Fa)<

А это значит, что отображение F непрерывно в точке а. Т.к. точка а была выбрана произвольно из Х, то отображение F непрерывно на всем пространстве.

Таким образом, любое сжимающее отображение непрерывно