19. Статистические средние характеристики случайных процессов.

Опр. Средним значением случайного процесса ξ(t) m_ξ(t) наз-ся математическое ожидание случайного процесса в момент времени t:

Оно определяется одномерной функцией распределения F(x,t).

Опр. Дисперсией случайного процесса ξ(t) наз-ся дисперсия сечения случайного процесса, которая так же определяется одномерным распределением:

Опр. Корреляционной функцией случайного процесса ξ(t) наз-ся математическое ожидание произведения двух сечений случайного процесса в моменты времени t₁, t₂:

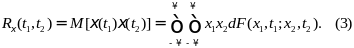
Опр. Ковариационная функция случайного процесса ξ(t) – это математическое ожидание произведения центрированных сечений процесса в моменты времени t₁, t₂:

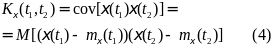
Величину

Называют нормированной ковариационной функцией, или коэффициентом корреляции случайного процесса. При t₁=t₂=t ковариационная функция совпадает с дисперсией случайного процесса:

Для двух случайных процессов ξ(t) и η(t) вводится понятие взаимной функции корреляции, или кросс-корреляции:

а совместная ковариационная функция двух случайных процессов определяется как матричная функция

Свойства корреляционной функции:

1. Корреляционная функция является симметричной функцией своих аргументов R_ξ(t₁,t₂)= R_ξ(t₂,t₁).

2. .

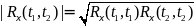Док-во. Следует из нер-ва Коши-Буняковского для мат. ожиданий M²(uv)≤Mu²Mv². Обозначив в нем u= ξ(t₁),

v= ξ(t₂), имеем M²[ξ(t₁) ξ(t₂)]= Mξ²(t₁) Mξ²(t₂).

3. Корреляционная функция случайного процесса является положительно определенной, т.е. n и действительных λ₁, λ₂,…, λ_n: .

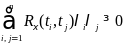4.Пусть 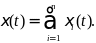Тогда

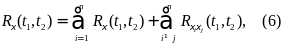
20. Сходимость в среднем квадратичном для случайных процессов.

Процесс удовлетворяющий условию M|ξ(t)|²<+∞ называются процессами с конечными моментами второго порядка, или гильбертовыми процессами.

Опр. Посл-сть ξ_h(t) сходится к ξ(t) по вероятности при h→h₀, если 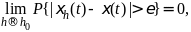т.е. .

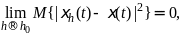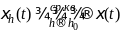Опр. Последовательность ξ_h(t) сходится к ξ(t) в среднем квадратичном при h→h₀, если т.е. или

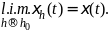
Лемма. Если и 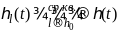, то

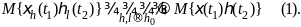
Док-во. Рассмотрим математическое ожидание разности Воспользуемся неравенством Коши-Буняковского

Т.к. рассматриваются процессы с ограниченными моментами второго порядка, то Mξ²(t)<+∞, Mη²(t)<+∞. По условию леммы и определению сходимости в среднем квадратичном, остальные сомножители в правой части стремятся к нулю при h,l→h₀. поэтому

Т. Для того чтобы , необходимо и достаточно, чтобы существовал предел

Док-во. Необходимость. Пусть . В качестве η_l(t) возьмем ξ_l(t), тогда 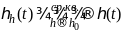. Тогда, по доказанной лемме

Достаточность. Пусть существует конечный предел Тогда

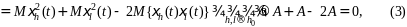
то есть посл-сть сходится ξ_h(t). По лемме Больцано-Вейерштрасса из нее можно выделить подпосл-ть, сходящуюся к ξ(t):

Используя нер-во (a+b)²≤2a²+2b² покажем, что послед-сть ξ_h(t) сходится к этому же пределу ξ(t). Имеем

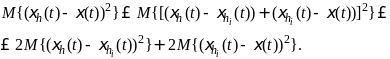
Тогда с учетом (3) и (4) получаем, что

Следствие. Для того чтобы где η-СВ с конечным вторым моментом, необходимо и достаточно, чтобы

21. Непрерывность случайных процессов.

Опр. Случайный процесс ξ(t) называется стохастически непрерывным в точке t₀, если

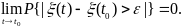
Стохастическая непрерывность процесса относится к свойствам, однозначно определяемым ее двумерным распределением.

Опр. Случайный процесс ξ(t) называется непрерывным в среднем квадратичном в точке t₀, если

Из непрерывности в среднем квадратичном в точке t следует стохастическая непрерывность ξ(t) в той же точке. Это следует из неравенства Чебышева:

Т.1(критерий непрерывности в среднем квадратичном). Для того чтобы процесс ξ(t) был непрерывен в среднем квадратичном в точке t₀, необходимо и достаточно, чтобы его корреляционная функция R(t₁, t₂) была непрерывной в точке t₀=t₁=t₂.

Док-во. Необходимость. Пусть случайный процесс ξ(t) непрерывен в среднем квадратичном в точке t₀, т.е.

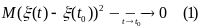
Рассмотрим модуль разности, применяя для него неравенство Коши-Буняковского,

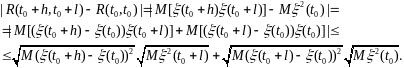
Поскольку корреляционная функция R(t₁, t₂) непрерывна в точке t₀=t₁=t₂, то обе последние разности стремятся к нулю при t→t₀, а это и означает, что соотношение (1) выполняется.

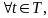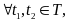Т. 2. Если R(t₁, t₂) непрерывна то R(t₁, t₂) непрерывна, т.е. из непрерывности корреляционной функции при совпадающих аргументах следует ее непрерывность.

Док-во. Так как R(t₁, t₁) и R(t₂, t₂) непрерывны, то из Т.1 следует, что

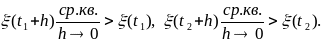
Тогда имеем