42. Оптимальные стратегии в марковских цепях

Рассмотрим цепь Маркова с конечным множеством состояний и матрицей вероятностей переходов . Пусть при переходе из состояния . в состояние i_k мы получаем некоторое вознаграждение r_jk . Например, пусть , - раз­личные места в городе; переход из в i_k означает перевозку пас­сажиров такси по данному маршруту; тогда - это прибыль, входящая в плату за проезд из ( ) в (i_k). Найдем общее вознаг­раждение, которое следует ожидать после переходов цепи Марко­ва за п шагов.

Предположим, что цепь Маркова находится в состоянии и пусть - суммарное среднее вознаграждение за п шагов, если вначале цепь находилась в состоянии . Тогда средний выигрыш после первого шага. Если после первого шага цепь Маркова находится в состоянии 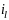, то средний выигрыш на оставшихся п-1 шагах составит . Поэтому полный сред­ний выигрыш за п шагов равен .

Введем матричные обозначения , .

Тогда в матричной форме последнее соотношение может быть пе­реписано как

V(n) = Q + PV(n-1).

В стационарном режиме среднее вознаграждение за один шаг может быть найдено в виде , (10.22) где , финальные вероятности состояний.

43. Система диф.Ур-ий Колмогорова для однородной цепи Маркова с конеч.Числом состояний.

Опред. Пусть (1) . наз. интенсивностью перехода цепи Маркова из состояния в сост. , наз. интенсивностью выхода из состояния , .

Опред. Если , то состояние наз.мгновенным (поглощающим); если , состояние наз. немгновенным.

Опред. Немгновенное состояние наз. регулярным, если и нерегулярным, если . Если все состояние цепи Маркова регулярны, тона наз. регулярной.

Из (1) следует, (2)

Теорема. Для однородной цепи Маркова с конеч.числом состояний переход. вероят-и удовл.системам диф. ур-ий:

(3)

(4)

с начальными условиями (5)

Система (3) наз. системой прямых диф.ур-ий, а (4) – системой обратных диф.ур-ий Колмогорова.

Док-во

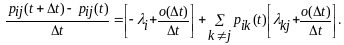Устремив , будем иметь систему (3). Аналогично выводится (4).□

Система прямых диф.ур-ий имеет место и для безусловных вероят-ей сост. : (6)

при любом нач. распределении .

Предположим, что стационарное распределение цепи Маркова , где .При производные , и тогда из системы (6) имеем: . Полученные ур-ия наз. ур-иями равновесия.

Опред. Состояние стохастически непрерывной однородной цепи Маркова с непрерыв. временем наз. достижимым из состояния , если либо , либо , либо .

Опред. Цепь Маркова с непрер.временем наз. эргодической, если .

Для цепи с конеч.числом состояний Х={1,2,….,N} финальные вероятности состояний , всегда .

Ур-ия для вычисления финал.вероят-ей можно получить, переходя к пределу при t→∞ в системе ур-ий (7). Тогда с учетом того, что , имеем

(7)

эта система однозначно определяет финальные вероятности состояний.

44. Процесс гибели и размножения

Будем предполагать, что все состояния процесса регулярны. Для сокращения записей обозначим λ_nn+1=λ_n, λ_nn-1=μ_n. Тогда получаем:

p_nn+1(∆t)= λ_n ∆t+o(∆t),

p_nn-1(∆t)= μ_n ∆t+o(∆t),

p_nn(∆t)= 1-(λ_n + μ_n )∆t+o(∆t).

Можно сказать, что λ_n∆t с точностью до o(∆t) есть вероятность рождения новой особи в популяции из n особей за время ∆t, а μ_n∆t с точностью до o(∆t) - вероятность гибели особи в этой популяции за время ∆t.

Системы прямых и обратных диф. ур-ий Колмогорова для вероятностей переходов процесса имеют вид:

(1)

где μ₀= λ_-1=0, а система ур-ий для безусловных вероятностей состояний:

(2)

Ее можно записать в матричной форме , при этом инфинитезимальная матрица процесса равна

Оказывается, если выполняется условие (3), то процесс гибели и размножения эргодичен, сущ вероятности

, совокупность кот.образует единств. стацион. распределение, совпадающее с эргодическим, т.е. стационарные вероятности состояний равны финальным вероятностям состояний. Для выполнения нер-ва (3) достат., чтобы N, для кот 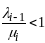при всех . Найдем стацион. вероятности состояний. Система ур-ий равновесия для них, как сл. из (2), имеет вид

(4)

Обознач. 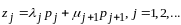.Тогда из (4) получаем

откуда следует, что , для всех j = 0,1,2,…. Следовательно (4)

Вероятность найдем, используя усл. нормировки

Подставляя (4) в это усл., находим

Если то и стационар.(финал.) распределения не существует. Это означает, что эволюция процесса протекает в одну сторону, при этом номер состояния не возрастает.