2. Аксематическое определение вероятности. Свойства вероятности.

Рассматривали случай, когда мера множества элементарных событий была ограниченной и все элементарные события были равновозможные. В данном случае рассматривается определение вероятности свободное от этих ограничений, в основе которого лежит трактовка вероятности как неотрицательной, нормированной, счётно-аддитивной функции множеств, которые являются событиями. Таким образом, определим р(А), . Совокупность подмножеств пространства , на котором может быть определена вероятностная функция, должна быть построена специальным образом. События, которые имеют вероятность, образуют -алгебру или Борелевское множество, т.е. такую совокупность 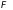, которая является подмножеством множества и удовлетворяет следующим свойствам:

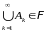3) если случайное событие , то и .

Сформулируем аксематическое определение вероятности: вероятностью р, которая определяется на -алгебре событий , называется числовая функция р(А), где , которая удовлетворяет след. аксиомам:

1)

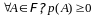
2)

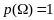
3) если , то .

Из определения следует, что

а) ;

б) вероятность является нормированной мерой, т.е. для неё выполняются условия нормировки.

Совокупность называется аксематическое вероятностным пространством.

Свойства вероятности.

1)

Доказательство. Действительно,

2)

Доказательство.

3)

4)

Д оказательство.

5)

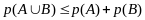
6) пусть , тогда

.

3. Формула полной вероятности. Формула Байеса.

Определение. Говорят, что события образуют полную группу событий, если имеют места следующие соотношения:

1) 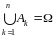2) 3)

Утверждение. Если события 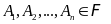образуют полную группу событий, то имеет место следующая формула , где 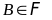. Данная формула называется формулой полной вероятности.

Доказательство. Т.к. события образуют полную группу, то

.

Рассмотрим . Т.к. из определения условной вероятности имеет место, что

.

Из второго и третьего равенства получим:

.

Т.о. окончательно имеем . Данная формула называется формулой Байеса.

Пример.

Для контроля из трёх партий деталей взята для испытания 1 деталь. Какова вероятность обнаружения бракованной продукции, если в первой партии 2/3 деталей бракованные, а во второй и в третьей все детали доброкачественные.

.

4. Схема независимых испытаний Бернулли. Предельная теорема Пуассона.

Два случайных события А и В называются независимыми, если . Если события А и В независимы, то .

Случайные события называются независимыми в совокупности, если : имеет место следующее соответствие

.

Определение. Если , то события называются независимыми парами.

Из независимости в совокупности следует попарная независимость, а из попарной независимости независимость совокупности следует не всегда.

Схема независимых испытаний Бернулли.

Определение. Испытанием называется последовательность из двух актов:

1. создание комплекса условий;

2. наблюдение появившегося события.

Испытания будут независимыми, если наблюдаемые события являются независимыми.

Определение. Независимые испытаниями Бернулли называются такие независимые испытания, для которых вероятность появления события в каждом испытании одинакова и не меняется от испытания к испытанию.

В случае, когда число испытаний не велико на практике пользуются формулой Бернулли:

.

Помимо всего прочего имеет место следующее равенство: . Данное равенство называется условием нормировки.

Если же число испытаний велико, то используют следствия из предельных теорем.

Первая предельная теорема носит название предельная теорема Пуассона. Справедливо следующее предельное соотношение:

.

На практике данная теорема используется, когда .

Доказательство.

По формуле Бернулли:

.

, что и требовалось доказать.

Следствие. Из теоремы Пуассона вытекает, что при большом n справедлива следующая приближенная формула: , где .