1.5. Уравнения движения гироскопа в кардановом подвесе

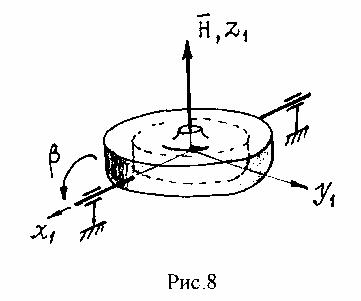
Приведенные выше результаты необходимо уточнить, для чего, в частности, необхо- димо учесть наличие подвеса гироскопа. Очевидно, что без подвеса практическое ис- пользоёвание гироскопа невозможно, а подвес участвует в движении гироскопа. В качест- ве подвеса на практике используют двух-, трехстепенной и трехстепенной с дополнитель- ной рамкой кардановы подвесы в зависимости от назначения прибора, которым определя- ется требуемое число степеней свободы гироскопа. Одна из степеней свободы, связанная с собственным вращением, реализуется конструктивно в гиромоторе (рис.2), размещаемом обычно в кожухе, играющем роль внутренней рамки подвеса. Двухстепенной подвес (рис.8) обеспечивает возможность разворота оси гироскопа относительно лишь одного из направлений, перпендикулярных его оси собственного вращения - по углу . Такие гиро- скопы называют двухстепенными.

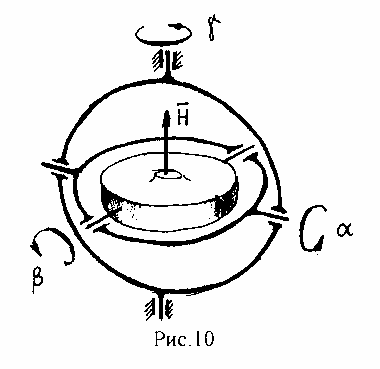
Трехстепенной подвес (рис.9) обеспечивает возможность разворота оси гироскопа относительно двух направлений - по углам и (трехстепенной гироскоп). Однако, ес- ли в этой схеме гироскоп развернется на угол , равный 90^o (или кратный ему), то ось собственного вращения гироскопа совместится с наружной осью подвеса и при этом ги- роскоп потеряет возможность вращаться вокруг вертикальной оси (эффект "сложения рамок подвеса"). Поэтому, если гироскоп предназначен для использования в условиях его возможного произвольного разворота, он оснащается трехстепенным подвесом с допол- нительной рамкой. Рис.10 иллюстрирует один из возможных вариантов подобного подве- са.

Рассмотрим теперь вопрос о том, как изменятся уравнения движения гироскопа (8) с

учетом наличия карданова подвеса. Для конкрет- ности будем полагать, что гироскоп оснащен трехстепенным подвесом, изображенным на рис.9 (отсчет углов на этом рисунке согласован с рис.1). При этом учтем также тот факт, что моменты мо- гут быть приложены к гироскопу только путем создания моментов по осям подвеса и . При этом связь между моментами М и М , прило- женными по осям подвеса, и моментами М_x1 и М_y1, создаваемыми при этом по резалевым осям x₁ и y₁, имеет вид

^M x1

M _b , M _y1

^M _a ^{/ cos b} .

Для получения искомых уравнений следует повторить выполненные ранее выкладки, дополнительно учтя вектор кинетического момента элементов карданова подвеса. В ре- зультате будем иметь следующие уравнения, аналогичные (8):

J_a (b )a^&&

^2J_ab^{a&b& sin b cos b}

_{H b}^& _{cos b}

M _a ,

₍₂₉₎

_Здесь

^J _b ^b&&

^J_ab^{a& 2 sin b cos b}

H a^& cos b

^M b.

^J_a ^{(b) (J} _э ^J _ку ^{) cos2 b}

^J _kz ^{sin 2 b}

^J _py ^,

^Jab

^J _b

^J э ^J ky ^J kz ^,

^J _э ^J _kx ^,

J_э - экваториальный момент инерции гироскопа, J_kx, J_ky, J_kz - моменты инерции кожуха гироскопа относительно резалевых осей x₁, y₁, z₁ соответственно (см. рис.8), J_py - момент инерции рамки (Р на рис.9) относительно оси вращения по углу .

Естественно, если инерционностью элементов подвеса пренебречь, то уравнения (29)

переходят в уравнения (8).

Входящие в уравнения (29) М и М в общем случае включают в себя "полезную" со- ставляющую - управляющие моменты или моменты, зависящие от измеряемых парамет- ров - и "вредную" составляющую, каковой являются моменты сухого и вязкого трения в осях подвеса, моменты, обусловливаемые деформацией жгутов, с помощью которых по- дается питание на гиромотор, и т.п.

_динат