1. Основные сведения из теории гироскопа

1.1. Движение абсолютно твердого тела вокруг неподвижной точки

Для описания движения тела вокруг неподвижной точки О введем две ортогональные правые системы координат: систему координат Оxyz, связанную с телом и ориентирован- ную относительно него пока произвольным образом, и неподвижную, инерциальную сис- тему координат O . Тогда ориентация тела в инерциальном пространстве будет опреде- ляться взаимной ориентацией введенных систем координат. Она же характеризуется тремя эйлеровыми углами , и , вводимыми, например, так, как показано на рис.1. На этом

_{рисунке изображены также векторные составляющие a}^& _{, b}^& _{, j}^&

_{угловой скорости разво-}

рота тела ^w на упомянутые углы. Из астрономии в гироскопию перешли названия вра- щательных движений по углам , , : соответственно прецессия, нутация и ротация (или собственное вращение). Однако, правильнее связывать указанные составляющие вращательного движения тела с причинами, их вызывающими, о чем будет сказано ниже.

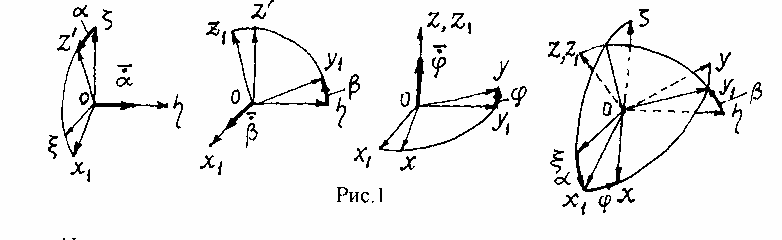
_{Используя рис.1 и обозначая индексом "о" орт соответствующий оси можно записать}

связь векторов

a^& , b^& , j^&

с их величинами

_o

a^& ,b^& ,j^&

_o

^{a& a& cos by}₁

1

b^& b^&x ^o ,

^{a& sin bz}₁ ^,

₍₁₎

1

j^& j^&z ^o .

_{Сумма векторов}

a^& , b^&

и j^&

_{есть, очевидно, угловая скорость тела w , т.е.}

_{w a}^&

_b^& _j^& _.

Проектируя обе части этого равенства на оси связанной системы координат, исполь-

_{зуя при этом принятые в теоретической механике обозначения для проекций вектора w}

p

с учетом (1) получим

w x ^o, q

w y ^o, r

^{w z o} ,

p a^& cos b sin j

q a^& cos b cosj

b^& cosj ,

b^& sin j ,

₍₂₎

_{r a}^& _{sin b}

_j^&_.

Это - кинематические уравнения Эйлера для вращательного движения тела вокруг неподвижной точки. Они связывают составляющие угловой скорости тела ^w с углами, характеризующими ориентацию тела.

Уравнения, связывающие составляющие угловой скорости с действующими на тело

моментами называются динамическими уравнениями. Впервые они были получены так- же Эйлером. Выводятся эти уравнения на базе фундаментальной теоремы теоретической механики об изменении момента количества движения (кинетического момента) ^G тела.

Согласно этой теореме

_G^& _{M , (3)}

где ^M - суммарный момент, действующий на тело. Если теперь, воспользовавшись про- извольностью выбора ориентации связанной системы координат, направить оси x, y, z по главным осям инерции тела, то выражение для ^G будет иметь достаточно простой вид

^{G pJ} _x ^{x o qJ} _y ^{yo rJ} _z ^{z o,} (4)

где J_x, J_y, J_z - моменты инерции тела относительно осей x, y и z соответственно. Под- ставляя (4) в (3) и проектируя обе части векторного уравнения на оси связанной системы координат, получим требуемые динамические уравнения

J _x p^&

J _yq^&

^J _z ^r&

J _z J _y qr M _x ,

J _x J _z rp M _y,

^J _y ^J _x ^{pq M} _z ^.

(5)

Полную систему уравнений вращательного движения твердого тела вокруг неподвиж- ной точки составляют кинематические уравнения (2), динамические уравнения (5) и соот- ношения для определения составляющих момента, имеющие в общем случае вид

^M _x ^M _x ^{t;a, b,j ,}

M _y M _y t;a, b,j ,

^M _z ^M _z ^{t;a, b,j .}

(6)

Для получения решения этой системы, описывающего вращение тела, необходимо за- дать начальные условия: значения на начальный момент времени углов , , и состав- ляющих угловой скорости p, q, r.

Даже при условии, что на тело действует момент, обусловленный только силой тяже-

сти, приведенная система уравнений допускает получение решения в элементарных функ- циях лишь в отдельных случаях (случаи Эйлера-Пуансо, Лагранжа-Пуассона и Ковалев- ской).