2.3.5. Исследование динамики системы управления модального регулятора со статическим наблюдателем для объектов первого порядка с запаздыванием

В этом разделе будем исследовать динамики системы управления, в которой используется только что синтезированный модальный регулятор со статическим наблюдателем.

Для этого используем написанную в языке С++ комплексную программу (исходный код файла MR_MO1.cpp).

Для начала рассмотрим случай, когда объект управления описывается динамической моделью первого порядка с запаздыванием, то есть имеет одинаковый порядок что и модель. На рис. 2.9. показан график отработки задания и возмущения в системе управления модального регулятора со статическим наблюдателем. Для убеждения в том, что регулятор точно работает, сначала возьмем объект, который идентичен по параметрам по сравнению с моделью. Как видно на графике, регулятор точно отработает задание и возмущение без статической ошибки.

Рис. 2.9.График отработки задания и возмущения в системе управления модального регулятора со статическим наблюдателем.

Далее рассмотрим работу регулятор в случае разных параметрах объекта и модели. На рис. 2.10 показан график отработки задания и возмущения регулятором в случае отличия по всем трем параметрам: коэффициент усиления, постоянная времени и запаздывания в объекте и модели. В этом случае наблюдается статическая ошибка выходного значения, что объясняется наличием статический наблюдатель в структуре регулятор.

Величина статической ошибки, как будет показано в главе 5 почти пропорционально зависит от отношения запаздывание к постоянной времени, и конечно от неточность в параметрах модели.

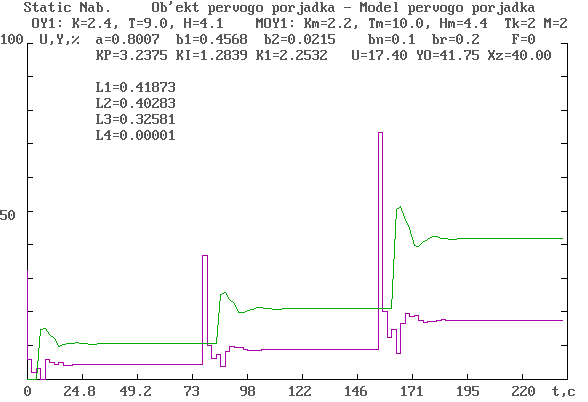
Рис. 2.10.График отработки задания и возмущения в системе управления в случае неточности параметров модели.

Теперь рассмотрим работу регулятор в случае объекта третьего порядка, а модель – первого порядка. Динамики системы управления модального регулятора со статическим наблюдателем для объекта третьего порядка показаны на рис. 2.11 и рис. 2.12.

Рис. 2.11.График отработки задания и возмущения в системе управления для объекта третьего порядка.

Рис. 2.12.График отработки задания и возмущения в системе управления для объекта третьего порядка.

Смотря на эти графики можно сказать, что в обоих случаях присутствуют статическая ошибки, при чем в случае рис. 2.11 ошибка меньше чем в рис. 2.12, что объясняется степенью точности модели.

Так же можно сказать, что для объекта первого динамики системы имеет лучшие характеристики по сравнению с объектом третьего порядка.

2.4. Синтез модального регулятора с астатическим наблюдателем для объектов первого порядка с запаздыванием

2.4.1. Синтез астатического наблюдателя для объектов первого порядка с запаздыванием в случае кратного отношения запаздывания к периоду квантования

Введение в схему наблюдателя цифрового интегратора позволяет получить на его выходе оценку возмущения, действующего на объект управления и обеспечить отработку сигнала задания с нулевой статической ошибкой даже при использовании приближенной модели объекта. Для расчета коэффициентов наблюдателя в соответствии со структурной схемой Рис.2.9. запишем систему разностных уравнений, описывающих динамику контура наблюдения (М=1)

(2.26)

Характеристическое уравнение этой системы получим на основе определителя:

(2.27)

Рис. 2.13. Структурная схема системы управления (для М=1)

Приравнивая коэффициенты при одинаковых степенях z этих уравнений и решая систему уравнений, получим

(2.28)

Аналогично, для произвольного запаздывания M (рис. 2.14) получим следующие рекуррентные формулы для вычислений коэффициентов астатического наблюдателя:

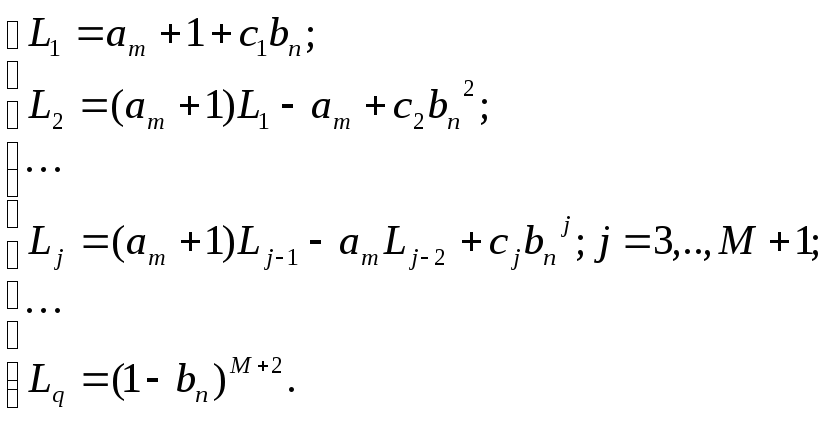(2.29)

где ,- число сочетаний из М+2 по j, j=2..M.

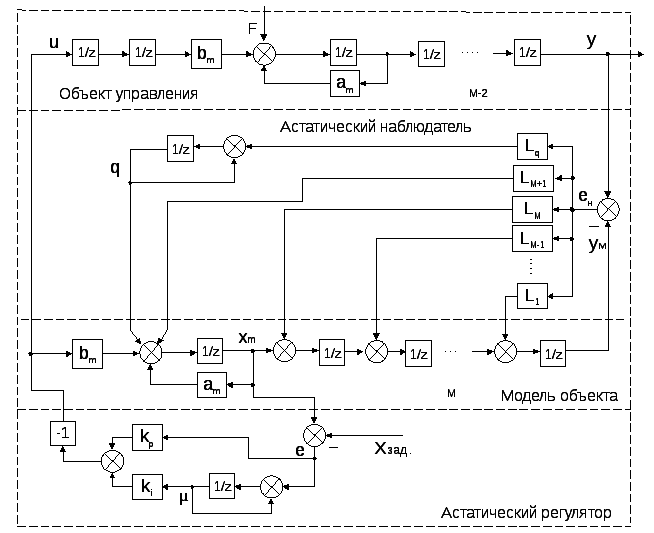
Рис. 2.14. Структурная схемасистемыуправления для произвольного запаздывания М