2.2. Цифровая модель объекта первого порядка с запаздыванием

Вначале рассмотрим типовые модели 1-ого порядка для объектов с запаздыванием в управлении h_y и (или) измерении h_и. На практике трудно выделить эти составляющие запаздывания, к тому же на динамику одномерной системы влияет только суммарное запаздывание h в объекте относительно его входа и выхода. В связи с этим передаточная функция объекта управления может быть записана в виде:

, (2.1)

где K, T, h – коэффициент усиления, постоянная времени и суммарное запаздывания объекта по каналам управления и измерения. Коэффициент усиления может использоваться как в размерной, так и безразмерной форме (%/%). При использовании размерной формы входные и выходные сигналы, вводимые в регулятор должны масштабироваться таким образом, чтобы внутренние сигналы в цифровом регуляторе менялись от 0 до 100 %.

Перейдем к дискретному описанию динамики модели объекта управления, для чего зададимся величиной периода квантования (опроса) , с которым будет работать данный регулятор. Рекомендуется выбирать значениеблизкое к величине Т95/15 [3], хотя это не жесткое требование. Для получения максимально простой структуры регулятора и простых расчетных формул выберем вначале такое значение, чтобы оно было кратно величине запаздывания, т.е.– целое число, гдеэто количество элементарных блоков задержки сигнала на один период квантования в звене запаздывания. Тогда, перейдя к дискретному времени, получим дифференциально-разностное уравнение модели объекта с запаздыванием[3]:

, (2.2)

где - номер периода квантования.

Если выбранный период квантования не кратен величине запаздывания, то, применяя модифицированный Z-преобразование, и используя результат, полученный в [4], имеем следующее описание объекта:

(2.3)

где ;

с  дробная часть отношения .

2.3. Синтез модального регулятора со статическим наблюдателем для объектов первого порядка с запаздыванием

Рассмотрим дискретные описания объектов с запаздыванием и подробнее структуры линейных регуляторов с использованием статического наблюдателя полного порядка и дадим их методики расчета.

2.3.1. Синтез статического наблюдателя для объектов первого порядка с запаздыванием в случае кратного отношения запаздывания к периоду квантования

Рассмотрим вначале более простой случай расчета, когда имеется объект первого порядка, а период квантования кратен величине запаздывания при задержке сигналов в объекте управления на M=1. Соответствующая структурная схема системы приведена на Рис. 2.2.

Идея ее построения [1,7], как описано выше, основана на переносе запаздывания на выход модели объекта, что позволяет получить оценку упрежденного значения выходного сигнала объекта. Соответствие движений в модели и объекте достигается за счет использования статического наблюдателя полного порядка.

Для облегчения расчетов предлагается применить принцип раздельного синтеза контуров регулирования и наблюдения [8,17], а также теорию модального цифрового управления [16]. Использование в методике расчета параметров наблюдателя основ теории модального управления позволяет получить простые расчетные формулы. Это объясняется тем, что вместо решения системы нелинейных алгебраических уравнений (уравнение типа Риккати) необходимо решать линейную систему алгебраических уравнений.

Для расчета коэффициентов наблюдателя в соответствии со структурной схемой Рис. 2.3. запишем систему разностных уравнений, описывающих динамику только контура наблюдения «Модель объекта – Статический наблюдатель»

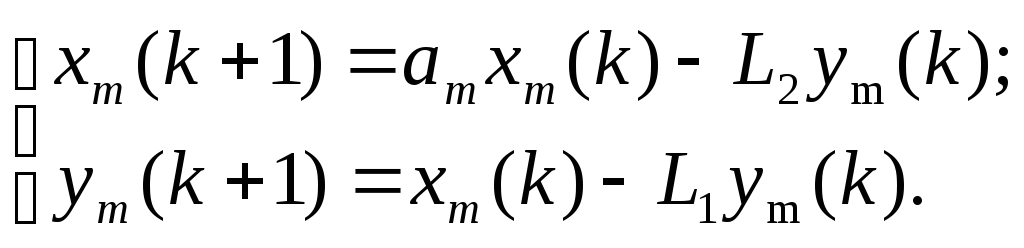(2.4)

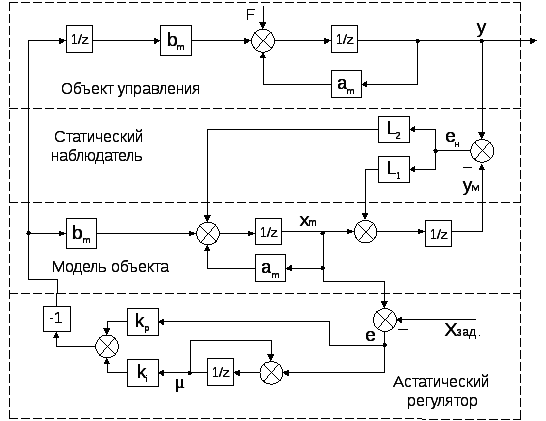
Рис. 2.2.Структурная схема системы управления объектом первого порядка с запаздыванием и модальным регулятором с наблюдателем (для М=1)

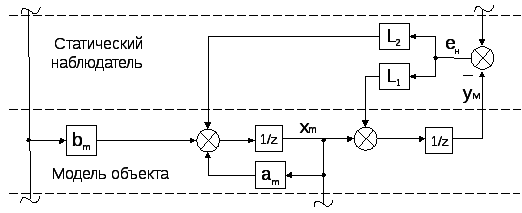
Рис. 2.3.Контура наблюдения для синтеза статического наблюдения

Характеристическое уравнение этой системы получим на основе определителя

=0 (2.5)

Согласно теории модального управления, необходимо, чтобы все корни характеристического уравнения замкнутой системы располагались нужным образом и внутри единичной окружности комплексной плоскости Z. Для простоты настройки наблюдателя потребуем, чтобы все корни были одинаковыми (кратными) и располагались на действительной полуоси, в интервале от 0 до 1. Такой подход позволяет настройщику варьировать лишь одну величинув диапазоне от 0 до 1, где- корень наблюдателя кратности 3. Как показали исследования, этот подход позволяет подобрать такое значение корня, которое обеспечивает хорошую динамику наблюдателя. Так как наблюдатель работает на точную модель объекта, то допустимо устанавливать даже значение.

Характеристическое уравнение замкнутого контура «наблюдатель – модель» будет иметь вид[16] :

=0 (2.6)

где - комплексная переменная,- единичная матрица размером 2х2.

Уравнение (2.6) является базовым уравнение, на котором базируется вся методика расчета параметров наблюдателей и регуляторов.

Раскрывая выражения (2.6) и приравнивая коэффициенты полинома при одинаковых степенях , получим следующую систему линейных алгебраических уравнений.

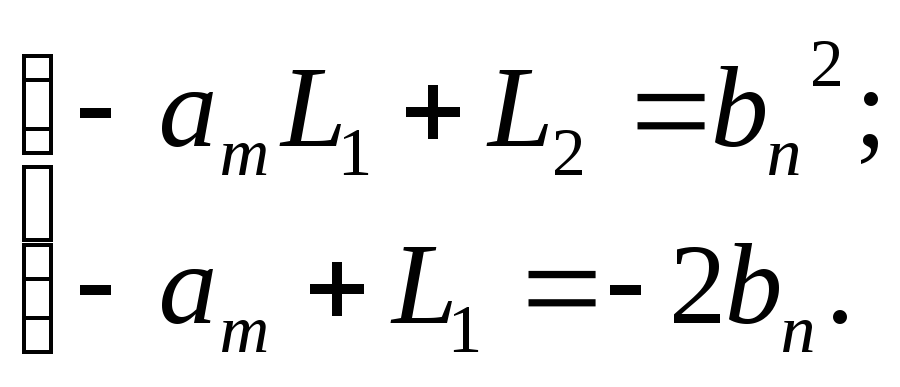(2.7)

Из этой системы получаем формулы для расчета коэффициентов статического наблюдателя полного порядка

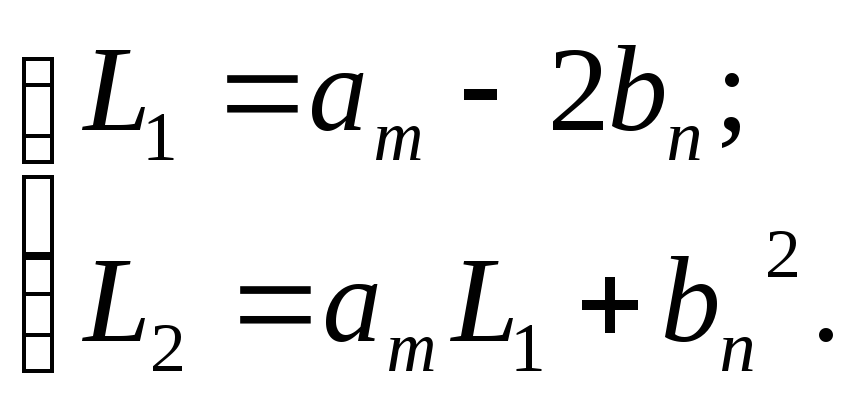(2.8)

Аналогично выведем формулы вычисления коэффициентов наблюдателя для величины запаздывания М=2. Для расчета коэффициентов наблюдателя в соответствии со структурной схемой (рис. 2.4.) запишем систему разностных уравнений, описывающих динамику только контура наблюдения:

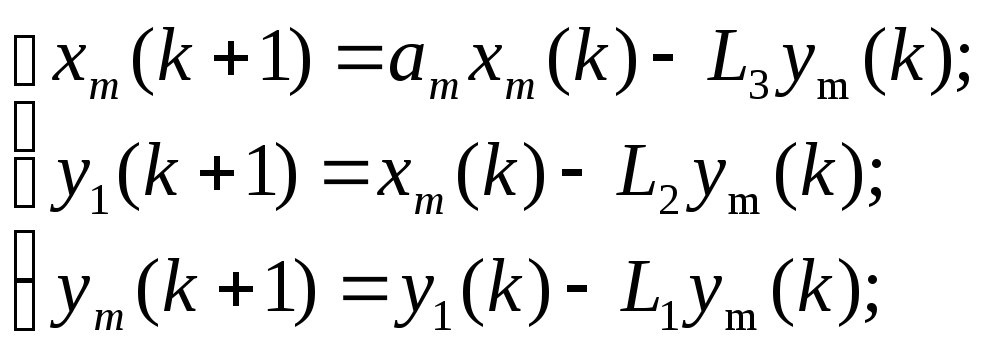(2.9)

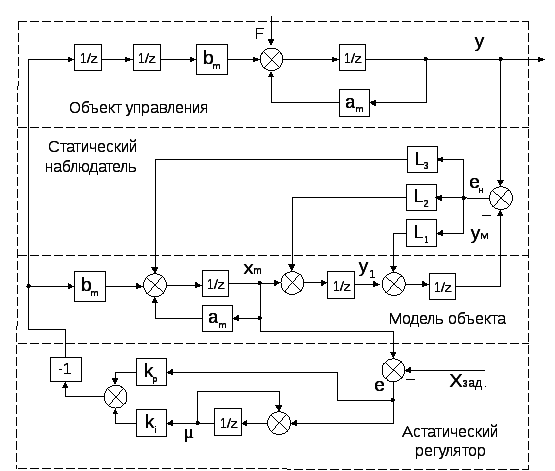
Рис. 2.4.Структурная схемасистемыуправления объектом первогопорядка сзапаздываниемирегуляторомс наблюдателем (для М=2).

Опуская промежуточные выкладки, получим следующие формулы для статического наблюдателя при запаздывании на М=2

(2.10)

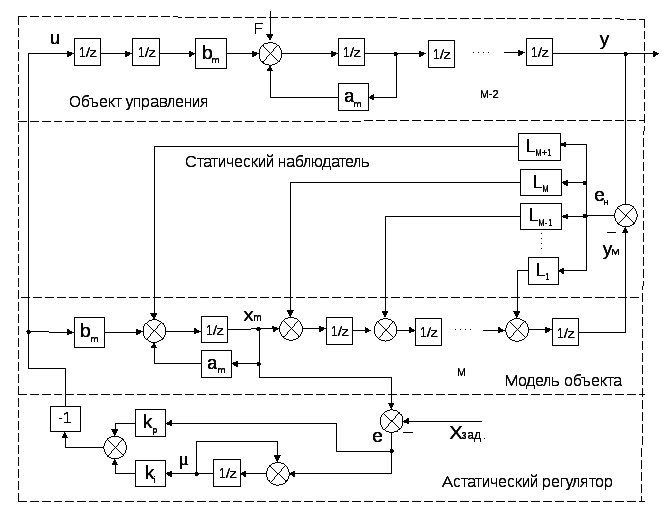
Рис. 2.5.Структурная схемасистемыуправления для произвольного запаздывания М.

Аналогично, для произвольного запаздывания M получим следующие рекуррентные формулы для вычислений коэффициентов статического наблюдателя полного порядка, схема которого приведена на рис. 2.5.

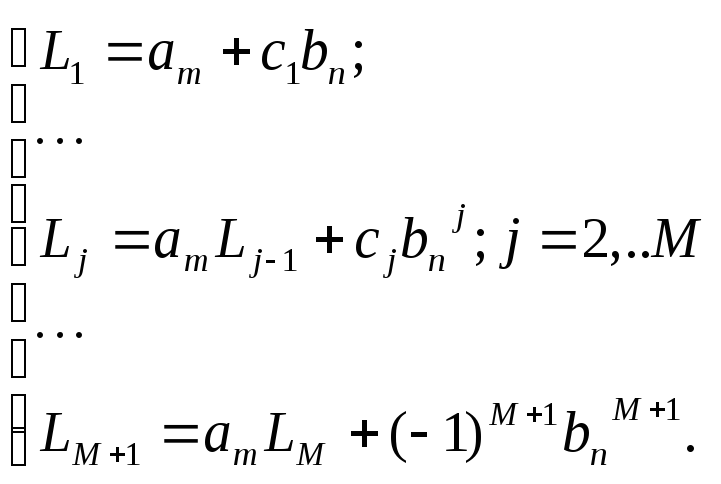(2.11)

где ,- число сочетаний из М+1 по j; j=2..M.