Глава 1. Обзор литературы и постановка задачи

1.1. Технологические объекты с запаздыванием

Характерной особенностью большинства технологических объектов является наличие значительных запаздываний в каналах управления и измерения, что объясняется конечной скоростью распространения сигналов и информации в объектах (транспортное запаздывание).

Другой особенностью большинства объектов управления является их многоемкостность (наличие каскадов или цепочек технологических объектов). Многоемкостность приводит к повышению порядка дифференциального уравнения объекта, т.е. к появлению множества достаточно малых постоянных времени объекта. В этом случае, с целью упрощения динамической модели объекта, вводится дополнительное звено запаздывания, величина которого примерно равна сумме отбрасываемых постоянных времени объекта. Такое запаздывание называется динамическим.

Кроме этого в некоторых объектах, охваченных контуром обратной связи (объекты с рециклом) появляется дополнительное запаздывание в контуре рециркуляции. Описания систем, содержащих разные типы запаздывания, очень подробно приведены в работах [1].

Наличие запаздывания в технологических объектах резко ухудшает динамику замкнутой системы. Обычно при отношении /Т>0,5 типовые законы управления не могут обеспечить высокую точность и быстродействие процесса регулирования [2]. Главной причиной здесь является резкое снижение критического коэффициента усиления системы при увеличении запаздывания в объекте управления.

1.2. Определение класса рассматриваемых объектов управления

Первоочередной задачей при разработке и исследовании алгоритмов управления является отнесение исследуемого объекта к определенному классу, так как от этого во многом зависит выбор того или иного метода синтеза оптимального управления. При этом необходимо учитывать такие особенности объекта, как наличие или отсутствие запаздывания, линейность и нелинейность характеристик, стационарность или нестационарность параметров объекта, его структура, наблюдаемость координат объекта и возмущений, уровень и характер случайных помех, и ряд других факторов.

Рассматривая особенности объектов управления, следует отметить, что принципиально все объекты нестационарны. Однако опыт эксплуатации регуляторов с фиксированными настройками показывает, что для значительного класса объектов нестационарность параметров слабо выражена или носит периодический характер с небольшими колебаниями около некоторого среднего уровня, на который настраивается регулятор. Это позволяет рассматривать такие объекты, как квазистационарные и рассчитывать параметры регуляторов для номинальных (средних) значений характеристик объекта управления.

Возмущения, действующие на объект, можно условно разделить на детерминированные и стохастические. В обоих случаях желательно замерять эти возмущения или знать их статистические характеристики, что на практике не всегда возможно. В практике управления одной из основных задач регулятора является отработка внешних возмущений. Импульсные возмущения сводятся фактически к отработке ненулевых начальных условий. В этом случае в системе существует только собственное движение, определяющееся динамическими свойствами объекта структурой и параметрами регулятора. Это весьма важный вид движения позволяющий оценить устойчивость и качество динамических процессов в замкнутой системе управления.

При изменении нагрузки на технологический агрегат действуют возмущения в виде ступенчатых функций времени. Многие непрерывные функции времени произвольного вида также можно аппроксимировать с помощью серии ступенчатых функций времени. В этом случае требуется астатический (изодромный) регулятор, имеющий заданную динамику отработки таких возмущений. Часто амплитуду ступенчатого возмущения замерить не представляется возможным.

Учтем, что большинство объектов имеют высокий порядок со значительным числом ненаблюдаемых координат, но многие их них можно описать дифференциальным уравнением первого, второго или третьего порядка с запаздыванием, которое учитывает малые постоянные времени объекта. Этот прием полностью оправдал себя практикой расчета настроек типовых регуляторов для промышленных объектов по их кривым разгона [2].

Следует отмечать, что описания промышленных объектов как объекты того или иного порядка еще зависит от конкретного случая, от цели и задачи регулирования, от специфических характер регулируемых величин. Например, для регулирования величин, не требующих высокой точности или допускающих достаточного большого зона колебания выходного сигнала, то достаточно описать эти объекта как объект первого или второго порядка, что намного упрощает процесс синтеза и расчета систем управления.

Вначале рассмотрим типовые модели 1-ого порядка для объектов с запаздыванием в управлении h_y и (или) измерении h_и. На практике трудно выделить эти составляющие запаздывания, к тому же на динамику одномерной системы влияет только суммарное запаздывание h в объекте относительно его входа и выхода. В связи с этим передаточная функция объекта управления может быть записана в виде:

, (1.1)

где K, T, h – коэффициент усиления, постоянная времени и суммарное запаздывания объекта по каналам управления и измерения. Коэффициент усиления может использоваться как в размерной, так и безразмерной форме (%/%). При использовании размерной формы входные и выходные сигналы, вводимые в регулятор должны масштабироваться таким образом, чтобы внутренние сигналы в регуляторе менялись от 0 до 100 %.

Учитывая цифровую реализацию регуляторов, перейдем к дискретному описанию динамики модели объекта управления, Для этого зададимся величиной периода квантования (опроса) , с которым будет работать данный регулятор. Рекомендуется выбирать значениеблизкое к величине Т95/15 [3], хотя это не жесткое требование. Для получения максимально простой структуры регулятора и простых расчетных формул выберем вначале такое значение, чтобы оно было кратно величине запаздывания, т.е.– целое число, гдеэто количество элементарных блоков задержки сигнала на один период квантования в звене запаздывания. Тогда, перейдя к дискретному времени, получим дифференциально-разностное уравнение модели объекта с запаздыванием[3]:

, (1.2)

где - номер периода квантования.

Если выбранный период квантования некратен величине запаздывания, то, применяя модифицированный Z-преобразование, и используя результат, полученный в [4], имеем описание объекта в пространство состояния вход-выход:

(1.3)

Динамической моделью промышленного многоемкостного объекта является инерционная модель второго порядка с запаздыванием в управлении и (или) измерении. Передаточная функция такой модели имеет вид:

(1.4)

где K – коэффициент усиления, T₁, Т₂ – постоянные времени, τ– эквивалентная величина запаздывания в объекте по каналу управления и измерения. Коэффициент усиления может использоваться как в размерной, так и безразмерной форме (%/%).

Введем обозначения: Т_К – период квантования, - отношение запаздывания к периоду квантования, причем М – целая часть,с – дробная часть отношения. Величину М будем также называть числом тактов запаздывания или величиной задержки в объекте в периодах квантования.

Если период квантования не кратен величине запаздывания, то, применяя модифицированное Z-преобразование [1] к передаточной функции (1.4), получим описание динамики объекта в координатах вход - выход:

(1.5)

где коэффициенты объекта вычисляются по формулам:

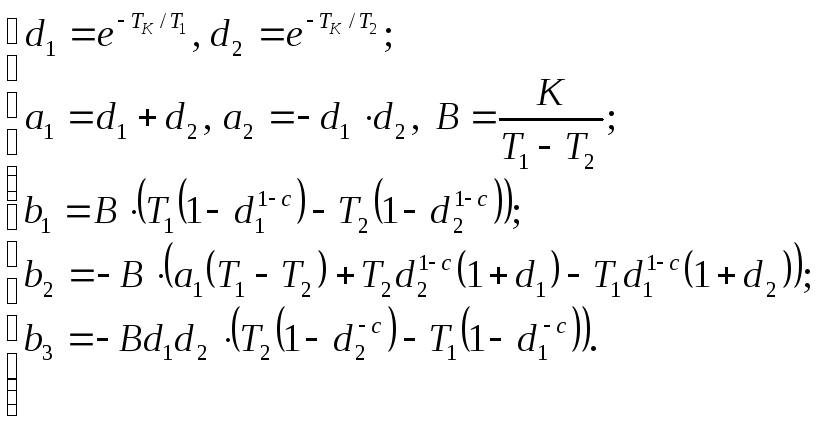(1.6)

Описать динамику объекта второго порядка можно и в пространстве состояний, например, в канонической форме наблюдаемости [8]:

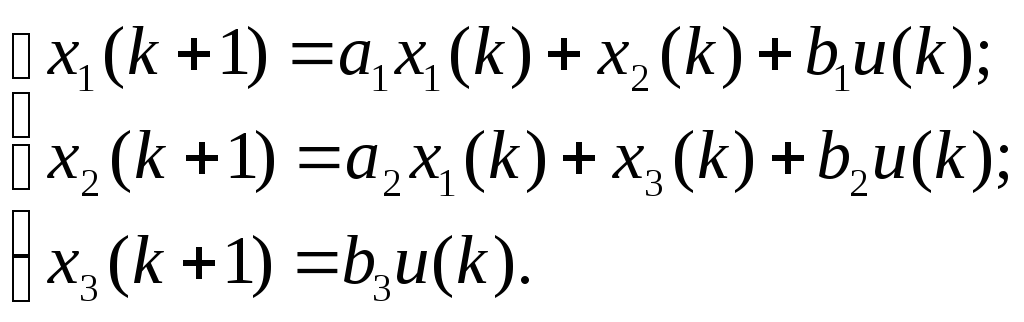(1.7)

Здесь - выход объекта,и- недоступные для измерения внутренние переменные объекта. Удобство этого описания состоит в том, что в нем используются те же коэффициенты, что и в модели объекта. Кроме этого, как показали расчеты, только использование этой модели позволяет получить рекуррентные формулы для вычисления коэффициентов наблюдателя полного порядка.

С помощью модифицированного Z-преобразования получаем дискретное описание для объекта третьего порядка с запаздыванием в координатах вход-выход:

_(1.8)

_где:

_(1.9)

Системы уравнений (1.5) и (1.7) описывает динамику и более сложных объектов управления:

- колебательного звена вида:

(1.10)

- неминимально-фазового звена вида:

. (1.11)

Коэффициенты описания для этих передаточных функций также могут быть получены с помощью модифицированного Z– преобразования.

Отметим, что объект типа (1.8) будет использовать также в качестве базового при исследовании цифровых систем управления на ЭВМ.