
- •I. Анализ системы автоматического управления.
- •1) Передаточная функция по управляющему воздействию в разомкнутом состоянии:
- •2) Передаточная функция в замкнутом состоянии:
- •3) Характеристическое уравнение системы в разомкнутом состоянии.
- •4) Проверка устойчивости линейной сау по критерию Михайлова.
- •5) Проверка устойчивости линейной сау с помощью критерия Найквиста.
- •1.2 Определение ошибки заданной сау в установившимся режиме.
Исходные данные:
С
 хема:
хема:
![]()
![]()
![]()
Рис. 1.1
Заданные параметры:
К=0.9 Т=0.5 τ=0.005
К1=15 Т1=0.025
К2=1.1 Т2=0.08
К3=12 Т3=0.13
К5=2.5 Т4=0.18
Т5=0.19
I. Анализ системы автоматического управления.
1) Передаточная функция по управляющему воздействию в разомкнутом состоянии:
Пусть:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Звенья системы Wо.с(р) и W1(p) соединены обратной связью, поэтому их эквивалент будем считать по формуле:

T01=T*T1=0.5*0.025=0.0125
T02=T+T1+T*K1=0.5+0.025+0.5*0.15=8.025
Т.к все остальные звенья соединены последовательно, то передаточную функцию в разомкнутом состоянии будем искать как произведение этих звеньев:
![]()


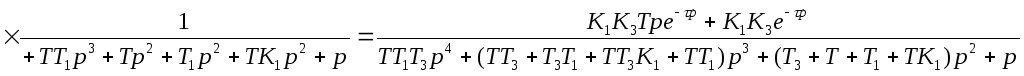
Подставив численные значения, получим:

![]() .
.
2) Передаточная функция в замкнутом состоянии:
![]()
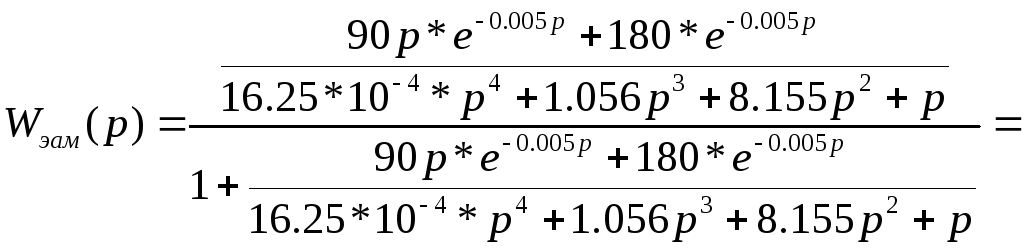
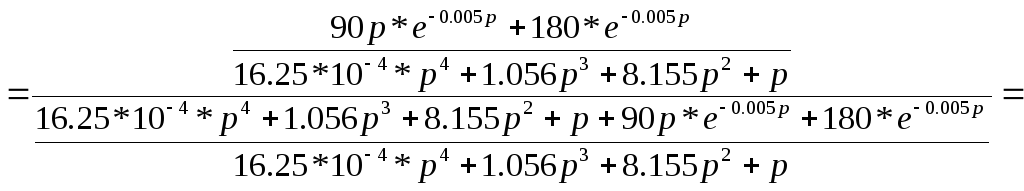
![]() .
.
3) Характеристическое уравнение системы в разомкнутом состоянии.
Для того, чтобы определить характеристическое уравнение системы необходимо приравнять знаменатель передаточной функции в разомкнутом состоянии к нулю.
![]() =0
=0
Характеристическое уравнение системы в замкнутом состоянии.
![]() =0
=0
4) Проверка устойчивости линейной сау по критерию Михайлова.
Критерий Михайлова относиться к частотным критериям, и позволяет оценить устойчивость замкнутой системы по виду годографа, которой находится из характеристического уравнения.
Критерий устойчивости Михайлова: для устойчивости системы необходимо и достаточно , чтобы вектор D(jω), описывающий своим концом кривую Михайлова при изменении частоты ω от -∞ до +∞ , начав свое движение с положительной действительной оси и вращаясь против часовой стрелки, последовательно проходил n квадрантов, нигде не обращаюсь в нуль.
D(p)=
![]() =0
=0
Делаем замену p=jω, получаем
D(jω)=
![]()
![]()
![]()
Выделяем из данного уравнения вещественную и мнимую части:
P(ω)=
![]()
Q(ω)=
![]()
Вычисляем полученные выражения Q(ω) и P(ω) подставляя в них значения частот ω. Полученные результаты занесены в таблицу 1.1.
P(0)=
![]()
Q(0)=
![]()
И так далее.
Таблица 1.1 Критерий Михайлова.
|
ω, с-1 |
0 |
1 |
3 |
5 |
7 |
9 |
11 |
|
P(ω) |
180 |
171.85 |
106.798 |
-22.688 |
-215.315 |
-469.3 |
-782.197 |
|
Q(ω) |
0 |
89.93 |
241.788 |
372.9 |
344.6799 |
49.03 |
-404.7 |
|
|
|
|
|
|
|
Q(ω) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
700 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
500 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
300 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
-600 |
-500 |
-400 |
-300 |
-200 |
-100 |
0 -100 |
100 |
200 |
|
P(ω) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-300 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-500 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.2 Критерий Михайлова.
Из графика видно, что кривая Михайлова проходит через три квадранта (I, II, III), это означает выполнение критерия Михайлова, т.е. система устойчива.












 700
700