
- •Фам Ван Нгуен
- •Глава 3. Синтез модальных регуляторов для объектов второго порядка с запаздыванием 52
- •Глава 4. Разработка оптимальных по быстродействию регуляторов с наблюдателем для объектов с запаздыванием 85
- •Глава 5. Исследование динамики и практическая реализация модальных регуляторов с наблюдающими устройствами 95
- •Введение
- •Глава 1. Обзор литературы и постановка задачи
- •1.1. Технологические объекты с запаздыванием
- •1.2. Определение класса рассматриваемых объектов управления
- •1.3. Обзор методов синтеза регуляторов для объектов управления с запаздыванием
- •1.4. Постановка задачи исследования
- •Глава 2. Синтез модальных регуляторов для объектов первого порядка с запаздыванием
- •2.1. Разработка обобщенной структурной схемы регулятора с наблюдателем для объектов с запаздыванием
- •2.2. Цифровая модель объекта первого порядка с запаздыванием
- •2.3. Синтез модального регулятора со статическим наблюдателем для объектов первого порядка с запаздыванием
- •2.3.1. Синтез статического наблюдателя для объектов первого порядка с запаздыванием в случае кратного отношения запаздывания к периоду квантования
- •2.3.2. Синтеза астатического регулятора состояния для объектов первого порядка с запаздыванием в случае кратного отношения запаздывания к периоду квантования
- •2.3.3. Синтез статического наблюдателя для объектов первого порядка с запаздыванием в случае некратного отношения запаздывания к периоду квантования
- •2.3.4. Синтез астатического модального регулятора состояния для объектов первого порядка с запаздыванием в случае некратного отношения запаздывания к периоду квантования
- •2.3.5. Исследование динамики системы управления модального регулятора со статическим наблюдателем для объектов первого порядка с запаздыванием
- •2.4. Синтез модального регулятора с астатическим наблюдателем для объектов первого порядка с запаздыванием
- •2.4.1. Синтез астатического наблюдателя для объектов первого порядка с запаздыванием в случае кратного отношения запаздывания к периоду квантования
- •2.4.2 Синтез астатического наблюдателя для объектов первого порядка с запаздыванием в случае некратного отношения запаздывания и период квантования
- •2.4.3. Исследование динамики системы управления модального регулятора с астатическим наблюдателем для объектов первого порядка с запаздыванием
- •Глава 3. Синтез модальных регуляторов для объектов второго порядка с запаздыванием
- •3.1. Цифровые модели объектов второго порядка с запаздыванием
- •3.2. Синтез модального регулятора со статическим наблюдателем для объектов второго порядка с запаздыванием
- •3.2.1. Синтез статического наблюдателя для объектов 2-ого порядка с запаздыванием в случае кратного отношения запаздывания и период квантования
- •3.2.2. Синтез астатического регулятора состояния для объектов 2-ого порядка с запаздыванием в случае кратного отношения запаздывания к периоду квантования
- •3.2.3 Синтез статического наблюдателя для объектов 2-ого порядка с запаздыванием в случае некратного отношения запаздывания и период квантования
- •3.2.4. Синтез астатического регулятора состояния для объектов 2-ого порядка с запаздыванием в случае некратного отношения запаздывания и период квантования
- •3.2.5. Исследование динамики системы управления модального регулятора со статическим наблюдателем для объектов второго порядка с запаздыванием
- •3.3. Синтез модального регулятора с астатическим наблюдателем для объектоввторого порядка с запаздыванием.
- •3.3.1 Синтез астатического наблюдателя для объектов 2-ого порядка с запаздыванием в случае кратного отношения запаздывания и период квантования
- •3.3.2 Синтез астатического наблюдателя для объектов 2-ого порядка с запаздыванием в случае некратного отношения запаздывания и период квантования
- •3.3.3. Исследование динамики системы управления модального регулятора с астатическим наблюдателем для объектов второго порядка с запаздыванием
- •Глава 4. Разработка оптимальных по быстродействию регуляторов с наблюдателем для объектов с запаздыванием
- •4.1. Обобщенная структурная схема оптимального по быстродействию регулятора для объекта с запаздыванием
- •4.2. Астатический оптимальный по быстродействию регулятордля объекта первого порядка с запаздыванием
- •4.2.1 Структурная схема оптимального по быстродействию регулятора для объектов первого порядка с запаздыванием.
- •4.2.2. Исследование динамики системы управления модального регулятора со статическим наблюдателем для объектов первого порядка с запаздыванием
- •4.3. Оптимальный по быстродействию регулятор для объектов второго порядка с запаздыванием.
- •4.3.1 Структурная схема оптимального по быстродействию регулятора для объектов второго порядка с запаздыванием.
- •4.3.2. Исследование динамики системы управления модального регулятора со статическим наблюдателем для объектов второго порядка с запаздыванием
- •Глава 5. Исследование динамики и практическая реализация модальных регуляторов с наблюдающими устройствами
- •5.1. Описание комплекса программ, разработанных для исследований динамики систем управления с разработанными регуляторами.
- •5.2. Исследование динамики объекта колебательного вида и неминимально-фазовового объекта.
- •5.2.1. Исследование динамики объекта колебательного вида
- •5.2.2. Исследование динамики неминимально-фазового объекта
- •5.3. Исследование зависимости статической ошибки от отношения запаздывания к периоду квантования.
- •5.4. Рекомендации по практическому применению регуляторов с наблюдающими устройствами
- •5.5. Автоматическая система дозирования аммиака в питательный тракт воды парового котла
- •Заключение
- •Библиографический список
4.2. Астатический оптимальный по быстродействию регулятордля объекта первого порядка с запаздыванием
4.2.1 Структурная схема оптимального по быстродействию регулятора для объектов первого порядка с запаздыванием.
Используя обобщенную схему рис.4.1 можно разработать структурную схему (рис.4.2) астатического оптимального по быстродействию регулятора с наблюдателем, работающего с моделью первого порядка с запаздыванием.
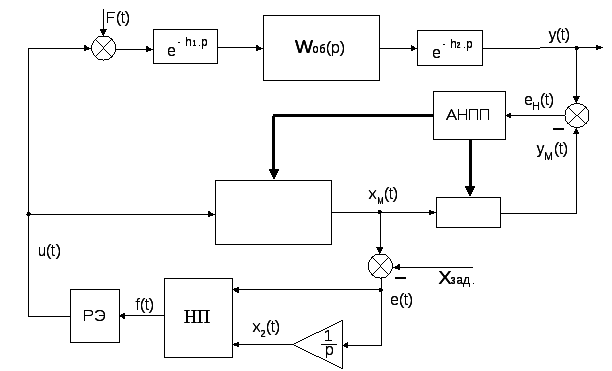
Рис.4.2. Структурная схема оптимального по быстродействию регулятора для объектов 1-ого порядка с запаздыванием
В схеме обозначены: НП – нелинейный преобразователь; РЭ – релейный элемент. В ней, для придания регулятору астатизма по сигналам задания и возмущения введена в канал ошибки модель интегрирующего звена. Это повышает порядок эквивалентного объекта (инерционное + интегрирующее звено) до двух. Отсутствие запаздывания в эквивалентном объекте позволяет применить известные непрерывные алгоритмы оптимального управления таким объектом [28]. В нашем случае этот алгоритм будет иметь вид
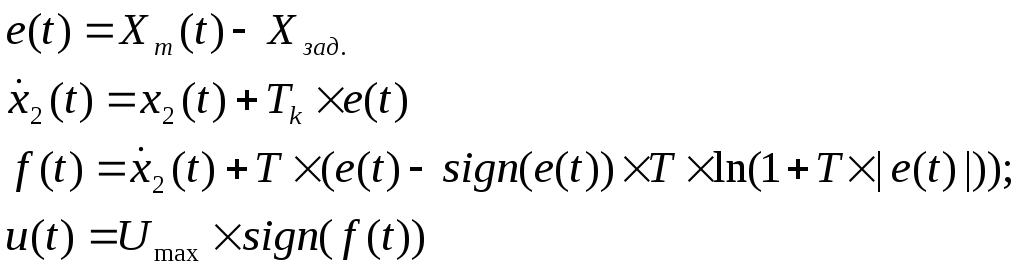 (4.1)
(4.1)
где: Т - постоянная времени передаточной функции модели объекта; Тк- период квантования; Umax=100%; f(t) - функция переключения релейного элемента РЭ.
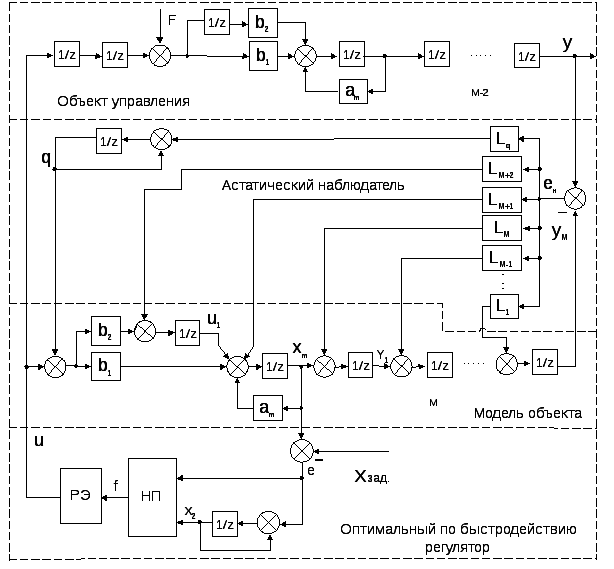 Рис.4.3.
Структурная схема оптимального по
быстродействию регулятора в цифровом
виде.
Рис.4.3.
Структурная схема оптимального по
быстродействию регулятора в цифровом
виде.
Реализация такой структуры в аналоговом варианте представляет большие сложности. Ниже предлагается квазиоптимальный алгоритм цифровой реализации предложенного регулятора. Ясно, чем меньше период квантования, тем ближе качество переходных процессов к оптимальным по быстродействию и тем меньше амплитуда автоколебаний, вызванных эффектом квантования процессов по времени.
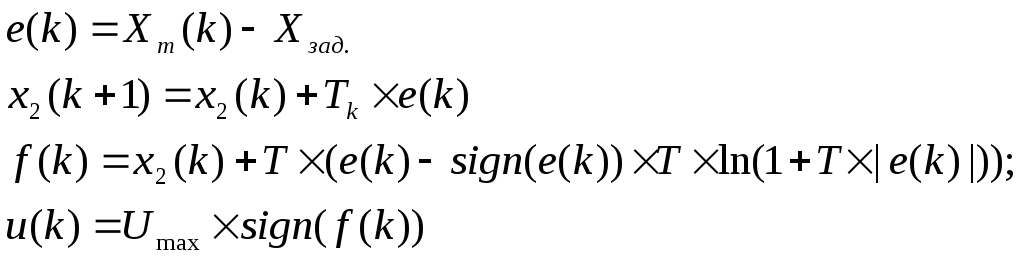 (4.2)
(4.2)
На рис.4.3. показана структурная схема цифровой оптимальной по быстродействию системы управления для случая произвольного значения задержки М.
В соответствии с [28,16] методика расчета коэффициентов астатического цифрового наблюдателя основана на принципе разделения и теории модального цифрового управления. Выше, в разделе 2.4 мы уже описали методики расчета параметров наблюдателя. Приведем лишь окончательный результат. Так, рекуррентные формулы коэффициентов астатического цифрового наблюдателя полного порядка введется последующим
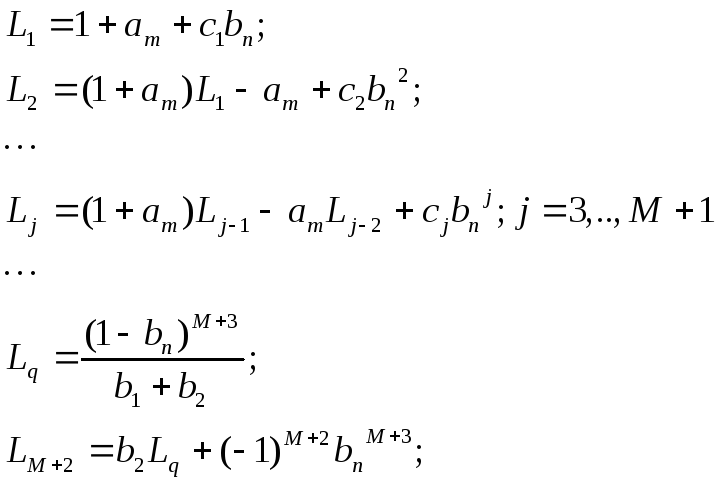 (4.3)
(4.3)
где
![]() ;
;![]() -
число сочетаний из М+3 по j; j=3…M+1.
-
число сочетаний из М+3 по j; j=3…M+1.
4.2.2. Исследование динамики системы управления модального регулятора со статическим наблюдателем для объектов первого порядка с запаздыванием
На Рис.4.4 приведены графики отработки сигналов задания и возмущения в оптимальной по быстродействию цифровой системе управления.
В качестве объекта управления использована цифровая модель третьего порядка с параметрами К0=1; Т1=420с; Т2=0.01с;. Т3=0,004с; τ0=100с. В регуляторе используется эквивалентная модель первого порядка с параметрами Км=1, Тм=400 с, τм=100 с. Период квантования Тк=2с.
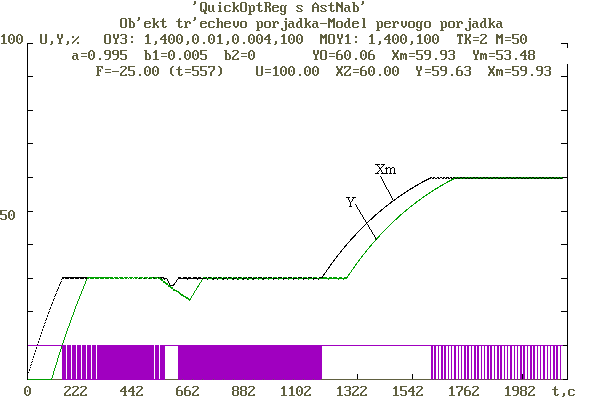
Рис.4.4. Графики отработки сигналов задания и возмущения.
В нижней части графика показано изменение управляющего сигнала, который принимает только 2 значения – 0 и 100 %. В установившемся режиме управление наблюдается процесс переключения релейного элемента с высокой частотой, что обеспечивает весьма малую (меньше 0,1%) амплитуду колебания выходного сигнала. В тоже время отработка сигналов задания и возмущения происходит без статической ошибки.
4.3. Оптимальный по быстродействию регулятор для объектов второго порядка с запаздыванием.
4.3.1 Структурная схема оптимального по быстродействию регулятора для объектов второго порядка с запаздыванием.
Аналогично предыдущему случаю, будем использовать непрерывный алгоритм оптимального управления объекта второго порядка. Соответствующая структурная схема оптимальной по быстродействию системы управления с наблюдателем приведена на рис.4.5.
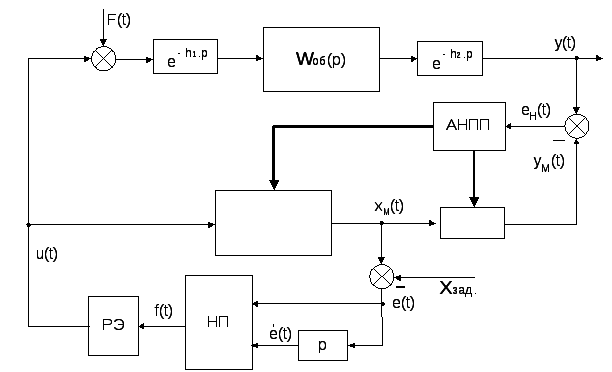
Рис.4.5. Структурная схема оптимального по быстродействию регулятора для объектов 2-ого порядка с запаздыванием
Непрерывные алгоритмы оптимального управления в этом случае, по [6], имеет вид
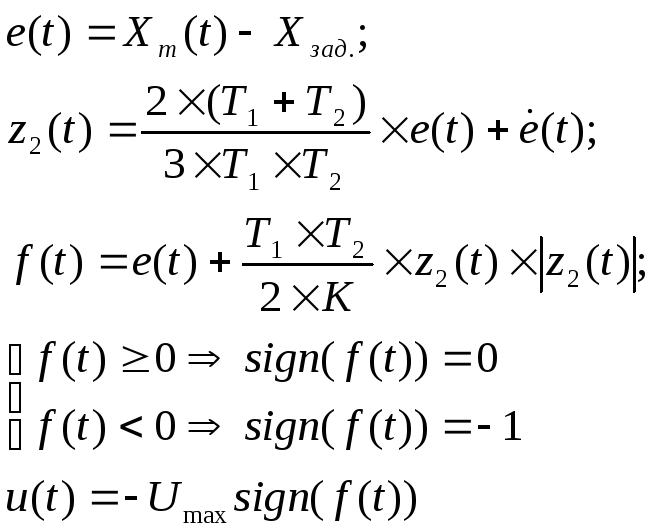 (4.4)
(4.4)
На рис.4.6. показана структурная схема цифровой оптимальной по быстродействию системы управления для произвольной задержки М.
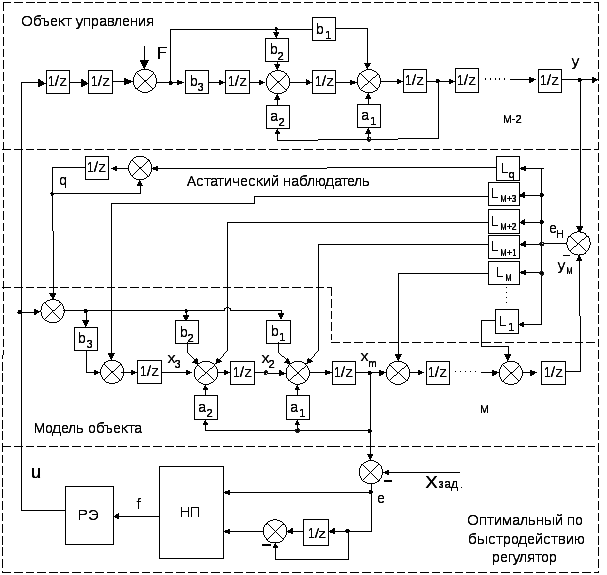
Рис.4.6. Структурная схема оптимального по быстродействию регулятора для управления объектов 2-ого порядка в цифровом виде.
Приведем алгоритм цифровой реализации регулятора
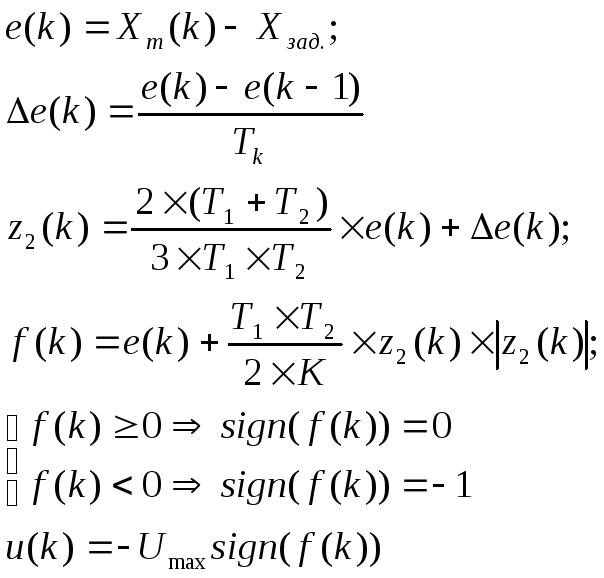 (4.5)
(4.5)
Как и в предыдущем случае из результатов, полученных выше в разделе 3.3. приведем рекуррентные формулы для коэффициентов наблюдателя
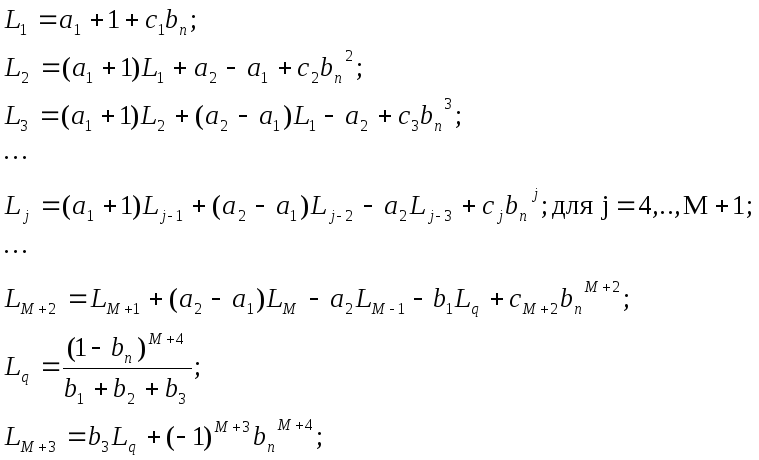 (8)
(8)
где
![]() ,а
,а ![]() -
число сочетаний из М+4 по j, j=1,2…M+2.
-
число сочетаний из М+4 по j, j=1,2…M+2.
