1.3. Обзор методов синтеза регуляторов для объектов управления с запаздыванием

В настоящее время известно несколько методов синтеза оптимальных по быстродействию систем управления объектами с запаздыванием [6]. Широко применяют метод, основанный на компенсации временного запаздывания в оптимальных системах по методу Р.Бэсса. Сущность его состоит в том, что для компенсации запаздывания в оптимальных системах при построении функции аргумента управления вносится упреждение на  с тем, чтобы управляющее воздействие системы с запаздыванием и той же системы без запаздывания совпадали. В математической интерпретации это означает, что в фазовом пространстве поверхность управления, упреждающая по времени на  поверхность переключения, строится по заданной поверхности переключения той же системы без запаздывания.

Координаты состояния компенсированной системы могут быть представлены в виде линейных комбинаций текущих координат, весовые коэффициенты которых зависят от времени запаздывания. Отсюда следует, что нелинейный устройства, реализующие оптимальный алгоритм в системе с запаздыванием, может оставаться тем же, что и в системе без запаздывания, если на его входы вместо текущих значений координатподавать их линейные комбинации.

Можно дать в общем виде следующую геометрическую интерпретацию метода Бэсса. Пусть уравнение оптимальной поверхности переключения при отсутствии запаздывания в системе известно и имеет вид:

(1.12)

Считая, что функция Ф разрешима относительно одного из своих аргументов х₁, х₂... х_n , например х₁, запишем (1.12) как

(1.13)

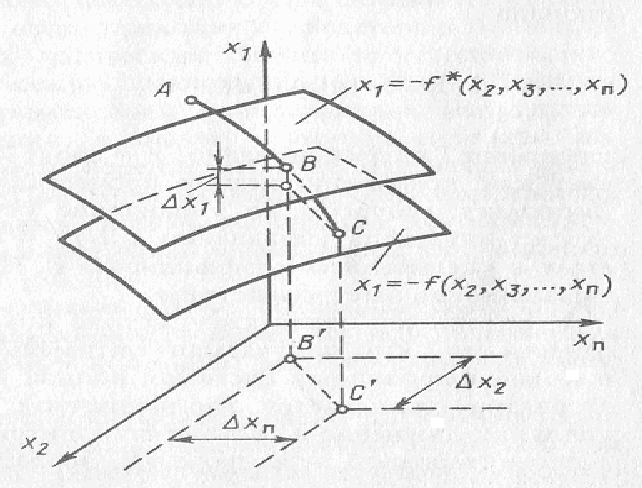
Рис. 1.1. Геометрическая интерпретация метода Бэсса

Если же в системе имеется запаздывание , то оптимальная поверхность в этом случае представляет собой геометрическое место точек, из которых через время  при вынужденном движении системы изображающая точка переходит на поверхность (1.13). Уравнение оптимальной поверхности переключения компенсированной системы в этом случае имеет вид

(1.14)

или

(1.15)

Если обозначить расстояние между проекциями точек В и С на осях х₁, х₂... х_n через х₁,х₂,...,х_n соответственно, то не трудно заметить, что х_{i ,} i= являются функциями времени запаздывания, а величины ,i= - значениями координат, характеризующими состояние системы через время.

Из геометрических соображений имеем

(1.16)

или

(1.17)

Уравнение (1.12), (1.13) является общим для определение Ф* по заданной функции Ф. Для этого достаточно определить величины х_i ()_, i= , а затем подставить будущие значения координат системых_i+х_i в уравнение поверхности переключения системы без запаздывания.

К основному недостатку метода компенсации запаздывания следует отнести то, что получаемая оптимальная поверхность переключения в компенсированных системах в близи начала координат фазового пространства оказывается неоднозначным. При определенных начальных условиях движение в системе становится неоптимальным: увеличивается число интервалов переключения, возрастает время переходного процесса, при этом отклонение фазовой траектории от оптимальной может быть существенным и различным, но оценить его заранее сложно. Избавиться от этого недостатка можно лишь путем использования при синтезе оптимальных систем специальных подходов.

Компенсация запаздывания по методу Бэсса без нарушения оптимальности фазовой траектории возможна только в том случае, когда область, в которой система теряет признаки оптимальной, равна нулю для каждого интервала управления. Это требование равнозначно условию:

t_j _, j= (1.18)

где t_j – длительность j – го интервала управления.

Существует метод, суть которого заключается в искусственном увеличении интервалов управления с длительностью t_j . Задача сводится к нахождению на этих интервалах такой функции управления , реализация которой обеспечиваетt_j=  при тех же начальных и конечных условиях для фазовых координат на этих интервалах, найденных для оптимального управления без компенсации.

Таким образом, при компенсации запаздывания в оптимальных системах по методу Бэсса к обычным ограничениям по фазовым координатам управляющему воздействию необходимо еще добавлять ограничения вида (1.18). Это обстоятельство приводит к введению в оптимальный регулятор дополнительных логических блоков и устройств, что существенно усложняет техническую реализацию системы. Поэтому на практике ограничиваются применением приближенных (квазиоптимальных) алгоритмов управления, в основу которых положено линейная аппроксимация поверхности переключения вблизи начала координат фазового пространства. При этом полностью скомпенсировать влияние запаздывания на динамику системы не удается, хотя амплитуда возникающих автоколебаний значительно уменьшается по сравнению с некомпенсированной системой.

Другой подход к синтезу оптимальных по быстродействию систем управления объектами с запаздыванием основан на использовании в законе управления прогнозируемых координат регулируемой величины и ее производных. Рассмотрим задачу прогнозированного оптимального по быстродействию управления системой, неизменная часть которой состоит из звена запаздывания, интегрирующего и апериодического звеньев, включенных последовательно. В основу предлагаемого метода синтеза положен оптимальный по быстродействию закон управления подобной системой без запаздывания, в котором вместо текущих координат объекта используется их прогнозируемые значения. При этом последние определяются путем решения относительно фазовых координат (при известных начальных условиях) уравнение, описывающего состояние системы без учета запаздывания.

Недостатком этого метода является необходимость моделирования запаздывания и проведение операций дифференцирования, а также большое число настроечных элементов. Кроме того, при управлении объектами с небольшим самовыравниванием некоторые коэффициенты принимают недопустимо большие значения, поэтому рекомендуется при реализации системы сигнал по производной от регулируемой величины в законе управления не использовать. В этом случае управляющее воздействие регулятора является функцией лишь двух сигналов – сигнала от регулируемой величины и сигнала дополнительной нелинейной динамической обратной связи. Как показали исследования, применение такого регулятора позволяет примерно в два раза увеличить быстродействие системы.

Рассмотрим объект управления, описываемый уравнением вида

a=u(t-) (1.19)

а оптимальный по быстродействию регулятор – уравнением

u(t)= - Umax sign(+) (1.20)

где прогнозируемые координаты получены через текущие значения координат объекта управленияи

(1.21)

Показано [6], что для обеспечения устойчивости в такой системе в передаточных функциях

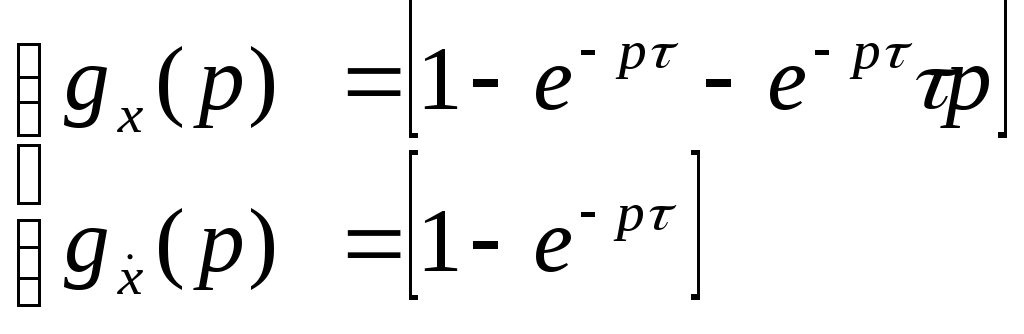(1.22)

необходимо иметь идеальное звено запаздывания и дифференциатор.

Для объектов, описываемых уравнениями вида:

(1.23)

передаточные функции оптимальной системы идолжны также состоять из идеальных звеньев запаздывания и дифференцирования, реализация которых весьма затруднительна. Однако передаточные функциииможно легко реализовать, если использовать логический блок, формирующий импульс длительностью и дельта–функцию, умноженную на . При этом, для формирования импульса длительностью  необходимо иметь реле времени, а для формирования дельта-функции – импульсное устройство. В качестве управляемых моделей иможно использовать пассивные и активныеRC – фильтры. В случае управления объектом n-го порядка с запаздыванием логический блок должен при переключениях управления формировать n импульсов для управления соответствующими моделями. Согласно результатам исследования предложенный метод реализации оптимального по быстродействию прогнозируемого управления позволяет уменьшить амплитуду возникающих в системе с запаздыванием автоколебаний примерно в 3- 4 раза.

Также для оптимального управления линейными объектами с запаздыванием используются итерационные методы и, в частности, управление с прогнозированием на быстродействующих аналоговых машинах. Отличительная особенность такого подхода – получение в ускоренном масштабе времени будущих состояний системы и выбор на их основании оптимальных управляющих воздействий. В момент переключения в системе устанавливается прохождением одной из семейства прогнозируемых траекторий через начало координат фазовой плоскости, что фиксируется логическим устройством, выдающим команду на реверс объекта. Таким образом, если компенсация временного запаздывания по методу Бэсса осуществляется упрежденным на  реверсированием системы (что практически трудно выполнимо в силу неоднозначности новой линии переключения), то в предлагаемой системе запаздывание компенсируют изменением граничных условий, на соответствие которым проверяются прогнозируемые фазовые траектории.

Рассмотрим метод синтеза оптимальных по быстродействию систем управления объектами с запаздыванием, предложенный А.Т.Фуллером. Рассмотрим линейные объекты, содержащие звенья чистого запаздывания в канале управления. Уравнение исследуемых объектов

(1.24)

где А и В – матрицы состояния и управления размерностью n*n и 1*m соответственно;

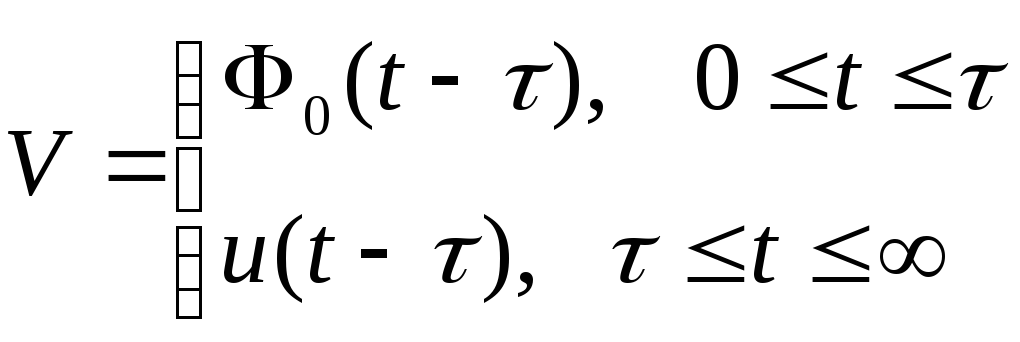(1.25)

– выход звена запаздывания; Ф₀(t) – начальная функция; u(t) – скалярное управление.

При отсутствии запаздывания оптимальное управление представляет собой функцию координат состояния этой системы

u(t)= - sign f(х₁(t), х₂(t),...,х_n(t)) , <∞ (1.26)

При наличии запаздывания оптимальное управление есть функция упрежденных на время τ координат состояния объекта

u(t)= - sign f(х₁(t+ τ), х₂(t+ τ),...,х_n(t+ τ)) (1.27)

Эта функция имеет такой же вид, как и при отсутствии запаздывания. Таким образом, для определения оптимального управления системой необходимо выразить упрежденные значения х₁(t+), х₂(t+),...,х_n(t+) через текущие координаты состояния. При этом исходят из того условия, что величина Х(t+) есть отклик системы во время t +  на вход v(t+S), 0S <  и начальные условия х₁(t), х₂(t),...,х_n(t) , который в матричной форме записи может быть представлен в виде:

X(t+)=е^Aт Х(t)+е^А(t-S)BW(t-+S)dS (1.28)

На основании вышеизложенного получают:

u(t)= - sign f е^Aт Х(t)+е^А(t-S)BW(t-+S)dS (1.29)

где функция W(t-+S) описывает динамическое состояние звена чистого запаздывания, причем для интервала времени < ∞

W(t-+S) = u(t-+S), 0S <  (1.30)

для интервала 0t < 

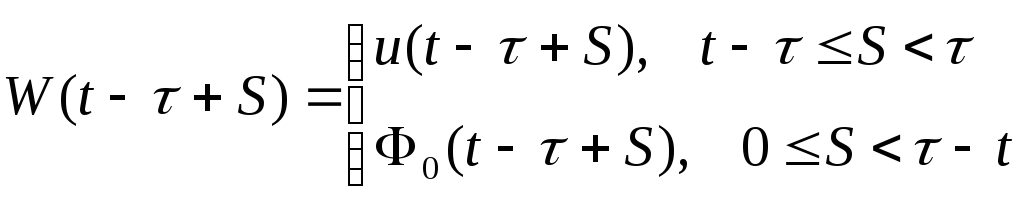(1.31)

Здесь S – распределенный параметр звена запаздывания;

Ф₀(t-+S) - начальная функция, распределенная по звену запаздывания.

Однако чтобы осуществить техническую реализацию оптимального закона вида (1.31) необходимо формировать дополнительные сигналы, определяемые функционалом

е^А(t-S)BW(t-+S)dS (1.32)

В некоторых условиях это выполнимо, часто же измерить состояние запаздывания оказывается вообще невозможным, поэтому предлагается использовать в регуляторе модель запаздывания. Входом в модель является выход с регулятора u(t). Регулятор измеряет состояние запаздывания модели вместо состояния запаздывания объекта. Аналитически введение модели запаздывания равносильно замене функционала (1.32) на функционал вида:

е^А(t-S)Bu(t-+S)dS (1.33)

В течение первого интервала длительностью  состояния запаздывания объекта и запаздывания объекта не одинаковы, так что управление на данном интервале не оптимально. Для t >  состояние запаздывания модели и состояние запаздывания объекта совпадают и, таким образом, управление оптимально после первого интервала запаздывания. В общем, управление квазиоптимально. При этом проблема формирования функционалов состояния запаздывания модели все еще имеет существенные трудности, хотя технически не так сложна, как для запаздывания объекта. Учитывая это, предлагается другой метод приближенной реализации оптимального закона вида (1.27) и (1.28). Сущность его состоит в том, что линейный функционал (1.33) определяется путем пропускания сигнала u(t) через фильтр с векторной передаточной функцией вида:

(1.34)

где g(p) – векторная передаточная функция объекта.

Для технической реализации f(p) необходимо иметь модель объекта, блок запаздывания и множительный блок с коэффициентом e^A. Схема квазиоптимальной системы управления в этом случае близка к схеме упредителя Смита и имеет общие с ним недостатки, заключающиеся в том, что не учитывается начальная функция звена запаздывания и требуется достаточно точное моделирование звена запаздывания в регуляторе.

Можно сделать вывод, что синтез строго оптимальных по быстродействию законов управления для линейных объектов с запаздыванием приводит в большинстве случаев к схемам оптимальных регуляторов, реализация которых в реальных условиях или невозможна, или совершенно нецелесообразна ввиду значительных затрат и сложности аппаратурного оформления.

В книге [6] авторы предложили методы синтеза квазиоптимальных по быстродействию алгоритмов, позволяющие построить регуляторов для промышленных объектов с запаздыванием. Был предложен метод, основан на аппроксимации функциональных составляющих оптимального закона произвольным числом отрезков. Линейная аппроксимация позволяет получить квазиоптимальный алгоритм управления в явном виде и довольно просто разработать схему квазиоптимальной по быстродействию системы. В книге описаны процедуры получения квазиоптимальных по быстродействию законов управления для объектов с запаздыванием, как в управляющих, так и в промежуточных координатах.

Наиболее часто используются принципы построения и методики синтеза оптимальных регуляторов для объекта с запаздыванием, основанные на методе упреждения координат вектора состояния. Суть его заключается в том, что оптимальный закон управления в системе с запаздыванием формируется при тех же значениях коэффициентов регулятора, что и для системы без запаздывания, но с использованием упрежденного вектора состояния.

Главным недостатком структуры с упредителем является увеличение ошибки прогнозирования координат вектора состояния при малых периодах квантования в связи с неточностью модели и увеличением числа циклов решения системы уравнения.