4.5. Определение возмущений и начальных условий в напряжениях.

Для определения возмущений в напряжениях достаточно воспользоваться уравнением преобразования (4.2):

. (4.16)

Если возмущение представляет заданную функцию времени, то

(4.17)

Напряжение можно воспроизвести путём решения некоторого вспомогательного уравнения или с помощью вариатора коэффициентов. В последнем случае напряжениецелесообразно представить в виде уравнения

(4.18)

где

(4.19)

(4.20)

Коэффициент изменяется отдои реализуется с помощью вариатора коэффициентов. Графикполучается из графика, как показано на рис. 4.4.

При определении начальных напряжений могут представиться два случая: 1) масштабы преобразования всех переменных и их производных известны, 2) масштабы преобразования производных неизвестны.

В первом случае для определения начальных напряжений достаточно воспользоваться уравнением преобразования (4.2):

(4.21)

Во втором случае необходимо получить уравнения для определения начальных напряжений, соответствующих производным. Для этого по структурной схеме модели для каждого интегрирующего усилителя (кроме интегрирующего усилителя, на который подается напряжение, соответствующее старшей производной) составляют уравнение, связывающее выходное и входное напряжения.

Используя уравнения (4.13), в качества примера получим уравнения для определения начальных напряжений, соответствующих производным.

(4.22)

Лекция № 26. План.

1. Подготовка нелинейного дифференциального уравнения к решению на АВМ.

2. Составление схемы модели.

З. Расчет коэффициентов передач.

4.6. Особенности подготовки нелинейного дифференциального уравнения к решению на авм.

Подготовка нелинейного дифференциального уравнения производится, в основном, так же, как и подготовка линейного дифференциального уравнения. При этом в заданном уравнении целесообразно выделить произведения и частные переменных, нелинейные функции и аргументы трансцендентных и неаналитических функций.

Рассмотрим пример подготовки нелинейного дифференциального уравнения. Пусть для решения на АВМ задано нелинейное дифференциальное уравнение 4–го порядка с постоянными коэффициентами:

(4.23)

Выделяем в уравнении (4.23) произведение и частное переменных, нелинейные функции и аргумент трансцендентной или неаналитической функции:

Получаем систему машинных уравнений:

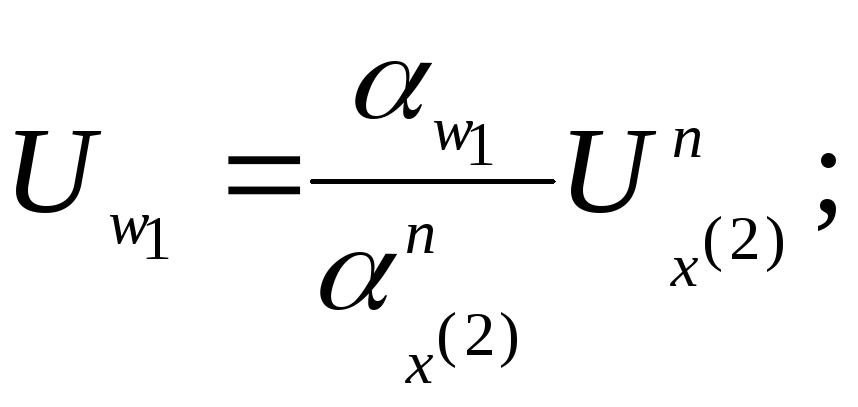
Составляем структурную схему модели (рис. 4.5). Выразим коэффициенты передачи нелинейных решающих элементов через масштабы преобразования переменных.

По структурной схеме (рис. 4.5) для каждого нелинейного решающего элемента составляем уравнение, связывающее выходное и входное напряжения:

(МУ)

(ДУ)

(ФП № 1)

(ФП № 2)

Сопоставляя полученные уравнения с соответствующими машинными уравнениями, выражаем коэффициент передачи нелинейных решающих элементов через масштабы преобразования переменных:

(4.24)

Анализируя уравнения (4.24) и структурную схему (рис. 4.5), можно сформулировать следующие правила, позволяющие выразить коэффициенты передач нелинейных решающих элементов через масштабы преобразования переменных:

1) коэффициент передачи множительного устройства равен масштабу преобразования произведения, деленному на произведение масштабов преобразования сомножителей;

Рис. 4.4

рис. 4.5

2)коэффициент передачи делительного устройства равен произведению масштабов преобразования частного и делителя, делённому на масштаб преобразования делимого;

3)коэффициент передачи функционального преобразователя, воспроизводящего n–ю степенную функцию, равен масштабу преобразования функции, делённому на масштаб преобразования аргумента в степени n;

4)коэффициент передачи функционального преобразователя, воспроизводящего трансцендентную или неаналитическую функцию, равен масштабу преобразования функции.

Получим соотношения между коэффициентами передачи решающих элементов, масштабами преобразования переменных и коэффициентами исходного уравнения.

По структурной схеме (рис. 4.5) для каждого решающего элемента составляем уравнение, связывающее выходное и входные напряжения.

(№6) , (4.25)

(МУ)

(ДУ) (4.26)

(ФП № 1)

(ФП № 2)

(№ 4) (4.26а)

(№ 1)

(№ 2)

(№ 3)

Из уравнений (4.25), (4.26) и (4.26а) исключаем напряжения, соответствующие производным:

(№ 2)

(№ 3)

Из уравнений (4.25), (4.26) и (4.26а) исключаем напряжения, соответствующие производным:

Заменяем в уравнении (4.27) машинные переменные исходными переменными, используя уравнения преобразования (4.1а) и (4.2):

Сопоставляя полученное уравнение с исходным уравнением (4.23), получаем соотношения между коэффициентами передачи решающих элементов, масштабами преобразования переменных и коэффициентами исходного уравнения:

(4.28)

Анализируя уравнения (4.28), структурную схему (рис. 4.5) и исходное уравнение (4.23), можно сформулировать следующие правила, позволяющие получать соотношения между коэффициентами исходного уравнения при нелинейных членах, коэффициентами передачи решающих элементов и масштабами преобразования переменных.

1. Коэффициент исходного уравнения при произведении, частном или степенной функции равен произведению двух сомножителей:

а) первый сомножитель выражается так же, как и коэффициент исходного уравнения при линейном члене, причём для коэффициента при произведении берется контур, на выходе которого получается напряжение, соответствующее сомножителю большего порядка, а для коэффициента при частном берется контур, на выходе которого получается напряжение, соответствующее делимому,

б) второй сомножитель равен масштабу преобразования искомой переменной, делённому на произведение коэффициентов передачи интегрирующих усилителей, последовательно включенных в цепь между второй точкой подключения обратной связи и выходом искомой переменной, и на масштаб времени в степени, равной числу интегрирующих усилителей в этой цепи;

в) второй сомножитель возводится в степень N, причём для коэффициента при произведении N=1, для коэффициента при частном N=-1, для коэффициента при степенной функции N=n-1.

2. Коэффициент исходного уравнения при трансцендентной или неаналитической функции выражается так же, как и коэффициент исходного уравнения при независимой переменной (внешнем возмущении) y(t).

3. Коэффициент исходного уравнения при переменной аргумента трансцендентной или неаналитической функции равен произведению двух сомножителей:

а) первый сомножитель равен отношению коэффициента передачи масштабного усилителя, на выходе которого получается напряжение, соответствующее аргументу функции, к масштабу преобразования аргумента функции;

б) второй сомножитель равен масштабу преобразования исходной переменной, делённому на произведение коэффициентов передачи интегрирующих усилителей, последовательно включенных в цепь между точкой подключения обратной связи и выходом искомой переменной, и на масштаб времени в степени, равной числу интегрирующих усилителей в этой цепи.