§12. Полный четырехвершинник на проективной плоскости

Определение. Полным четырехвершинником называется фигура, состоящая из четырех точек – вершин проективной плоскости, никакие три из которых не лежат на одной прямой; и шести прямых – сторон, попарно соединяющих вершины.

Стороны, не имеющие общей вершины, называются противоположными. Точки пересечения противоположных сторон называются диагональными.

Н а рисунке 10 изображен четырехвершинник ABCD, где A, B, C, D – вершины; (AB) и (CD), (BC) и (AD), (BD) и (AC) – пары противоположных сторон; E, F, G – диагональные точки.

Можно легко доказать, что диагональные точки полного четырехвершинника не лежат на одной прямой.

Рассмотрим подробнее фигуру, определяемую полным четырехвершинником.

Прямые, попарно соединяющие диагональные точки, называются диагоналями. На рисунке 10 диагонали изображены пунктиром.

Следующая теорема показывает, что полный четырехвершинник содержит в себе гармонические четверки точек и прямых.

Теорема. На каждой диагонали полного четырехвершинника диагональные точки гармонически разделяют две точки, в которых эта диагональ пересекает стороны, проходящие через третью диагональную точку.

(GF, KL) = –1.

Следствие 1. Две вершины, лежащие на стороне полного четырехвершинника, гармонически разделяют пару точек, состоящую из диагональной точки и точки, в которой эта сторона пересекает диагональ, проходящую через другие диагональные точки.

Следствие 2. Две противоположные стороны полного четырехвершинника гармонически разделяют две диагонали, проходящие через точку пересечения этих сторон.

Условимся называть точу Х четвертой гармонической к трем данным точкам А, В, С, если (АВ, СХ) = –1.

Задача 30. На аффинной (или евклидовой) плоскости задан отрезок [AB] и его середина С. Пользуясь только линейкой без делений, провести прямую через данную точку D, не принадлежащую прямой (АВ), параллельно этой прямой.

Задача 31. Даны две различные параллельные прямые. Пользуясь только линейкой, построить середину отрезка, заданного на одной из данных прямых.

Задача 32. На аффинной (евклидовой) плоскости задан параллелограмм (окружность с центром), прямая m и точка А. С помощью одной линейки через точку А провести прямую, параллельную прямой m.

Задача 33. Построить четвертую гармоническую точку Х к трем данным точкам А, В, С, лежащим на одной прямой.

§13. Проективные отображения прямых и пучков

Допустим, что две прямые g и g принадлежат одной проективной плоскости. Взаимно однозначное отображение всех точек прямой g на множество точек прямой g называется проективным, если оно сохраняет сложное отношение четырех точек.

Имеет место следующая теорема.

Теорема. Биекция f:gg прямой g на прямую g является проективным отображением, если и только если, каждый проективный репер  прямой g переходит в проективный репер  прямой g и выполняется правило равенства координат: прообраз – точка M(x¹, x²) на прямой g имеет такие же координаты в репере , что и образ – точка M (x¹, x²) в репере  на прямой g.

П римером проективного отображения одной прямой на другую служит перспектива. Пусть g и g – две различные прямые проективной плоскости, и точка O, называемая центром перспективы, не лежит на этих прямых. Каждой точке M прямой g ставится в соответствие проекция M на прямой g из центра O.

Критерий перспективности. Для того, чтобы проективное отображение f:gg было перспективным, необходимо и достаточно, чтобы точка пересечения прямых g и g переходила в себя.

Теорема. Проективное отображение одной прямой на другую есть композиция не более двух перспектив.

Приведем иллюстрацию к этой теореме.

Задача 34. В проективном отображении f:gg репер =(A, B, C) переходит в репер =(A, B, C). Построить образ произвольной точки M прямой g.

Решение.

П роведем прямую (AA) и отложим на ней два центра перспективы O и O, отличные от точек A и A. Пусть B=(OB)(OB), C=(OC)(OC), g=(B, C), A=(OO)g. Тогда перспектива f_O с центром в точке O переводит репер  в репер =(A, B, C) на прямой g, а перспектива f_O с центром в точке O переводит репер  в репер , таким образом f=f_Of_O. Далее находим точку M на прямой g: M=(OM)g, и, наконец, M=(OM)g.

Теорема. Проективное преобразование прямой на себя есть композиция не более трех перспектив.

Задача 35. В проективном преобразовании f:gg прямой g на себя заданный репер =(A, B, C) переходит в заданный репер =(A, B, C). Построить образ и прообраз произвольной данной точки M на g.

Двойственным образом строится теория проективных отображений пучков прямых на проективной плоскости.

Определение. Взаимно однозначное отображение пучка на пучёк называется проективным, если оно сохраняет сложное отношение четырех прямых.

Теорема. Если a, b, c – три произвольные прямые пучка с центром в точке O и a, b, c – три произвольные прямые пучка с центром в точке O, то существует одно и только одно проективное отображение пучка O на пучок O, переводящее прямые a, b, c в прямые a, b, c.

Р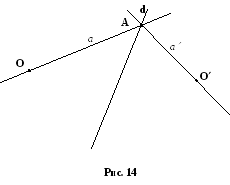 ассмотрим пучки с центрами в двух точках O и O и прямую d, не проходящую через точки O и O. Каждой прямой a пучка O поставим в соответствие прямую a пучка O, которая проходит через точку пересечения прямых a и d.

Построенное отображение является проективным и называется перспективным. Прямая d называется осью перспективы.

Критерий перспективности. Для того, чтобы данное проективное отображение пучка на пучок было перспективным, необходимо и достаточно, чтобы прямая, проходящая через центры пучков, переходила в себя.

Задача 36. В проективном отображении f пучка O на пучок O три попарно различные прямые a, b, c переходят соответственно в прямые a, b, c. Построить образ произвольной прямой m пучка O.

Решение.

Через точку A пересечения прямых a и a проведем две прямые d и d, отличные от прямых a и a, и обозначим через B и C точки пересечения прямых b и c с прямой d, а через B и C точки пересечения прямых b и c с прямой d. Отображение f порождает перспективу прямой d на прямую d с центром в точке S=(BB)(CC).

Д ля построения образа произвольной прямой m находим сначала точку М, как пересечение прямых m и d, далее строим M=(SM)d. Прямая (OM) – искомая.