=135=

	МИНИСТЕРСТВО ОБРАЗОВАНИЯ МОСКОВСКОЙ ОБЛАСТИ МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ОБЛАСТНОЙ УНИВЕРСИТЕТ
	ИСАЕВА М.А., МАРТЫНЮК А.Н., МАТВЕЕВ О.А., ПТИЦЫНА И.В. ВВЕДЕНИЕ В ДЕЙСТВИТЕЛЬНУЮ ПРОЕКТИВНУЮ ГЕОМЕТРИЮ УЧЕБНОЕ ПОСОБИЕ МОСКВА 2010

УДК 513.7

ББК 22.151.3

П - 87

Печатается по решению кафедры математического анализа и геометрии Московского государственного областного университета

Исаева М.А., Мартынюк А.Н., Матвеев О.А., Птицына И.В.

Введение в действительную проективную геометрию. Учебное пособие. – М.: Издательство МГОУ, 2010, 135с.

Основой пособия послужили лекции по проективной геометрии, прочитанные авторами на физико-математическом факультете Московского государственного областного университета. Построение всех конструкций в проективном пространстве опирается на схему Германа Вейля. Несмотря на общий стиль изложения авторы стремились подчеркнуть связь проективной геометрии со школьным курсом геометрии, с идеями олимпиадных школьных и студенческих задач.

Рецензенты:

доктор физико-математических. наук, профессор Богданов Д.Л.,

доктор педагогических. наук, профессор Жаров В.К.

СОДЕРЖАНИЕ

1

МИНИСТЕРСТВО ОБРАЗОВАНИЯ МОСКОВСКОЙ ОБЛАСТИ 1

МОСКВА 1

2010 1

СОДЕРЖАНИЕ 3

ПРЕДИСЛОВИЕ 5

ГЛАВА 1. ПЕРВОНАЧАЛЬНЫЕ ПОНЯТИЯ, ОПРЕДЕЛЕНИЯ, ФАКТЫ. 6

§1. Возникновение проективной геометрии. Центральное проектирование 6

§2. Понятие проективного пространства. Простейшие свойства 8

§3. Модели проективного пространства 12

§4. Понятие проективных координат 14

§5. Проективные координаты на плоскости 16

§6. Уравнение прямой на проективной плоскости 18

§7. Преобразование проективных координат 21

§8. Принцип двойственности 24

ГЛАВА 2. НЕКОТОРЫЕ ЛИНЕЙНЫЕ ОБРАЗЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ 25

§9. Теорема Дезарга 25

§10. Сложное отношение четырех точек прямой 30

§11. Сложное отношение четырех прямых пучка проективной плоскости 32

§12. Полный четырехвершинник на проективной плоскости 34

§13. Проективные отображения прямых и пучков 36

§14. Теорема Паппа 40

§15. Преобразования проективной прямой. Инволюции. 41

§16. Преобразования проективной плоскости. Гомологии. 43

ГЛАВА 3. ЛИНИИ ВТОРОГО ПОРЯДКА НА ПРОЕКТИВНОЙ ПЛОСКОСТИ 45

§17. Понятие проективной линии второго порядка 45

§18. Проективная классификация линий второго порядка. 47

§19. Пересечение проективной линии второго порядка с прямой. Касательная к линии второго порядка. 48

§20. Полюс, поляра, поляритет. 49

§21. Теорема Штейнера. 54

§22. Теоремы Паскаля и Брианшона . 56

Рис. 25 63

Связь между проективными и аффинными координатами. 64

Геометрия аффинной плоскости с проективной точки зрения. 64

Приложение 1 67

Ответы, указания, решения задач к главам 1, 2, 3. 67

95

Основные результаты и даже большая часть методов проективной и неевклидовой геометрии для геометра так же необходимы, как дифференциальное и интегральное исчисление для аналитика. Г. Буземан, П. Келли

ПРЕДИСЛОВИЕ

В настоящем учебном пособии авторы не ставят перед собой грандиозной задачи объять необъятное, при подборе материала для изложения использовались лишь самые чистые источники проективной премудрости. В целях экономии места и, главное, усилий вдумчивого читателя некоторые красивые цепочки теорем представлены основными фактами без достаточного обоснования, но со ссылками на соответствующую литературу.

Основой вводного курса в проективную геометрию послужили лекции, прочитанные авторами на физико-математическом факультете Московского государственного областного университета. Построение общих конструкций нашего изложения основывается на определении проективного пространства в схеме Германа Вейля. От читателя требуется знать элементы линейной алгебры, то есть понятие конечномерного векторного пространства над полем действительных чисел, разложение вектора по базису, исследование систем линейных уравнений, определители второго и третьего порядков. Также необходимо знакомство с аффинными прямой, плоскостью, и многомерным пространством.

Обсуждая первичные понятия и определения, стараясь донести до студента главное в короткое аудиторное время, авторы стремились подчеркнуть связь проективной геометрии со школьным курсом геометрии, с идеями олимпиадных школьных и студенческих задач.

Большое внимание уделялось подбору и решению задач, часть из них оставлена без решений преднамеренно в целях активизации читателей. Подготовленный и искушенный геометр может сразу же перейти ко второй главе, где, как нам кажется, можно вновь испытать счастливые моменты сопереживания с классиками.

Авторский коллектив выражает благодарность, признательность и почтение инициатору этого проекта, знатоку и тонкому ценителю проективной геометрии, профессору, доктору физико-математических наук, заслуженному деятелю науки Российской Федерации Мантурову Олегу Васильевичу.

В работе над оформлением этого пособия приняли участие Щурова Альбина Николаевна и Солдатенков Роман Михайлович.

- «Неужели это новая вселенная?» - «Нет, это добрая, старая галактика наших предков» Из космических диалогов.

Глава 1. Первоначальные понятия, определения, факты. §1. Возникновение проективной геометрии. Центральное проектирование

К первой половине девятнадцатого века проективная геометрия сформировалась как самостоятельная дисциплина, объектом изучения которой стали свойства фигур и связанных с ними величин, инвариантные (не изменяющиеся) относительно того или иного проектирования. Исторически понятие проективной плоскости было создано для того, чтобы избавиться от необходимости различать случаи параллельных и пересекающихся прямых.

Становление и развитие проективной геометрии связано с именами Понселе (1788-1867), Шаля (1793-1880), Штейнера (1769-1863), Штаудта (1798-1867).

К концу девятнадцатого столетия стало ясно, что в рамках проективной геометрии создана глубокая и содержательная теория, включающая в единую схему геометрии Евклида, Лобачевского и Римана.

В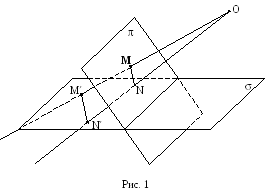 действительном трехмерном евклидовом пространстве рассмотрим две плоскости и , а также точку О, не лежащую на этих плоскостях (рисунок 1). Произвольной точке М из первой плоскости сопоставим точку M пересечения прямой ОМ с плоскостью , M - проекция точки М на плоскость из центра О. Установленное таким образом соответствие между точками двух плоскостей называется центральным проектированием.

Перемещая центр проектирования в пространстве, и, изменяя положение плоскости для одной и той же фигуры на неподвижной плоскости , получаем различные проекции, при этом многие свойства исходной фигуры изменяются. Так, например, не сохраняются длины отрезков, а также величины углов, нарушается, вообще говоря, параллельность прямых. Проектируя окружность, можно получить эллипс, параболу или гиперболу. Однако, проекции трех точек, лежащих на прямой, также принадлежат одной прямой (но свойство точки лежать между двумя другими не является проективным), проекцией линии второго порядка является линия второго порядка.

Задача 1. Докажите, что при центральном проектировании между двумя пересекающимися плоскостями трехмерного евклидова (аффинного) пространства устанавливается не взаимно однозначное соответствие.

§2. Понятие проективного пространства. Простейшие свойства

Следующее определение проективного пространства принадлежит немецкому математику Герману Вейлю (1885-1955).

Определение. Пусть Vⁿ⁺¹ – векторное пространство n+1 измерений над полем R действительных чисел, а V^* – множество всех ненулевых векторов этого пространства, V^* = Vⁿ⁺¹\{0}. Непустое множество Pⁿ – называется проективным пространством n измерений (порожденным векторным пространством Vⁿ⁺¹), если задано отображение f : V^* Pⁿ, удовлетворяющее следующим условиям (аксиомам проективного пространства):

1. Отображение f – сюръективно, (т.е. любой элемент из Pⁿ имеет хотя бы один прообраз).

2. Равенство f(x) = f(y) выполняется тогда и только тогда, когда векторы x и y коллинеарны.

Элементы множества Pⁿ называются точками проективного пространства и обозначаются прописными буквами латинского алфавита: A, B, C, …,X, Y, … . Если f(x) =X, то говорят, что вектор x порождает точку X. Из аксиомы 2 следует, что множество всех векторов пространства V^*, порождающих одну точку, есть одномерное векторное подпространство без нулевого вектора.

Так как неколлинеарные векторы порождают различные точки, то действительное проективное пространство n измерений содержит бесконечное множество точек.

Замечание. Вместо поля R можно взять любое другое поле К. Можно показать, что если поле К конечно, то полученное n-мерное проективное пространство Pⁿ(K) будет состоять лишь из конечного множества точек. Кроме того, если поле заменить телом, или даже просто кольцом, то можно построить содержательную и интересную теорию.

В дальнейшем мы будем изучать в основном свойства действительного проективного пространства двух и трех измерений.

Пусть P³ – проективное пространство трех измерений, а V⁴ – четырехмерное векторное пространство над полем действительных чисел, которое порождает проективное пространство P³. Рассмотрим векторное подпространство L^k k измерений пространства V⁴, где k = 2, 3. Множество всех точек из P³, которые порождаются ненулевыми векторами подпространства L^k, называется прямой, если k = 2, и плоскостью, если k = 3. Говорят, что подпространство L^k порождает прямую (плоскость). Прямые будем обозначать малыми буквами латинского алфавита: a, b, c,…, а плоскости – малыми буквами греческого алфавита:

Так как подпространство L^k содержит бесконечное множество попарно неколлинеарных векторов, а неколлинеарные векторы порождают различные точки, то каждые действительные проективные прямая и плоскость являются бесконечными множествами точек.

Нетрудно доказать, что в трехмерном проективном пространстве существуют тройки точек, не лежащие на одной прямой, и четверки точек, не лежащие в одной плоскости.

В самом деле, пусть a, b, c, d – базис векторного пространства V, а A, B, C и D – точки, которые порождаются этими векторами. Тогда точки A, B, C и D не лежат в одной плоскости, а любые три из этих четырех точек не лежат на одной прямой. Докажем, например, что точки A, B и С не лежат на одной прямой. Предположим противное, то есть что эти точки лежат на некоторой прямой, порожденной двумерным векторным подпространством L². Тогда векторы a, b и с принадлежат L². Но это невозможно, так как эти векторы линейно независимы, и поэтому не могут быть компланарны (то есть быть параллельными одной плоскости).

Рассмотрим свойства взаимного расположения точек, прямых и плоскостей трехмерного пространства.

1⁰. Через любые две различные точки А и В проходит одна и только одна прямая.

Пусть a и b – векторы, которые порождают точки А и В. Эти векторы не коллинеарны, так как А и В – различные точки. Рассмотрим двумерное векторное подпространство L² (a, b) порожденное этими векторами. (Любой вектор из L² является линейной комбинацией векторов a и b). Прямая l есть образ подпространства L² (a, b) и, очевидно, проходит через точки А и В.

Докажем теперь, что l – единственная прямая, проходящая через точки А и В. Допустим, что l – прямая, проходящая через точки A и B, а (L²) – двумерное подпространство, которое порождает прямую l. Так как точки А и В принадлежат l, то векторы а и b принадлежат L, и поэтому L – подпространство, порожденное векторами a и b. Таким образом, L и L – одно и то же векторное подпространство, и, следовательно, прямые l и l совпадают.

Аналогично можно доказать следующие утверждения.

2⁰. Через любые три точки, не лежащие на одной прямой, проходит одна и только одна плоскость.

3⁰. Если две различные точки А и В лежат в плоскости, то и прямая (АВ) лежит в этой плоскости (т.е. каждая точка прямой (АВ) принадлежит плоскости).

Пусть W³ – трехмерное векторное пространство, которое порождает плоскость , a и b – векторы, порождающие точки А и В. При доказательстве свойства 1⁰ мы установили, что подпространство L² (a, b) порождает прямую (АВ). Так как A, B, то aW³, bW³, поэтому L² (a, b)W³.

Пусть М – произвольная точка прямой (АВ), m – вектор, порождающий эту точку. Так как mL², то mW³. Отсюда следует, что М – точка плоскости

4⁰. Любые различные две проективные прямые, лежащие в одной плоскости, пересекаются.

Пусть a и b – две прямые, лежащие в плоскости , а L, L и W – векторные подпространства, которые порождают соответственно прямые a и b и плоскость . Прямые a и b лежат в плоскости , поэтому LW, LW. Так как L и L – различные двумерные подпространства трехмерного векторного подпространства W, то их пересечением является одномерное векторное подпространство. Ненулевые векторы этого подпространства порождают проективную точку, которая, очевидно, является общей точкой прямых а и b.

Две различные прямые a и b не могут иметь более чем одну общую точку, так как через две различные точки проходит только одна прямая.

Сформулируем без доказательства еще два утверждения.

5⁰. Любая проективная плоскость и не лежащая в ней проективная прямая имеют одну и только одну общую точку.

6⁰. Любые две различные проективные плоскости имеют общую проективную прямую, на которой лежат все общие точки этих плоскостей.

Докажем, что любую плоскость трехмерного проективного пространства можно рассматривать как двумерное проективное пространство. В самом деле, пусть – произвольная плоскость проективного пространства P³. Обозначим через W³ трехмерное векторное подпространство пространства V⁴, которое порождает эту плоскость, а через W^* – множество всех ненулевых векторов подпространства W³. Рассмотрим W³ как самостоятельное трехмерное векторное пространство. Так как W^*V^* и P³, то отображение f : V^* P³ порождает отображение f₁ : W^*, которое каждому вектору x из W^* ставит в соответствие точку f(x). Очевидно, отображение f удовлетворяет аксиомам проективного пространства. Действительно, выполнение аксиомы 1 непосредственно следует из определения плоскости, а выполнение аксиомы 2 очевидно: отображение f удовлетворяет этой аксиоме, поэтому и f₁ удовлетворяет ей.

Аналогично можно доказать, что любую прямую проективного пространства двух (трех) измерений можно рассматривать как одномерное проективное пространство.

Задача 2. Пусть Z₂ – поле вычетов по модулю 2. Доказать, что проективная прямая P¹ над Z₂ содержит точно три различные точки.

Задача 3. Доказать, что проективная плоскость P² над Z₂ содержит ровно семь различных точек и ровно семь различных прямых.

Задача 4. Доказать, что на проективной плоскости над произвольным полем существуют четыре точки, из которых никакие три не лежат на одной прямой.

Задача 5. Сколько различных точек содержит произвольная прямая проективной плоскости P² над полем Z₃ вычетов по модулю 3?

Задача 6. Пусть Z_p – поле вычетов по модулю простого числа p. Доказать, что n-мерное проективное пространство Pⁿ(Z_p) состоит из точек.

Задача 7. Сколько точек содержит произвольная прямая n-мерного проективного пространства Pⁿ над полем Z_p вычетов по модулю простого числа p?

Задача 8. Каково наименьшее число точек трехмерного проективного пространства P³ над произвольным полем?