§10. Сложное отношение четырех точек прямой

Пусть на проективной прямой даны точки A, B, C, D. Поставим задачу сопоставления действительного числа упорядоченной четверке проективных точек. Если все четыре точки совпадают, то трудно ожидать решения проблемы, т.к. на проективной прямой все точки равноправны. Допустим AD, BC, AB. Если A=C, то будем считать, что сложное отношение (AB, CD) = 0. Если AC, то точки A, B, C образуют проективный репер, в котором точка D(x¹, x²) имеет определенные координаты. В этом случае положим (AB, CD)=. Часто сложное отношение называют двойным или ангармоническим.

Легко понять, что если A, B, C – попарно различные точки, а t – любое действительное число, то на данной прямой существует одна и только одна точка D такая, что (AB, CD) = t. Если на прямой даны точки D и Е, так что (AB, CD) = (AB, CE), то D = E.

Следующая теорема показывает, как вычислять сложное отношение четырех точек по их координатам в проективном репере.

Теорема. Если точки A, B, C и D, лежащие на некоторой прямой, имеют в некотором проективном репере координаты A(a¹, a²), B(b¹, b²), C(c¹, c²), D(d¹, d²), причем AD, BC, то

.

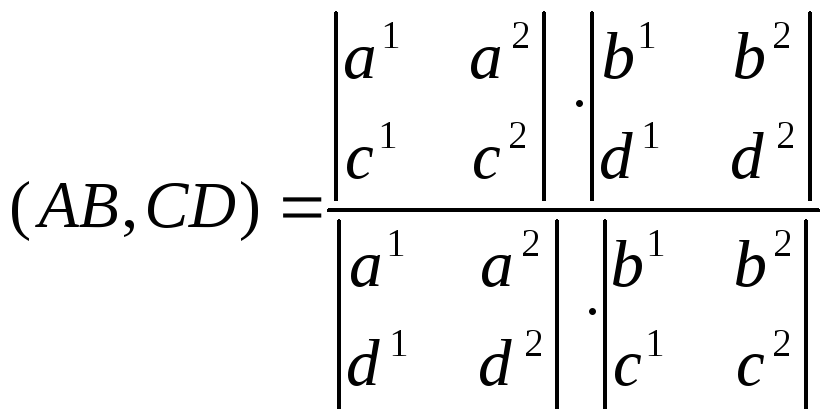Приведем простейшие свойства сложного отношения четырех точек прямой.

1. (AB, CD) = (CD, AB)

2. (AB, CD) = = , если (AB, DC)0

3. (AB, CD) = (BA, DC)

4. (AB, CC) = 1; (AB, CB) = 0

5. (AB, CD) + (AC, BD) = 1

Задача 25. Пусть A, B, C, D – четыре попарно различные точки на проективной прямой, сложное отношение которых (AB, CD) = t, где t – заданное число. Записать значения сложных отношений всех четверок точек, которые можно составить из точек A, B, C, D, переставляя их всеми возможными способами.

Задача 26. Доказать, что для пяти попарно различных точек A, B, C, D, E на проективной прямой имеет место равенство

(AB, CE) = (AB, CD)(AB, DE).

§11. Сложное отношение четырех прямых пучка проективной плоскости

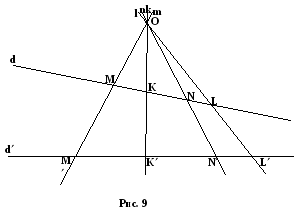
Рассмотрим две прямые d и d проективной плоскости и точку О, не принадлежащую этим прямым. Точку О примем за центр проекции. Для любой точки М на d поставим в соответствие точку M на d: M = d(OM). Точка M называется проекцией точки М из центра О, а само отображение называется проекцией.

Теорема. Проекция сохраняет сложное отношение четырех точек прямой.

( MN, KL) = (MN,KL)

Определение. Если m, n, k, l – четыре прямые на проективной плоскости, проходящие через точку О, то их сложным отношением называется сложное отношение четырех точек, высекаемых на некоторой прямой d, не проходящей через точку О.

(mn, kl) = (MN, KL)

Замечание. Определение корректно, поскольку сложное отношение четырех прямых не зависит от выбора прямой d.

Определение. Пара прямых a и b гармонически разделяет пару прямых c и d, если (ab, cd) = –1.

Задача 27. Прямые a и b евклидовой плоскости пересекаются в точке О, прямые c и d содержат биссектрисы углов, образованных прямыми a и b. Доказать, что (ab, cd) = –1.

Задача 28. Доказать, что прямые, содержащие диагонали параллелограмма, гармонически разделяют прямые, проходящие через центр параллелограмма параллельно его сторонам.

Задача 28. Доказать, что прямая (CM), содержащая медиану [CM] треугольника АВС, и прямая (CX), параллельная стороне [AB], гармонически разделяют прямые (CA) и (CB), содержащие две другие стороны треугольника АВС.