Мода и медиана в статистике

Наиболее часто используемыми в экономической практике структурными характеристиками являются мода и медиана.

Термин «мода» находит употребление в тех случаях, когда определяется наиболее часто встречающееся значение признака, иначе говоря, мода – это варианта (х), у которой частота (вес) наибольшая (наиболее часто встречающееся в совокупности значение признака).

Особенности применения моды:

1. если все значения вариационного ряда имеет одинаковую частоту, то этот вариационный ряд не имеет моды;

2. если две соседних варианты имеют одинаковую доминирующую частоту, то мода вычисляется как среднее арифметическое этих вариант;

3. если две несоседних варианты имеют одинаковую доминирующую частоту, то такой вариационный ряд называется бимодальным;

4. если таких вариант более двух, то ряд полимодальный.

Модальная величина по дискретному ряду находится по наибольшей частоте. Например, по предприятию имеются следующие данные о тарифных разрядах 24 рабочих:

Тарифный разряд	2	3	4	5	6
Число рабочих, чел.	4	5	9	4	2

Как видно из приведенного вариационного ряда, наиболее часто встречающейся величиной, т.е. модой этого ряда, является тарифный разряд 4, который присвоен 9 рабочим из 24.

Несколько сложнее определение моды в интервальном вариационном ряду. В этих случаях необходимо определить модальный интервал (по наибольшей частоте), а конкретное значение моды в интервале вычисляется по формуле:

,

(20)

где – нижняя граница модального интервала (модальный интервал определяется по наибольшей частоте f );

– величина модального интервала;

- частота модального интервала;

- частота предмодального интервала;

- частота послемодального интервала.

Моду можно изобразить графически. Она определяется по гистограмме распределения. Для этого выбирается самый высокий прямоугольник, который является в данном случае модальным. Затем правую вершину модального прямоугольника соединяем с правым верхним углом предыдущего прямоугольника. А левую вершину модального прямоугольника – с левым верхним углом последующего прямоугольника. Далее из точки их пересечения опускают перпендикуляр на ось абсцисс. Абсцисса точки пересечения этих прямых и будет модой распределения.

Медиана – это значение изучаемого признака, приходящееся на середину ранжированной совокупности.

Для определения медианного значения признака в дискретном вариационном ряду находят номер медианной единицы ряда:

,

(21)

где n – объем совокупности.

В данном случае . Полученное дробное значение указывает, что точная середина находится между 95-м и 96-м рабочим. Необходимо определить, к какой группе относятся рабочие с этими порядковыми номерами. Это можно сделать, рассчитав накопленные частоты. Очевидно, что рабочих с этими номерами нет в первой группе, где всего лишь 12 человек, нет их во второй группе (12 + 48). 95-й и 96-й рабочие находятся в третьей группе (12 + 48 + 46), следовательно медианным является 4-й разряд.

В отличие от дискретных вариационных рядов определение медианы по интервальным рядам требует проведения определенных расчетов на основе следующей формулы:

,

(22)

где – нижняя граница медианного интервала;

– величина медианного интервала;

- частота медианного интервала;

- наколенная частота предмедианного интервала.

Для установления медианного интервала необходимо определять накопленную частоту каждого последующего интервала до тех пор, пока она не превысит половины суммы накопленных частот (50%).

Медиану можно изобразить графическим посредством кумуляты. Для ее определения из точки накопленных частот, соответствующей 50%, проводятся прямая, параллельная оси абсцисс, до пересечения с кумулятой. Затем из точки пересечения указанной прямой с кумулятой опускается перпендикуляр на ось абсцисс. Абсцисса точки пересечения является медианой.
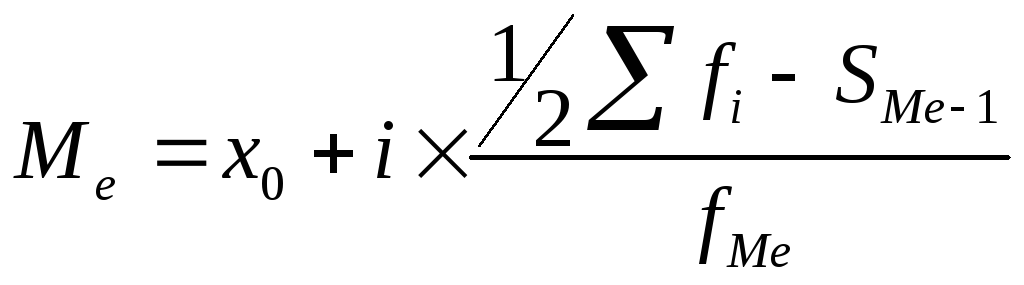