§1.21. Закон сохранения энергии.

Работа и кинетическая энергия. Мощность.

В качестве единой количественной меры различных форм движения материи и соответствующих им взаимодействий в физике вводится скалярная величина, называемая энергией.

Элементарная работа силы .

dA = [Дж]

но

где ds =путь точки за время dt

α – угол между силой и элементарным перемещением .

Сила не совершает работы в двух случаях:

1. точка приложения силы неподвижна ().

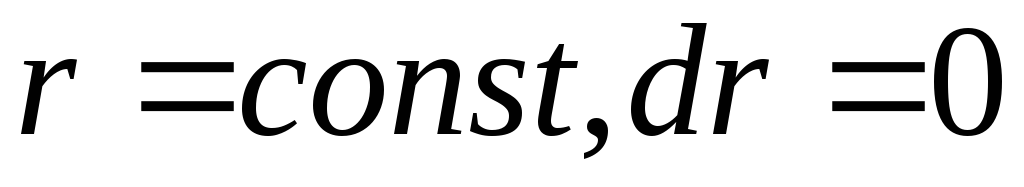1. α = ±π/2, т.е. сила направлена по нормали к траектории и точки её приложения (┴).

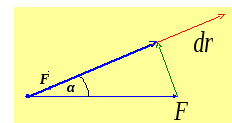
Если α – острый, то dA > 0, такая сила называется движущей силой,

если α – тупой, то dA < 0 и сила называется тормозящей силой.

dA = F_Xdx + F_ydy + F_zdz, откуда А_1,2 = 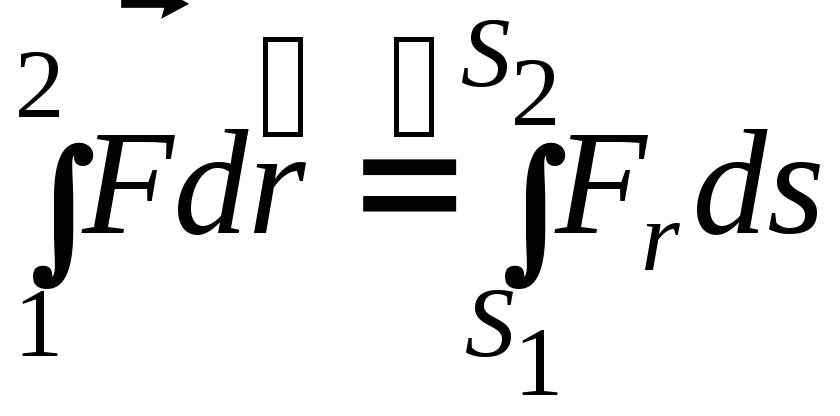, где F_i = cosαS_n ds – дуговая координата точки, отсчитываемая вдоль её траектории.

Сила , действующая на материальную точку, называется потенциальной или консервативной, если работа этой силы не зависит ни от вида траектории точки между её начальным (1) и конечным (2) положениями, ни от закона движения точки по траектории, а зависит только от начального и конечного положения точки.

Работа потенциальной силы на произвольной замкнутой траектории L равна нулю

Примером непотенциальных сил является сила трения.

Мощность N силы N=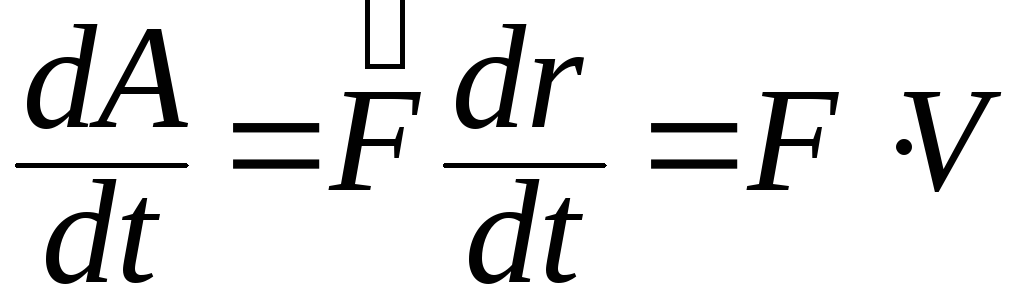 [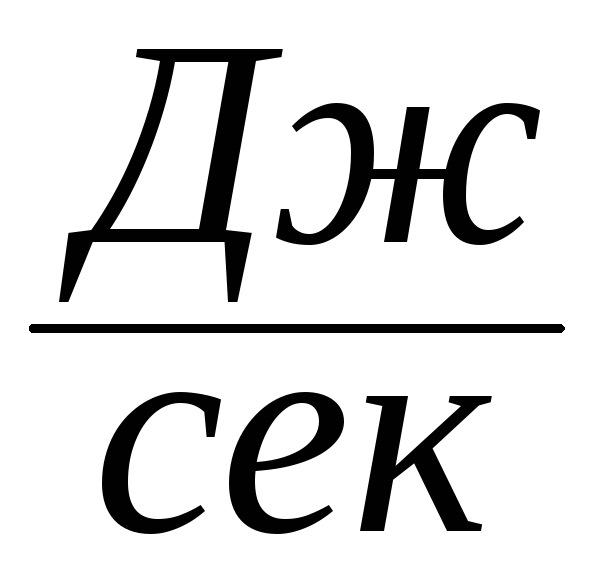] = [вт]

В механике различают два вида механической энергии: кинетическую и потенциальную.

Кинетическая энергия механической системы – энергия механического движения этой системы. Изменение кинетической энергии материальной точки происходит под действием приложенной к ней силы и равно работе, совершаемой этой силой:

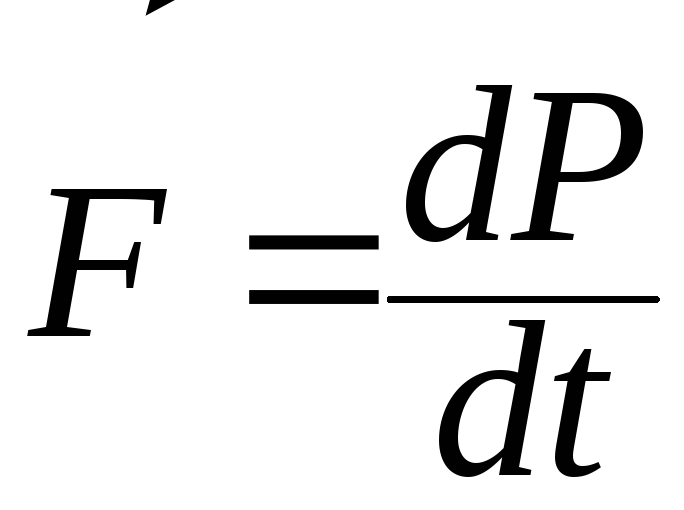dW_k= , но т.к. , то

dW_k=,

где

Т.к. ,

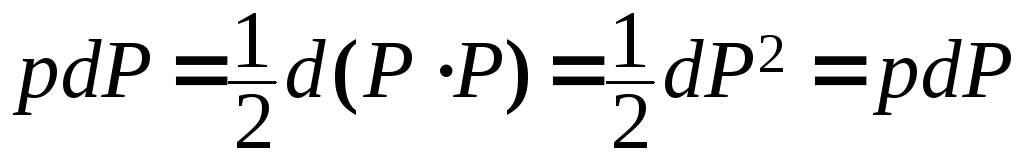то dW_k =

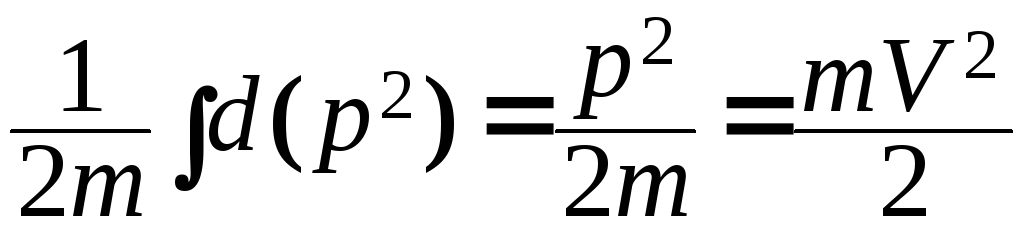
W_k =

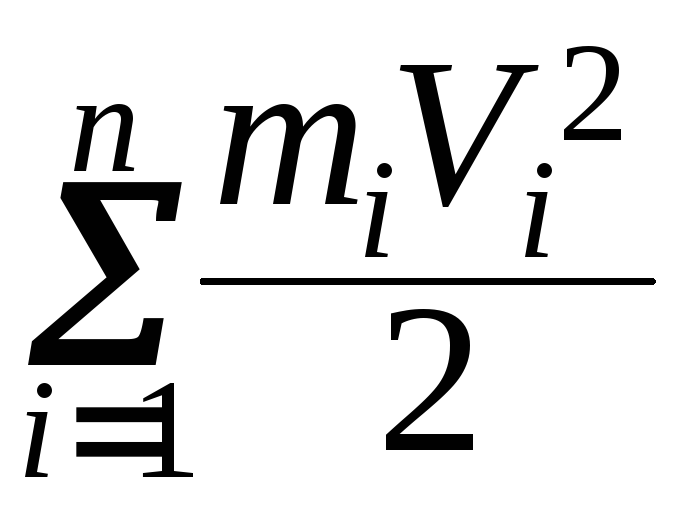
W_k полностью определяется значением масс и скоростей входящих в систему материальных точек. Она не зависит от ,,предыстории” системы. Это важное утверждение формулируется так: кинетическая энергия системы есть функция её механического движения.

В отличие от импульса W_k не зависит от того, в каких направлениях движутся её части.

§1.22. Связь между кинетическими энергиями в различных системах отсчета.

Рассмотрим две системы отсчета: инерциальную систему отсчета k и систему отсчета k'; движущуюся относительно k со скоростью 

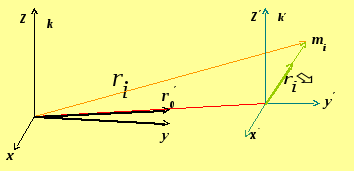
Можно показать, что

W_к =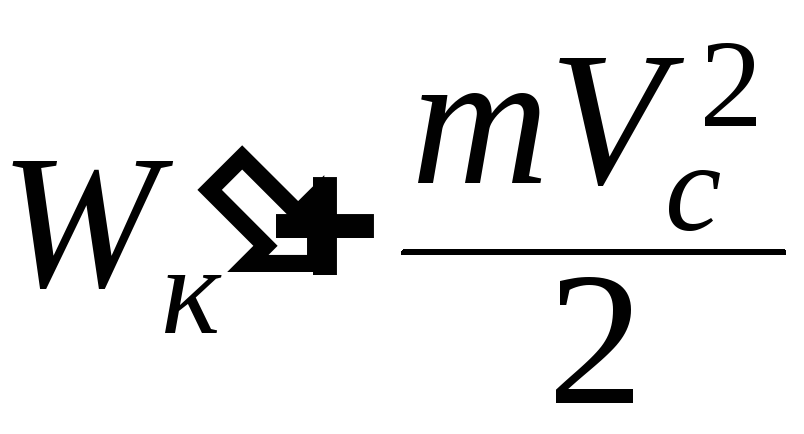- теорема Кёнига.

§1.23. Энергия движения тела как целого.

W_k=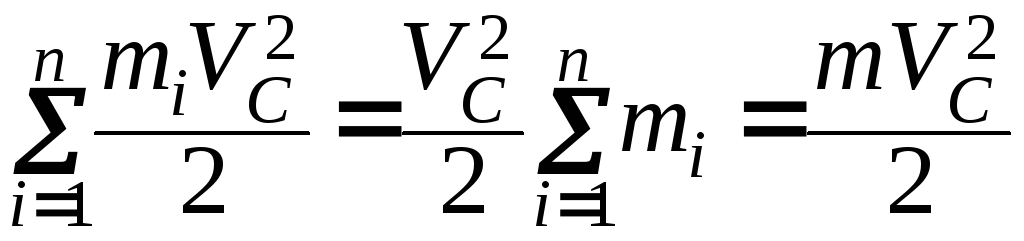

Кинетическая энергия поступательно движущегося тела равна ,

где m – масса тела.

§1.24. Потенциальная энергия.

Работа, совершаемая потенциальными силами при изменении конфигурации системы, т.е. расположения её частей относительно системы отсчета, не зависит от пути перехода из начального состояния в конечное. Работа эта А_1-2 полностью определяется начальной и конечной конфигурациями системы. Следовательно, её можно представить в виде разности значений некоторой функции конфигурации системы W_n , называемой потенциальной энергией системы

A_1-2=W_n(1) – W_п(2) или dA = - dW_п

dA = - dW_n

но dA= откуда

dA=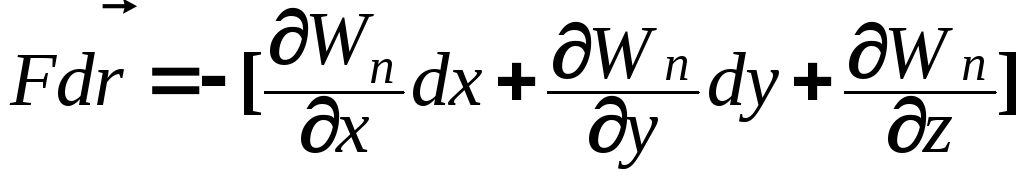

Откуда

F_x= –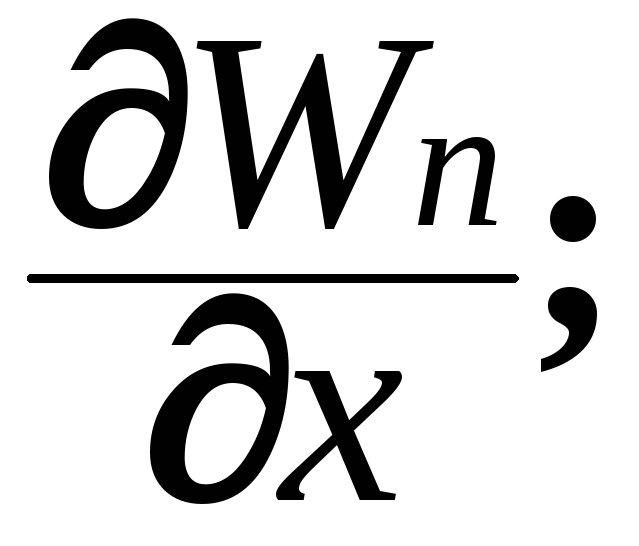 F_y= – F_z= –

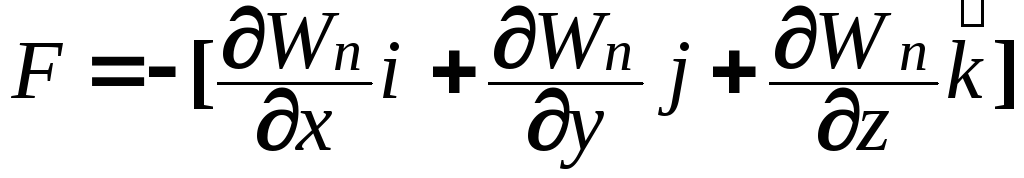
или коротко

- оператор набла.

Пример:

Потенциальная энергия материальной точки в однородном поле.

Поле однородно (силовое поле), если сила , одинакова во всех точках поля. Если сила направлена вдоль оси z, то .

dW_п = - dA = - F_zdz

W_п(z) – W_п(0) = -

или W_п(z) = - F_z∙z + W_п(0)

Например, тело массы m в однородном поле силы тяжести

F_z = mg (ось z направлена вверх)

W_п = mgh где h – высота подъёма над поверхностью Земли, а на поверхности Земли W_п= 0