§2.20. Теплоёмкость многоатомных газов.

Удельная теплоёмкость

(единица массы вещества)

Молярная теплоёмкость –

(1моль вещества)

Различают теплоёмкости при постоянном объёме и постоянном давлении, если в процессе нагревания вещества его объём или давление остаётся постоянным. Для одного моля газа

Из первого начала Т.Д. имеем:

C_m · dT =dU_m + РdV_m

при V = const → C_m dT = C_V · dT = dU_m

.

Для произвольной массы газа

,

следовательно

при P = const

откуда

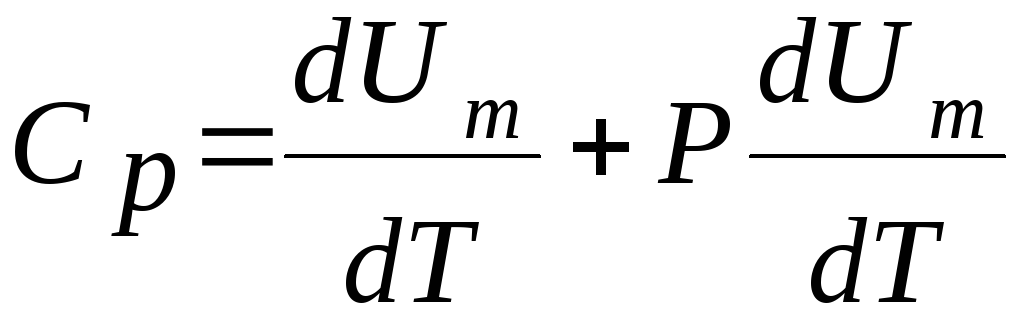но

.

Из уравнения Менделеева-Клапейрона

откуда

C_P = C_V + R – уравнение Майера.

но т.к. 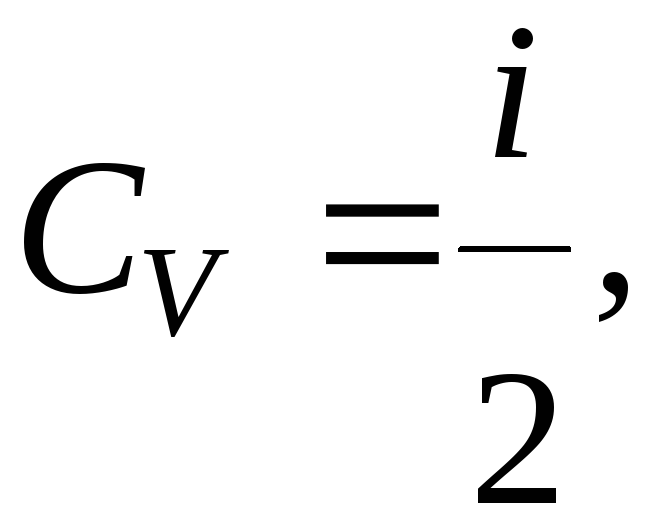то

коэффициент Пуассона.

С_P и С_V не зависят от температуры, а определяются лишь числом степеней свободы. Это утверждение МКТ справедливо в довольно широком интервале температур лишь для одноатомных газов.

Уже для двухатомных газов число степеней свободы зависит от температуры.

Для двухатомной молекулы есть три поступательных, две вращательных и одна колебательная степень свободы (на колебательную степень свободы приходится 2 степени свободы – потенциальная и кинетическая энергии).

По закону равномерного распределения энергии по степеням свободы для комнатных температур Эксперимент даёт для молекулы водорода Н₂ следующую зависимость

При низких температурах наблюдается только поступательное движение (колебательные и вращательные степени свободы ,,выморожены”) при более высоких температурах добавляется вращение, а при высоких ещё и колебания молекул.

Расхождение теории и эксперимента объясняется квантованием колебательной и вращательной энергии. Если энергия теплового движения недостаточна для возбуждения колебаний, то эти колебания не вносят вклада в теплоёмкость, соответствующая степень свободы ,,замораживается” и к ней неприменим закон о распределении энергии. Аналогично можно объяснить уменьшение теплоёмкости при низкой температуре - ,,замораживается” вращательные степени свободы.

В этом – недостатки классической теории теплоёмкости.

§2.21. Применение первого начала термодинамики

к изопроцессам и к адиабатическому процессу.

1. Изохорный процесс (V = const).

dQ = dU но dU_m = C_VdT

тогда для произвольной массы газа

2) Изобарный процесс (P = const).

из основного уравнения МКT

откуда dQ = dU + P∆V

3. Изотермический процесс (T = const).

dT = 0→

=

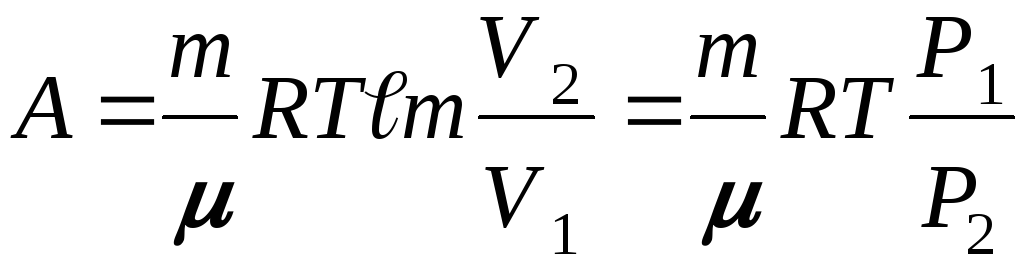
т.е. при T = const

или

3. Адиабатический процесс (δQ = 0).

δА = -dU

т.к. δА = - dU, а или

имеем

из основного уравнения МКТ

имеем

разделив (2) на (1) имеем

но

откуда

интегрируя получаем

уравнение адиабаты (уравнение Пуассона).

Используя уравнение Менделеева-Клайперона из уравнения Пуассона можно также получить:

§2.22. Работа в адиабатическом процессе.

где

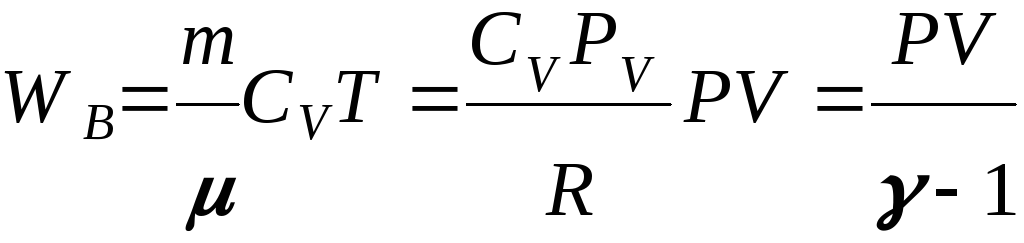
PV^γ = const

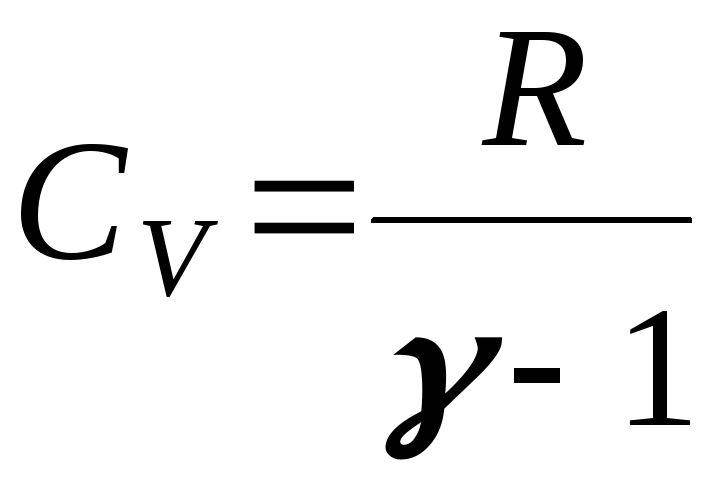
C_V= dU

i(γ -1)

T₂V₂^γ-1 = T₁V₁

TV^γ-1 = const

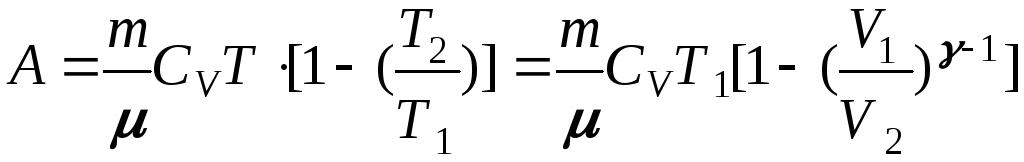
учитывая, что можно получить

TV^γ-1 = const

T^γ P^1-γ = const γ – показатель адиабаты.

Работа в адиабатическом процессе будет

Это выражение можно преобразовать к виду