§2.3. Уравнение состояния идеального газа.

Уравнение состояния – устанавливает связь между параметрами состояния. В простейшем случае равновесное состояние тела определяется P, V, T. Связь между ними аналитически можно выразить так:

F(P, V, T) = 0

где F – некоторая функция параметров.

Это - уравнение состояния газа.

При обычных условиях параметры состояния многих газов хорошо описываются уравнением

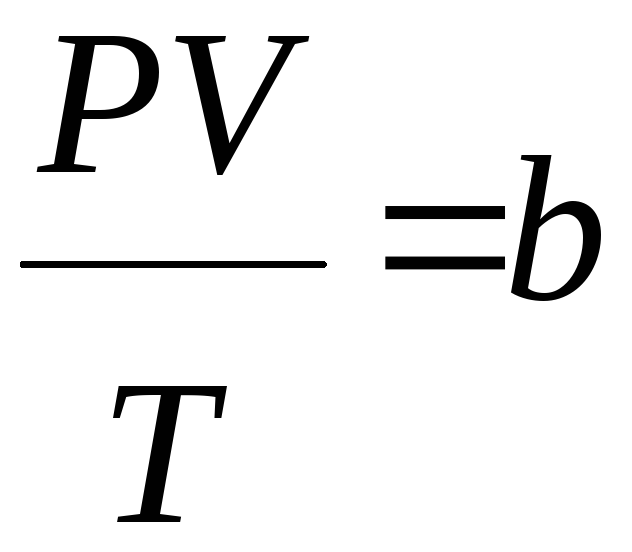
где b – константа, пропорциональная массе газа.

Это уравнение выполняется точно для идеального газа.

Идеальный газ – газ, молекулы которого не взаимодействуют друг с другом и имеют пренебрежимо малый объём. Молекулы соударяются друг с другом абсолютно упруго.

Если ввести молярный объём 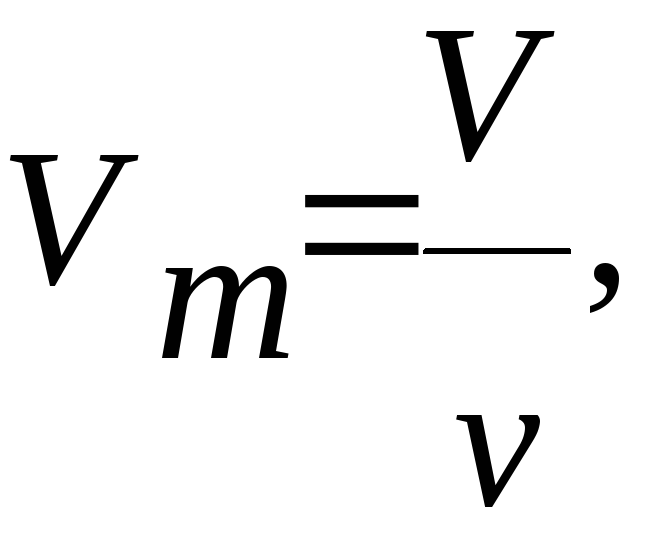где ν – количество вещества и учесть , что

m = m₀N_Aν =µν

где m₀ – масса одной молекулы.

µ - молекулярная масса.

N_A – число Авогадро,

то уравнение состояния можно записать в виде

р V_m ν = b · T или PV_m = RT *

Согласно закону Авогадро при одинаковых давлениях и температурах молярные объёмы V_m различных газов одинаковы.(V_m = 22.4·10^-3м³) при Н.У.

Из этого закона и уравнения * следует, что постоянная R одинакова для всех газов. Это - универсальная газовая постоянная R = 8.31 Дж/(моль۰К)

Для произвольной массы газа

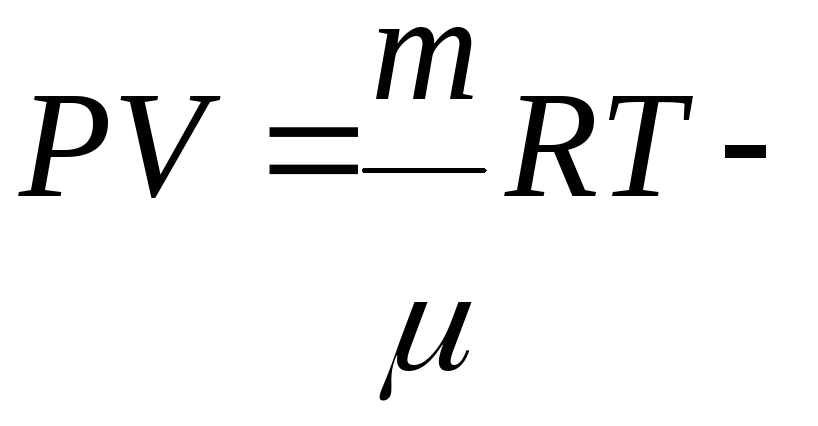* *уравнение Менделеева Клапейрона,

т.к. R = kN_A , где k – постоянная Больцмана

k = 1.38 · 10^-23 Дж/К из ** получаем

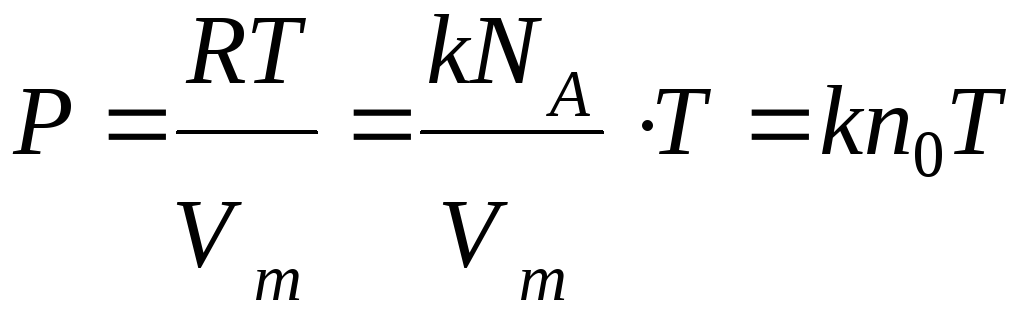
Р = kn₀T

§2.4. Давление газа с точки зрения молекулярно-кинетической теории.

При своём движении молекулы газа ударяются о стенку сосуда, создавая тем самым давление.

Если газ находится в равновесии все направления движения молекул равновероятны. Если n₀ – концентрация молекул (число молекул в единице объёма)

то в данном направлении движется число молекул равное

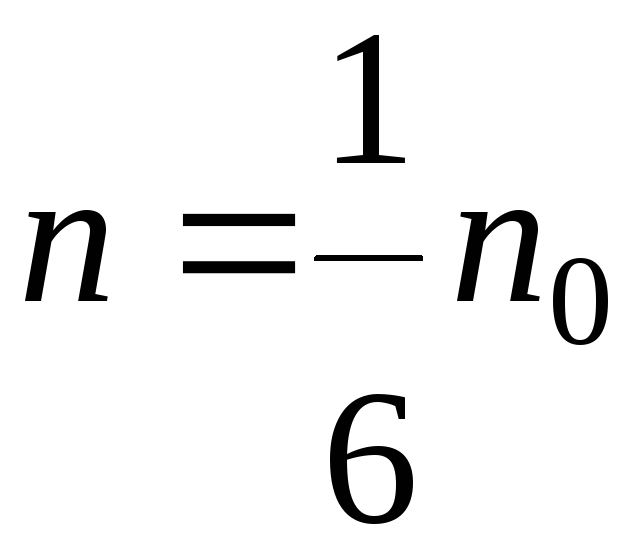(в единице объёма).

N = nVdt·S– число молекул, ударяющихся упруго о стенку за время dt. При этом

dP = 2m₀V·N где m₀ – масса одной молекулы и

.

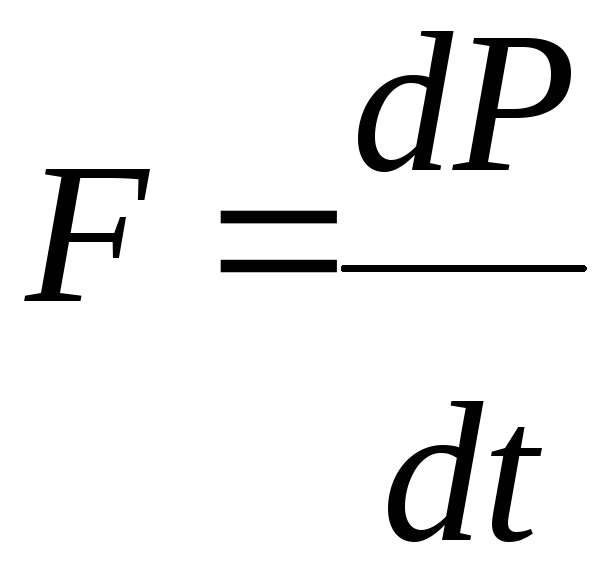Следовательно

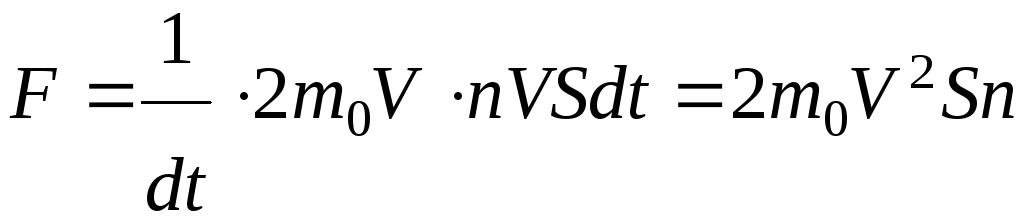
Откуда давление

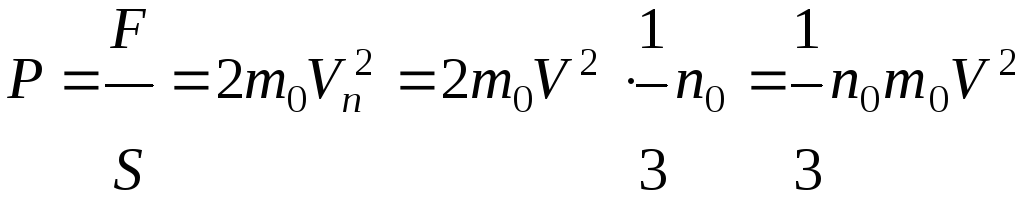
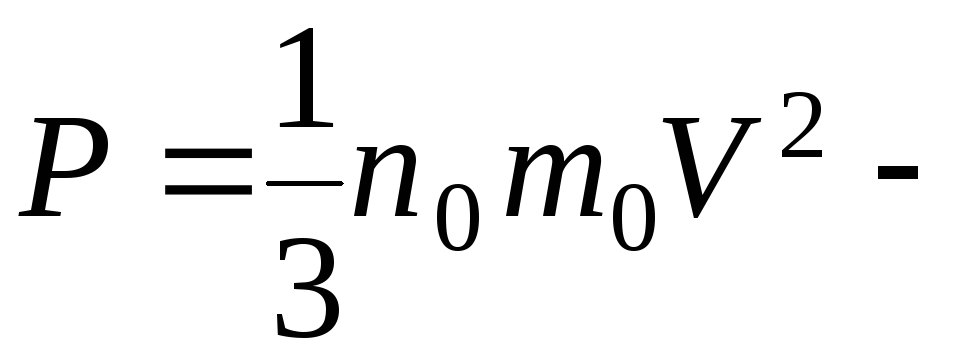основное уравнение молекулярно-кинетической теории.

§2.5. Молекулярно-кинетический смысл температуры.

Сравнивая уравнения

P = n₀ kT

и

,

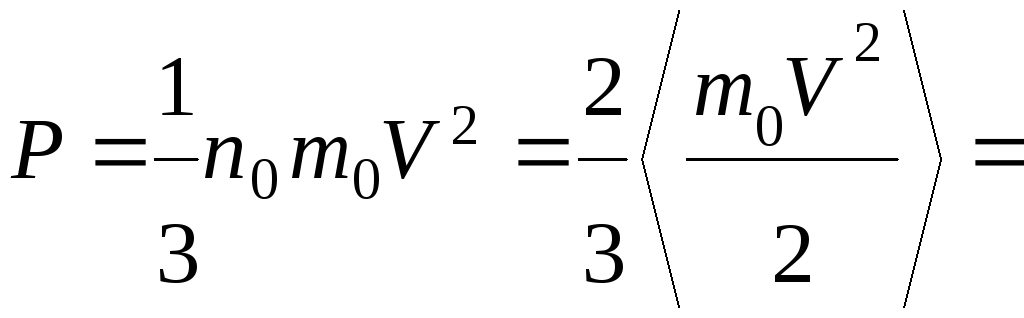
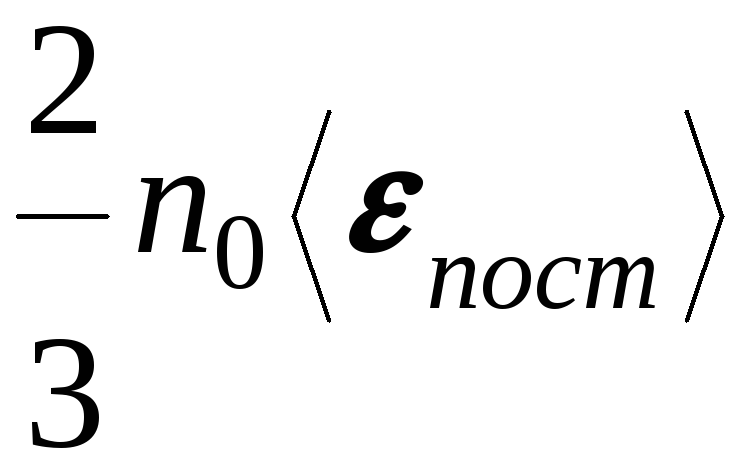где средняя кинетическая энергия поступательного движения. Имеем

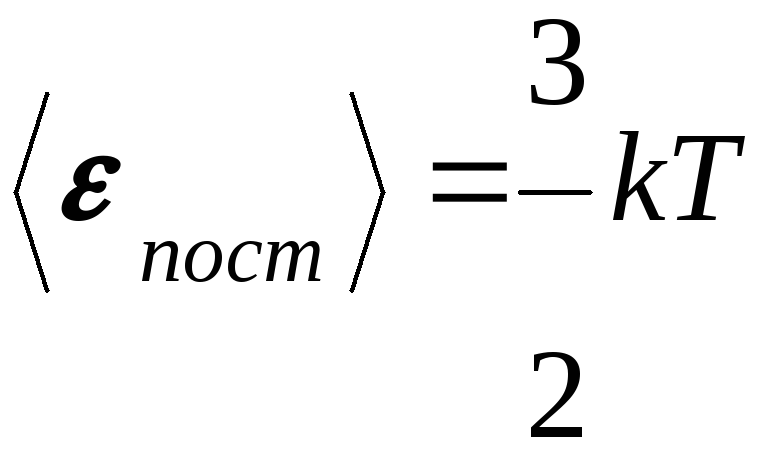
Термодинамическая температура есть мера кинетической энергии молекул.

Средняя энергия молекул зависит только от температуры и не зависит от массы молекул.

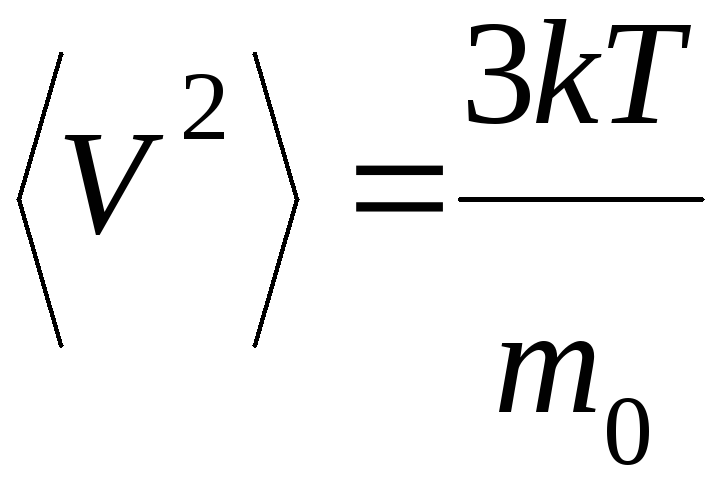
среднеквадратичная скорость молекул.

Многоатомные молекулы кроме поступательного могут совершать также вращательное и колебательное движения. Эти виды движения связаны с запасом энергии, вычислить который позволяет устанавливаемый классической статистической физикой закон равнораспределения энергии по степеням свободы молекулы.

Числом степеней свободы механической системы называется количество независимых координат, с помощью которых может быть задано положение системы в пространстве.

Система из N материальных точек, между которыми нет жестких связей, имеет 3N, степеней свободы (положение каждой точки определяется тремя координатами x, y, z). Каждая жёсткая связь уменьшает число степеней свободы на единицу.

На каждую степень свободы (поступательную, вращательную и колебательную), в среднем, приходится энергия, равная .

Поэтому средняя энергия молекулы

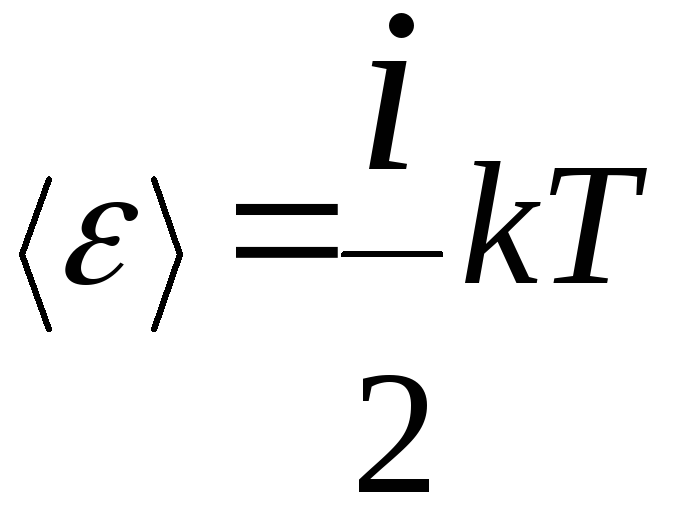
где i – сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекулы

i = i_пост + i_вращ + 2i_колеб

(2i_колеб, т.к. i_колеб на потенциальную энергию и i_пост на кинетическую энергию).

Закон равнораспределения получен на основе классических представлений о характере движения молекул. Поэтому он является приближенным и нарушается в тех случаях, когда становятся существенными квантовые эффекты.

Резюме

• 

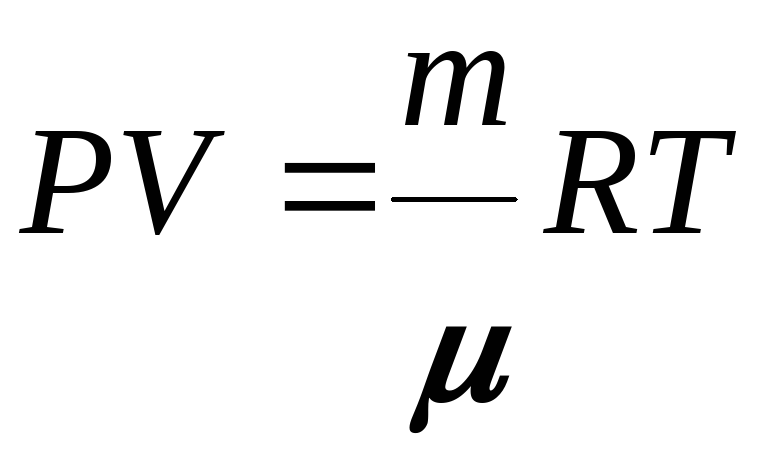
• P = n₀ kT

• ,

• 

• 

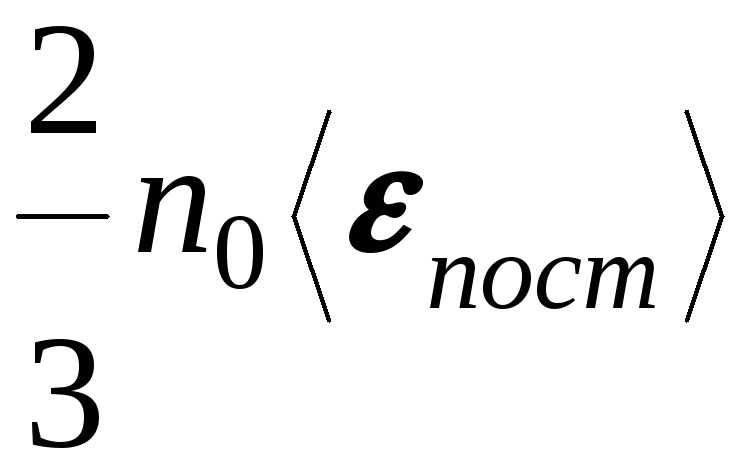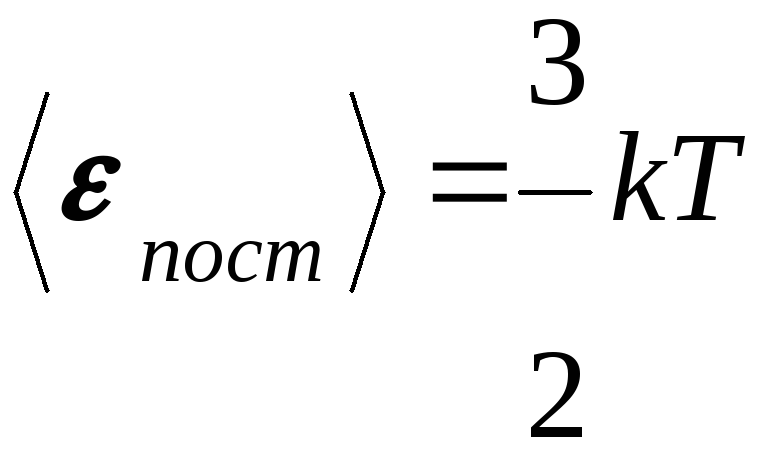
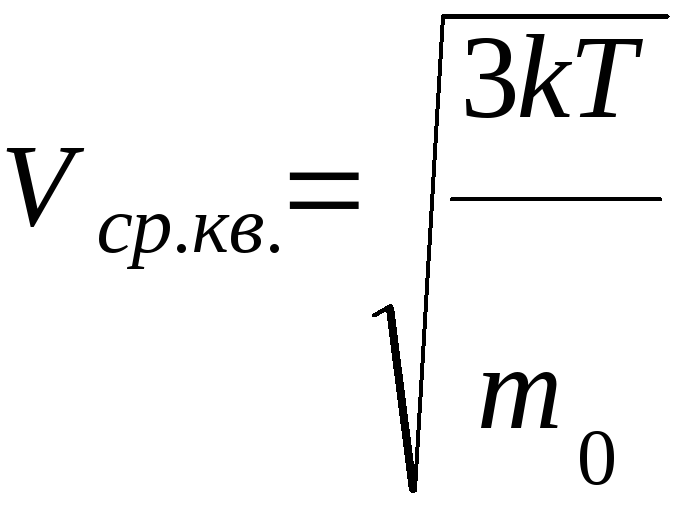
Л-11