§2.26. Свойства энтропии.

1. Энтропия – функция состояния. Если процесс проводят вдоль адиабаты, то энтропия системы не меняется. Значит адиабаты – это одновременно и изоэнтропы. Каждой более ,,высоко” расположенной адиабате отвечает большое значение энтропии.

2. Энтропия – величина аддиативная: энтропия макросистемы равна сумме энтропий ее отдельных частей.

3. Одно из важнейших свойств энтропии заключается в том, что энтропия замкнутой (т.е. теплоизолированной) макросистемы не уменьшается – она либо возрастает, либо остается постоянной.

Принцип возрастания энтропии замкнутых систем представляет собой еще одну формулировку второго начала термодинамики.

Величина возрастания энтропии в замкнутой макросистеме может служить мерой обратимости процессов, протекающих в системе.

Пример.

Идеальный газ, находящийся в некотором состоянии, адиабатически (т.е. без теплообмена) расширили до объема Одинаково ли будет установившееся давление газа в конечном состоянии (в объеме ), если процесс расширения

обратимый,

необратимый

В соответствии с принципом возрастания энтропии в замкнутой системе при необратимом процессе энтропия должна увеличиваться. Значит установившееся состояние будет соответствовать точке на более высокой адиабате, т.е. давление будет больше.

Теорема Нернста (1906). Это теорема утверждает, что при приближении температуры к абсолютному нулю энтропия макросистемы также стремится к нулю:

при

и мы можем вычислять абсолютное значение энтропия по формуле

§2.27. Вычисление и применение энтропии.

1. Основное уравнение термодинамики. Оно представляет собой объединение энтропии с первым началом. . Для обратимых процессов:

Это уравнение имеет многочисленные применения.

2. Энтропия идеального газа. Пусть начальное и конечное состояния, 1 и 2, газа определяются параметрами и

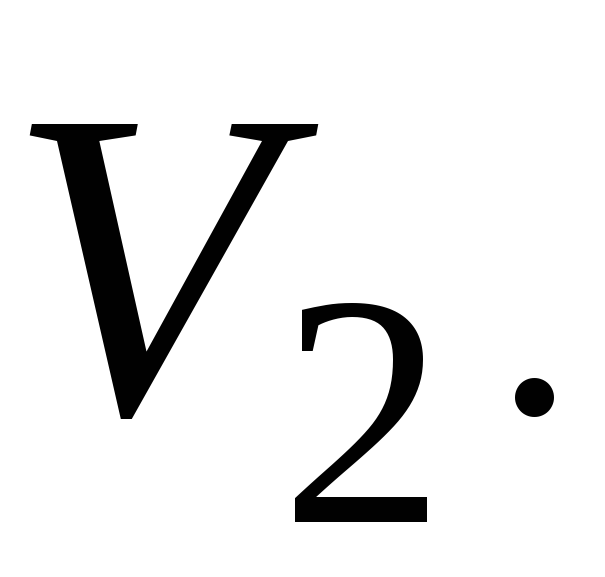
Элементарное приращение энтропии газа с учетом, что и определяется как

Взяв дифференциал логарифма от получим

формуле можно придать симметричный вид:

где учтено, что

Проинтегрировав последнее выражение получим в результате

3. Приращение энтропии при необратимом процессе между двумя равновесными состояниями 1 и 2. Приращение энтропии по обратимому изотермическому процессу:

> 0.

4. Возрастание энтропии при смешении газов. Пусть в двух половинах теплоизолированного сосуда объемом находятся два идеального газа, 1 и 2, разделенных перегородкой. Температура, давление и число молей и обеих половинах одинаково. После удаления перегородки начинается необратимый процесс смешения газов. В конце концов он прекращается, и система приходит в равновесное состояние, в котором оба газа равномерно перемешаны. Температура в конечном состоянии будет такая же, так как система теплоизолирована и газы идеальные. Используя результат предыдущего примера, находим, что при приращение энтропии каждого газа т.е. суммарное приращение энтропии системы

Приращение ∆S > 0, что естественно, поскольку процесс смещения существенно необратимый (обратимый процесс – самораспределение смеси двух газов – совершенно невероятен). Последняя формула приводит к выводу, называемому парадоксом Гиббса. Формула справедлива только при смешивании различных газов.