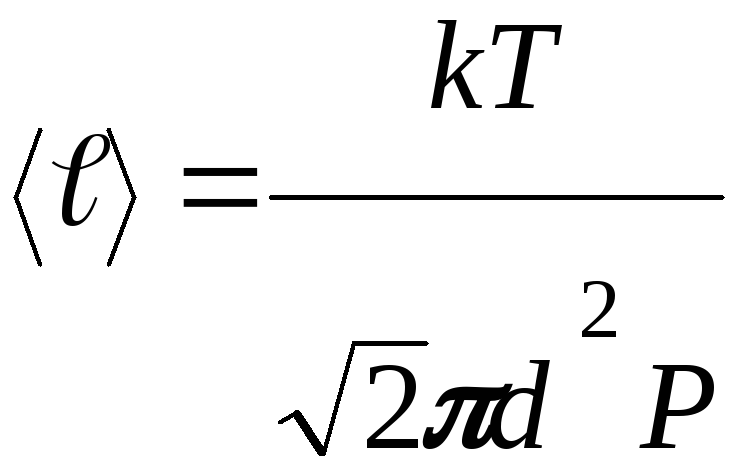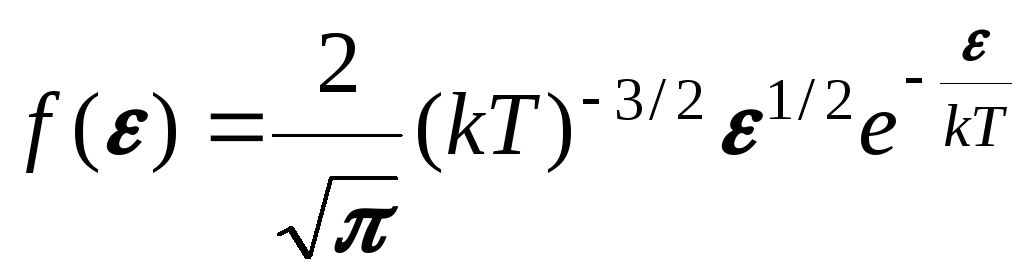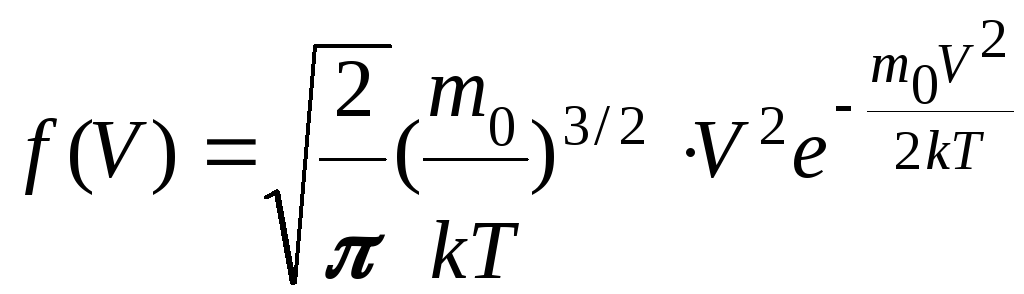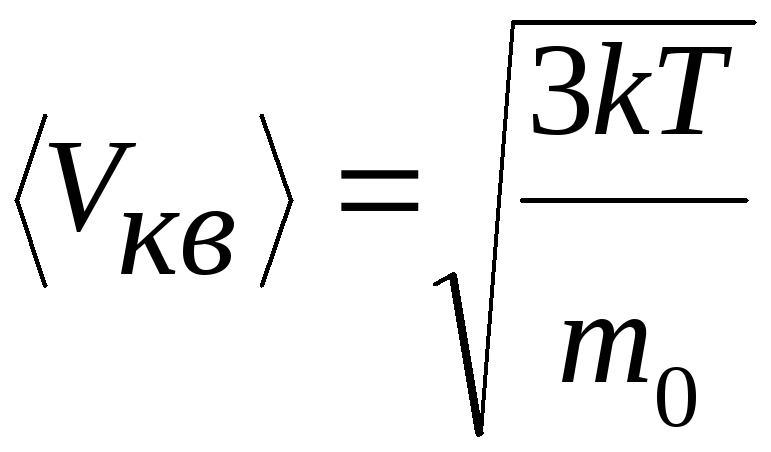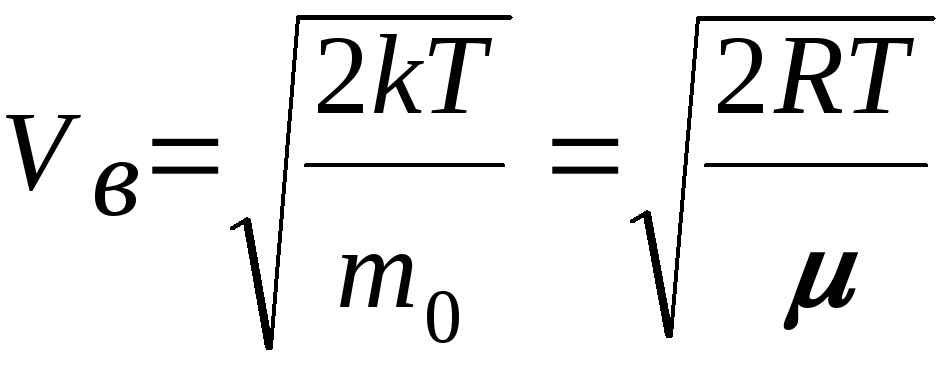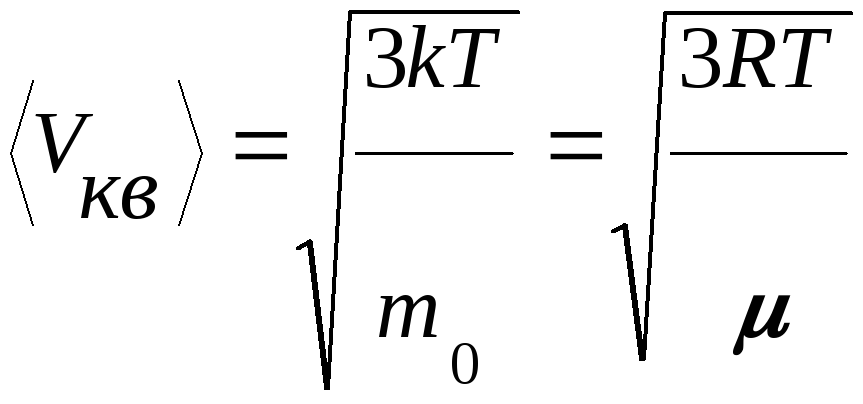- •Глава I. Физические основы динамики.
- •§1.1. Предмет механики. Кинематика и динамика. Классическая механика. Квантовая механика. Релятивистская механика.
- •§1.2. Силы.
- •§1.3. Элементы кинематики.
- •§1.4. Пространство и время.
- •§1.5. Кинематическое описание движения.
- •§1.6. Вектор перемещения. Скорость. Ускорение.
- •§1.7. Движение точки по окружности.
- •§1.8. Линейная скорость точки.
- •§1.9. Связь между угловыми и линейными параметрами движения.
- •Решение:
- •§1.10. Элементы динамики поступательного движения. Основная задача динамики. Понятие состояния в классической механике. Масса, импульс, сила.
- •§1.11. Современная трактовка законов Ньютона.
- •§1.12. Второй закон Ньютона как уравнение движения импульса.
- •§1.13. Третий закон Ньютона.
- •§1.14. Закон сохранения импульса.
- •§1.15. Реактивное движение. Уравнение Мещерского.
- •Решение
- •Решение
- •§1.16. Преобразование скорости и ускорения
- •§1.17. Неинерциальные системы отсчета. Силы инерции.
- •§1.18. Силы инерции.
- •§1.19. Особенности сил инерции.
- •§1.20. Принцип эквивалентности.
- •§1.21. Закон сохранения энергии.
- •§1.22. Связь между кинетическими энергиями в различных системах отсчета.
- •§1.23. Энергия движения тела как целого.
- •§1.24. Потенциальная энергия.
- •§1.25. Законы сохранения и симметрия пространства.
- •§1.26. Графическое представление энергии.
- •§1.27. Элементы механики твердого тела.
- •§1.28. Момент инерции диска. Теорема Штейнера
- •§1.29. Момент силы
- •§1.30. Работа при вращательном движении.
- •§1.31. Момент импульса. Закон сохранения момента импульса.
- •§1.32. Условия равновесия твердого тела.
- •§1.33. Принцип относительности в механике. Инерциальные системы отсчёта и принцип относительности. Преобразования Галилея.
- •§1.34. Постулаты специальной теории относительности.
- •§1.35. Следствия из преобразований Лоренца.
- •§1.36. Элементы релятивистской динамики.
- •§1.37. Работа и энергия. Законы сохранения энергии и импульса.
- •§1.38. Механика колебаний и волн.
- •§1.39. Векторные диаграммы.
- •§1.40. Комплексная форма представления колебаний
- •§1.41. Сложение гармонических колебаний.
- •§1.42. Биения
- •§1.43. Кинетическая и потенциальная энергия при гармонических механических колебаниях.
- •§1.44. Гармонический осциллятор.
- •§1.45.Свободные и затухающие колебания.
- •§1.46. Вынужденные колебания осциллятора под действием синусоидальной силы.
- •§1.47. Волновые процессы.
- •§1.48. Эффект Доплера.
- •§1.49. Групповая скорость и её связь
- •§1.50. Одномерное волновое уравнение.
- •Глава II. Статистическая физика и термодинамика.
- •§2.1. Динамические и статистические закономерности в физике. Статистический и термодинамический методы.
- •§2.2. Макроскопические состояния.
- •§2.3. Уравнение состояния идеального газа.
- •§2.4. Давление газа с точки зрения молекулярно-кинетической теории.
- •§2.5. Молекулярно-кинетический смысл температуры.
- •§2.6. Статистические распределения.
- •§2.7.Скорости теплового движения частиц. Распределение частиц по абсолютным значениям скорости.
- •§2.8.Средняя кинетическая энергия частицы.
- •§2.9.Распределение Больцмана.
- •§2.10. Явления переноса. Понятие о физической кинетике.
- •§2.11. Эффективное сечение. Длина свободного пробега.
- •§2.12. Явления переноса.
- •§2.13. Теплопроводность.
- •§2.14. Диффузия.
- •§2.15. Внутреннее трение (вязкость).
- •§2.16. Основы термодинамики.
- •§2.17. Работа газа при изменении
- •§2.18. Эквивалентность теплоты и работы.
- •§2.19. Первое начало термодинамики.
- •§2.20. Теплоёмкость многоатомных газов.
- •§2.21. Применение первого начала термодинамики
- •§2.22. Работа в адиабатическом процессе.
- •§2.23. Энтропия.
- •§2.24. Изменение энтропии в изопроцессах.
- •4) Адиабатный.
- •§2.25. Связь энтропии с вероятностью состояния системы. Принцип возрастания энтропии.
- •§2.26. Свойства энтропии.
- •§2.27. Вычисление и применение энтропии.
- •§2.28. Цикл Карно.
- •§2.29. Второе начало термодинамики.
- •По Кельвину:
- •По Клаузиусу:
- •§2.30. Цикл Карно. Максимальный кпд тепловой машины.
- •§2.31. Фазовые равновесия и фазовые превращения. Фазы и фазовые превращения.
- •§2.32. Фазовые переходы I рода.
- •§2.33. Фазовые переходы II рода
- •§2.34. Условия равновесия фаз. Фазовые диаграммы.
- •§2.35. Метастабильные состояния.
- •§2.36. Реальные газы. Уравнение Ван-дер-Ваальса.
- •1) Учёт собственного объёма молекул.
- •2) Учёт притяжения молекул.
- •V метастабильные состояния Резюме
- •Оглавление
- •1.1. Элементы кинематики
- •1.2. Элементы динамики частиц
- •1.3. Законы сохранения импульса и механической энергии
- •1.4. Элементы механики твердого тела
- •1.5. Принцип относительности Галилея
- •1.6. Элементы релятивистской динамики
- •2. Механика колебаний и волн
- •2.1. Кинематика гармонических колебаний
- •2.2. Гармонический осциллятор
- •2.3. Волновые процессы
- •3. Статистическая физика и термодинамика
- •3.5. Реальные газы, жидкости и кристаллы
§2.8.Средняя кинетическая энергия частицы.
Исходя из распределения молекул по скоростям

можно найти распределение молекул газа по значениям кинетической энергии ε.
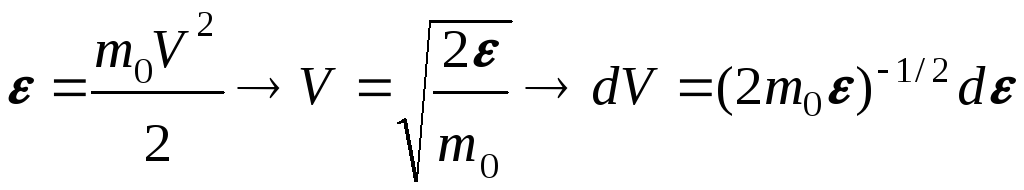
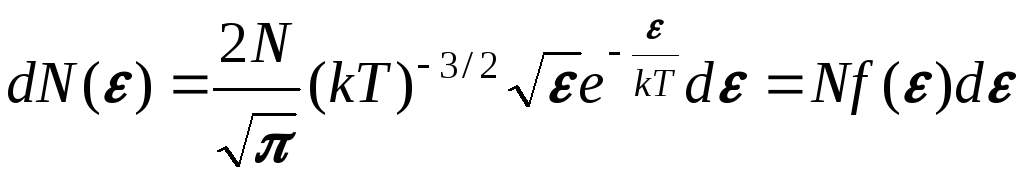
откуда

Средняя кинетическая
энергия молекулы
![]() идеального газа
идеального газа
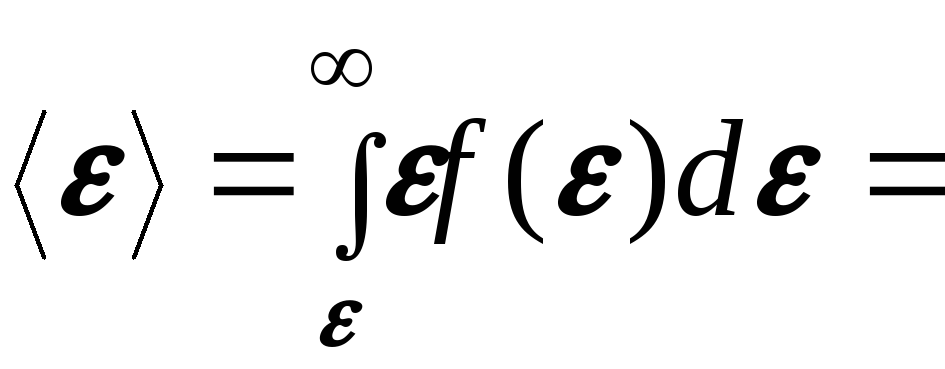

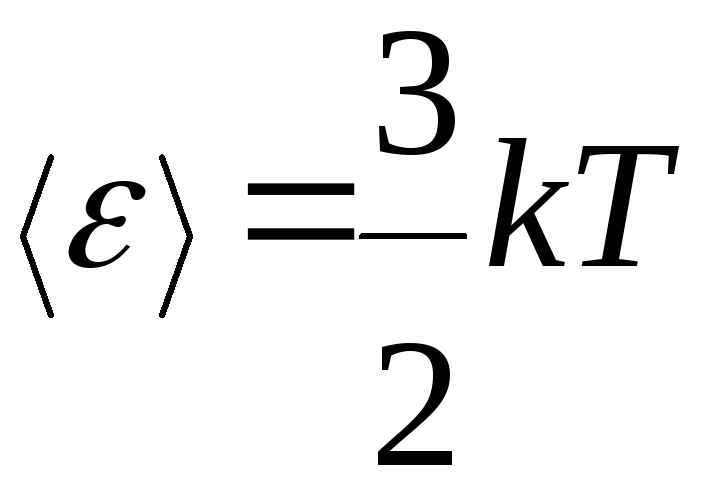
§2.9.Распределение Больцмана.
Если молекулы находятся в силовом поле (например, поле силы тяжести), то давление газа будет меняться с высотой: Если ρ = const, то Р = ρgh.
dP = - ρgdh (минус, т.к. с увеличением высоты давление падает).


или
![]()

Интегрируя, получаем
![]()
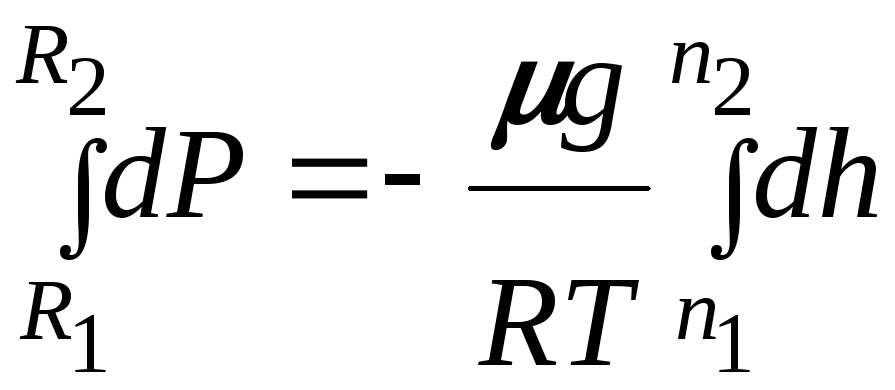
или
![]() барометрическая
формула.
барометрическая
формула.
или если h1 = 0, h2 = h, то
![]() ,
,
где Р – давление на высоте h,
но P = nkT и P0 = n0kТ, где n и n0 ,соответственно, концентрации молекул на высоте h и h = 0, то
![]()
![]() но R
= kNa,
но R
= kNa,
а
 масса
одной молекулы.
масса
одной молекулы.
Следовательно
![]() ,
,
но m0gh = Wпот – потенциальная энергия молекулы в поле силы тяжести, поэтому
![]()
Распределение частиц во внешнем потенциальном поле.
Резюме
Л-12
§2.10. Явления переноса. Понятие о физической кинетике.
Время релаксации.
Физическая кинетика – микроскопическая теория процессов в статистически неравновесных системах. Изучает методами квантовой или классической статистической физики процессы переноса энергии, импульса и вещества в различных физических системах (газах, жидкостях, твердых телах, плазме), а также влияние на эти системы внешних полей.
Физическая кинетика включает в себя, в частности, кинетическую теорию газов.
Кинетическая теория газов основана на следующих общих положениях классической физики:
-
в системе частиц выполняются законы сохранения энергии, электрического заряда и числа частиц;
-
все частицы системы являются ,,мечеными”, т.е. есть возможность отличить тождественные частицы друг от друга;
-
все физические процессы в системе протекают в пространстве времени и непрерывного (т.е. не квантуются);
-
каждая частица системы может иметь совершенно произвольные значения координат и компонент скорости совершенно независимо от значений этих параметров у других частиц системы.
Явления переноса хорошо описываются кинетической теорией газов.
Время, за которое первоначальное отклонение какой-либо величины от равновесного значения уменьшается в e раз, называется временем релаксации. Для каждого параметра состояния имеется своё время релаксации. Наибольшее из этих времён представляет собой время релаксации системы.
§2.11. Эффективное сечение. Длина свободного пробега.
Между двумя
последовательными столкновениями
молекулы проходят некоторый путь ℓ,
который называется длиной свободного
пробега. Средняя длина свободного
пробега –
![]()
Эффективный диаметр молекулы d – минимальное расстояние, на которое сближаются при столкновении центры двух молекул. Он зависит от скорости сталкивающихся молекул, т.е. от температуры (незначительно уменьшается с ростом температуры).
За 1с молекула
проходит путь, равный средней арифметической
скорости
![]() Если
Если
![]() среднее
число столкновений, то
среднее
число столкновений, то

![]()
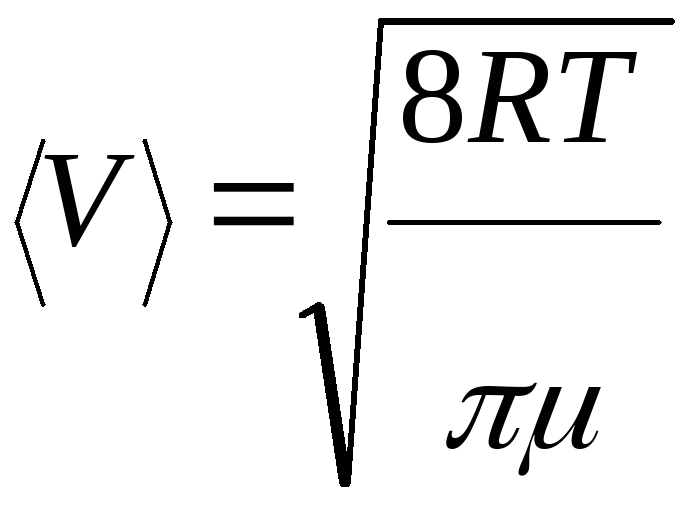
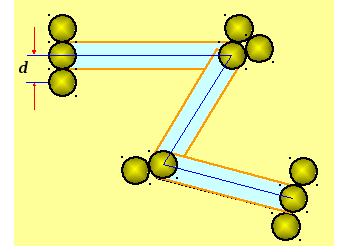
Молекула столкнётся только с теми ,,застывшими” молекулами, центры которых находятся на расстоянии не большем d, т.е. лежат внутри ломаного цилиндра радиусом d. Среднее число столкновений за 1с равно числу молекул в объёме ломаного цилиндра:
![]() ,
,
где n
– концентрация молекул.
![]() объём
цилиндра.
объём
цилиндра.
Откуда
![]()
Если учесть движение других молекул (т.е. не рассматривать их «замороженными»), то
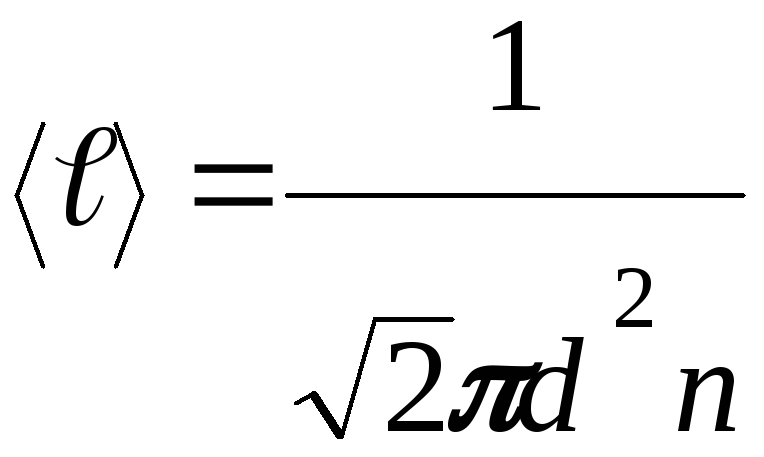
но т.к. P = nkT где P – давления, то