3.3.2. Повышение порядка точности аппроксимации дифференциальных уравнений гиперболического типа
Теперь применим приведенную выше методику повышения порядка точности аппроксимации обыкновенных дифференциальных уравнений к простейшему гиперболическому уравнению. Для случая скорости V0 = const уравнение непрерывности для частиц имеет вид:
;
N(x,
0) = 1027;
N(0,
t)
=
1.2 1027.
(3.3.6)
Алгоритм численного решения уравнения (3.3.6) на разностной сетке заключается в следующем. На первом полушаге τ / 2 алгоритм будем строить на основе схем бегущего счета (см. рис. 3.24, шаблоны выделены жирными линиями).
Гиперболическое уравнение (3.3.6) аппроксимируем следующей системой разностных уравнений:
или
,
(3.3.7)
где χ =
;
i
= 1, 2, …, n;
j
= 0, 1, …k-1.
t
t
tk
j
= k
tk j
= k
j+1
Nij+1
j+1
Nij+1
X=L1
j
Nij
j
Nij
j=0
j=0
0 i-1 i i+1 n х 0 i-1 i i+1 n х
Рис. 3.24. Разностные сетки, используемые на первом и втором полушаге τ / 2 для численного интегрирования гиперболического уравнения (3.3.6)
Гиперболическое уравнение (3.3.6) аппроксимируем следующей системой разностных уравнений:
или
,
(3.3.8)
где
χ
=
;
i
= 1, 2, …, n;
j
= 0, 1, …k-1.
На втором полушаге τ / 2 для гиперболического уравнения (3.3.6), как и в случае с обыкновенным дифференциальным уравнением, построим разностную схему, аппроксимирующую исходное уравнение со вторым порядком точности
(рис. 3.24):
или
,
(3.3.9)
где
χ
=
;
i = 1, 2, …, n; j = 0, 1, …k-1, [III, 10-11].
Результаты численных расчетов функции N(х, t) представлены на рис. 3.25, где сплошной кривой отмечено решение дифференциального уравнения (3.3.6), полученное на основе разностных схем, имеющих второй порядок точности, а пунктирной - первый порядок точности.
Текст программы алгоритма решения гиперболического дифференциального уравнения (3.3.6), написанной на блочно-структурном языке системы MATH CAD и числовые данные, приведены ниже.
На рис. 3.25 представлены результаты численного решения гиперболического уравнения (3.3.6) со вторым порядком точности - сплошная линия и с первым – пунктирная кривая. Максимальное расхождение значений функции N(t) при временном шаге τ = 120 с, полученных на основе двух разностных схем, составляет порядка десятой доли процентов (рис. 3.26) и, соответственно, при таких шагах τ могут использоваться разностные схемы, имеющие первый порядок точности.
Рис. 3.26. Пространственное и временное распределение функции N(х, t)
для τ=120 с
Теперь рассмотрим эти же распределения функции N(х, t) только для шага интегрирования, равного τ =120 с.
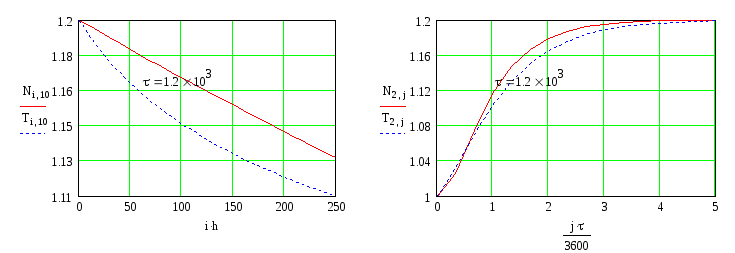
Рис. 3.27. Пространственное и временное распределение функции N(х,t)
для τ=1200 с
При увеличении временного шага до значения τ=1200 с погрешность вычисления решения гиперболического уравнения (3.3.6) по разностным схемам первого и второго порядков точности не превышает 5%, что также оправдывает применения разностных схем первого порядка точности.
Задание. Задать начальные значения функции N(0,x) и V0 из табл. 3.10 и определить максимальный шаг интегрирования τ, при котором относительная погрешность вычисления функции N(х, t), полученная на основе разностных схем, имеющих первой и второй порядки точности, не превышает 5%.
Таблица 3.10
|
Номер после-дней цифры зачетной книжки |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
N(0,x)10-26м-3 |
26 |
25 |
24 |
23 |
22 |
21 |
20 |
19 |
18 |
17 |
|
V0, м/с |
±0,001 |
±0,003 |
±0,005 |
±0,008 |
±0,01 |
±0,02 |
±0,03 |
±0,04 |
±0,05 |
±0,06 |