3. Математическое моделирование на пэвм
3.1. Системы тел сосредоточенными массами
3.1.1. Математическое моделирование теплообмена для тел сосредоточенных масс с окружающей средой
Уравнение теплообмена для тела сосредоточенной массой с окружающей средой имеет вид:
, (3.1.1)
где T0 = 100 C0 - начальное значение температуры тела; Tok = 20 C0 – температура окружающей среды; α = 0.01 c-1 скорость охлаждения тела.
Для выяснения счетной устойчивости и точности численного решения по явным и неявным разностным схемам сравним результаты численного решения уравнения (3.1) по этим схемам с его аналитическим решением [III,18]. Аналитическое решение уравнения, приведенного выше, определяется формулой:
T(t) = (T0 – Tok) e-αt + Тok . (3.1.2)
Для численного решения уравнения (3.1.1) по явным и неявным разностным схемам дискретизируем его, т. е. введем равномерную сетку по переменной t:
t0 = t0 < t1 < …<tj… < tk-1 < tk = tk, (3.1.3)
где tj = j τ; τ = ( tk ) / k; j = 0 , 1, … ,k; k = 100.
Зададим Tj = T(tj). Тогда численное решение по явной разностной схеме записывается следующим образом:
или
,
(3.1.4)
а численное решение по неявной разностной схеме имеет вид:
или
. (3.1.5)
Сравнивая численное решение дифференциального уравнения (3.1.1) по явной разностной схеме (3.1.4) на одном шаге (t = τ) c аналитическим решением (3.1.2) путем несложных преобразований, можно показать, что формула (3.1.5) совпадает с формулой (3.1.4) при условии
е-ατ = 1 - ατ , (3.1.6)
т. е. если разложить экспоненту е-ατ в ряд Тейлора, удержав нулевой и первый члены ряда, а это возможно только при условии ατ<<1 или τ<<1/α. Таким образом, явная разностная схема (3.1.4) условно устойчива (в том случае, если ατ > 1, то выражение в скобках в формуле (3.1.4) меняет знак), а точность вычислений будет определяться значением шага интегрирования по времени τ (τ<<1/α) [III, 19].
В это же время неявная разностная схема (3.1.5) является, безусловно, устойчивой, так как всегда будет выполняться условие:
.
(3.1.7)
Текст программы алгоритма решения дифференциального уравнения (3.1.1), написанной на блочно-структурном языке системы MATHCAD и числовые данные, приведены ниже.
где T, Te, Tn – решения уравнения (3.1.1), полученные на основе аналитического выражения (3.1.2) и по явной, и неявной разностных схемах, соответственно.
На рис. 3.1 приведены результаты решения обыкновенного дифференциального уравнения (3.1.1) при τ = 10с (α·τ = 0.1), а на рис. 3.2 - при τ = 200с (α·τ = 2). При этом введены следующие обозначения: Т – аналитическое решение; Те – численное решение по явной разностной схеме; Тn – численное решение по неявной разностной схеме. Сопоставление всех трех кривых при малых значениях шага интегрирования по времени τ порядка 10с указывает, как это следовало из теоретических предпосылок, приведенных выше, явная и неявная разностные схемы достаточно хорошо аппроксимируют исходное дифференциальное уравнение (3.1.1).
При больших значениях τ порядка 200с (α·τ = 2), как это обсуждалось выше, неявная разностная схема продолжает удовлетворительно аппроксимировать дифференциальное уравнение, несмотря на малое число точек (j = 3), а решение уравнения по явной схеме носит знакопеременный осциллирующий характер, что и следует из результатов численного решения дифференциального уравнения (3.1.1), приведенных на рис. 3.2.
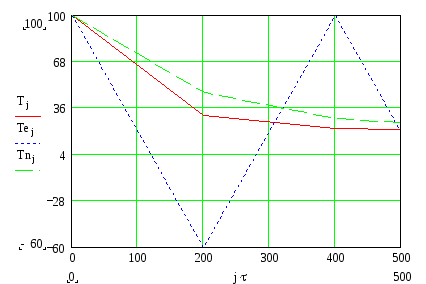
Рис. 3.1.Аналитическое решение - сплошная Рис.3.2. То же, что и на рис. 3.1,
кривая; решение по явной разностной схеме но только для шага τ = 200с
- пунктирная кривая; по неявной – штрих
пунктирная кривая, при шаге τ = 10 с
Таким образом, как это следует из теоретических и численных исследований, неявные разностные схемы являются счетно-устойчивыми для любых значений шагов интегрирования и аппроксимируют дифференциальные уравнения с первым порядком точности 0(τ), а явные разностные схемы могут быть использованы только при малых значениях шагов интегрирования, что приводит к их низкой счетной эффективности [III, 7, 10-12, 17-20].
Покажем, что первая производная температуры по времени, аппроксимирующая формулой
,
(3.1.7)
имеет первый порядок точности. Для этого разложим в ряд Тейлора дискретную функцию Тj+1 в окрестности точки j по формуле:
.
(3.1.8)
Подставляя
выражение (3.1.8) в правую часть в формулу
(3.1.7), получаем
.
(3.1.9)
Из
выражения (3.1.9) следует, что правая
разностная производная аппроксимирует
производную
в точке j
и члены бесконечного ряда порядка 0(τ),
а это и требовалось доказать.
Задание. Исследовать на сходимость явные и неявные разностные схемы численного решения уравнения теплообмена при следующих значениях T0, Tok и α:
Таблица 3.1
|
№ |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
T0 C0 |
80 |
70 |
60 |
50 |
45 |
40 |
35 |
30 |
25 |
30 |
|
TokC0 |
15 |
20 |
25 |
30 |
35 |
35 |
40 |
45 |
50 |
55 |
|
α, c-1 |
0,011 |
0,015 |
0,02 |
0,025 |
0,03 |
0,035 |
0,03 |
0,025 |
0,02 |
0,015 |