Результаты численных расчетов

Рис. 3.11. Временные распределения Рис. 3.12. Временные распределения нагрузок Р, приложенных к 1, 2 и 3-му упругих деформаций Х, приложенных позвонкам в кг/см² к 1,2 и 3-му позвонкам в мм

Рис. 3.13. Распределения нагрузок Р вдоль оси у, приложенных

к 1, 2 и 3-му позвонкам при Q=400кг и у=21мм в кг/см²

Задание. На основе приведенного выше алгоритма математической модели трехпозвонкового комплекса и коэффициентов жесткостей С, взятых из табл. 3.1 для комплексов, указанных в табл. 3.4, численно исследовать распределения упругих деформаций Х и нагрузок Р, приложенных к 1, 2 и 3-му позвонкам.

Таблица 3.4

Номер последней цифры зачетной книжки	Шейный отдел	Грудной отдел	Поясничный отдел	Целая грудная клетка
0 - 2	*****
3 - 5		*****
6 – 7			*****
8 - 9				*****

3.2. Системы с распределенными параметрами

3.2.1. Математическое моделирование процесса переноса частиц

Уравнение диффузии частиц (теплопроводности) является уравнением параболического типа и может быть записано в виде:

. (3.2.1)

Численные методы решения уравнения диффузии. С точки зрения численных методов решения уравнение диффузии частиц (3.2.1) записано в дивергентном виде, определяемое формой записи пространственной производной и позволяющее строить консервативные разностные схемы (выполнение законов сохранения на разностной сетке). В это же время, если выполнить дифференцирование, т.е.

, (3.2.2)

то для правой части равенства (3.2.2) невозможно построить консервативную разностную схему, а соответственно, такая форма записи производной не является дивергентной [III, 2, 12, 18].

Начальные и граничные условия. Начальные условия для уравнения диффузии (3.2.1) задаются в виде:

N(x; 0) = N0 = const . (3.2.3)

Граничные условия. На левой границе (х = 0 ) зададим значение концентрации, что означает приход или уход частиц в данный объем:

N(0; t) = Ψ(t) . (3.2.4)

На правой границе (х = L1) задается непроницаемость частицами поверхности стенки сосуда и моделируется следующим граничным условием:

. (3.2.5)

Таким образом, полностью сформулирована постановка задачи моделирования диффузии частиц.

Для численного решения данной краевой задачи (3.2.1), (3.2.3) – (3.2.5) воспользуемся методом прогонки. Для этого от дифференциального уравнения (3.2.1) перейдем к системе конечно – разностных уравнений. Дискретизируем задачу, т.е. вводим равномерные сетки по переменным x и t:

0 = x₀  x₁  . . .< x_i <_…  x_{n - 1}  x_n = L1, (3.2.6)

где n - число пространственных узлов; x_i = i  h; h = L1 / n; i = 0 , 1 , ..,n. Определим N_i = N(x ).

0 = t₀  t₁  . . .< t_j <…  t_{k - 1}  t_k = BP , (3.2.7)

где k - число временных слоев; t_j = j  k;  = tk / k; j = 0 , 1 , . . . , k.

Значение концентрации частиц в i-м узле и на j-м временном слое определим как N_ij =N(x_i,t_j).

Исходное дифференциальное уравнение в частных производных параболического типа (3.48) аппроксимируется конечно – разностными уравнениями во внутренних узлах по дивергентной схеме (на разностной сетке выполняются законы сохранения):

, (3.2.8)

где ; ; i = 1, 2, . . . , n – 1; j = 0, 1, . . . , k-1.

Эти разностные уравнения приводятся к каноническому трехточечному виду:

A_i N_i+1j+1 - B_i N_ij+1 + C_i N_i-1j+1 = - D_i, (3.2.9)

где ; ; ; .

Трехточечные разностные уравнения (3.2.9) запишем в виде системы трехточечных разностных уравнений для каждого i = 1, 2, . . . , n – 1 совместно с краевыми условиями:

N₀j+1 = Ψj+1 ;

A₁N₂j+1 – B₁N₁j+1 + C₁N₀j+1 = - D₁ ;

A₂N₃j+1 – B₂N₂j+1 +C₂N₁j+1 = - D₂ ; (3.2.10)

…………………………………

A_n-1N_nj+1 – B_n-1N_n-1j+1 + C_n-1N_n-2 = - D_n-1;

N_nj+1 – N_n-1j+1 = 0.

Система разностных уравнений (3.2.10) может быть записана в векторном виде:

LN = D, (3.2.11)

где ; N = ; D = .

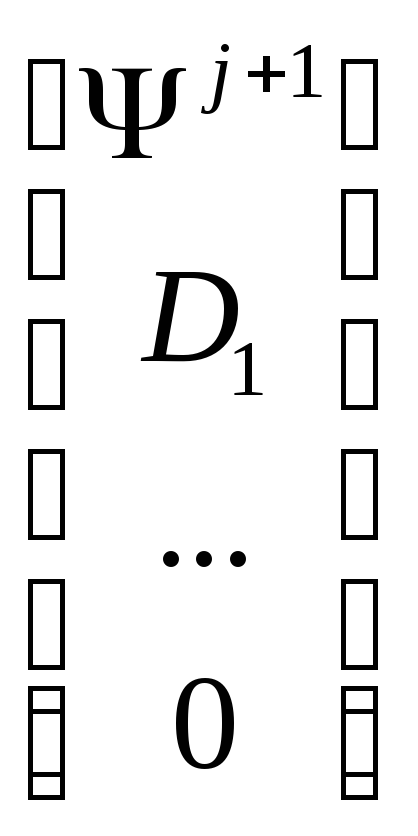Матрица L – квадратная, размером n x n, имеет трехдиагональный вид за исключением первой и последней строк, которые формируются в соответствие с заданными граничными условиями.

Наиболее эффективным методом решения системы уравнений с трехдиагональной матрицей (3.2.11) является метод прогонки.

Отметим, что критерий устойчивости численного решения к ошибкам округления для метода прогонки выполнен, если

, (3.2.12)

а значит полученная дивергентная разностная схема (3.2.12), аппроксимирующая дифференциальное уравнение (3.2.1), безусловно, устойчива и аппроксимирует его с первым порядком точности по времени и со вторым по координате.

Искомая дискретная функция N_ij+1 вычисляется по следующей рекуррентной

формуле:

N_i^j+1 = E_i+1 N_i+1^j+1 + W_i+1; i = n-1, . . . , 1, 0 , (3.2.13)

где прогоночные коэффициенты E_i+1 и W_i+1 определяются в прямом ходе i = 1, . . . , n-1:

; . (3.2.14)

Как следует из рекуррентных соотношений (3.2.14), для начала их расчета необходимо вычислить начальные значения E₁ и W₁, которые определяются с помощью левого граничного условия (3.2.4) и соотношения (3.2.5) для точки i = 0:

N₀j+1 = Ψj+1 ; (3.2.15)

N₀j+1 = E₁ N₁j+1 + W₁. (3.2.16)

Совпадение соотношения (3.2.15) с формулой (3.2.16) будет достигаться только при выполнении следующих условий:

E₁ = 0 и W₁ = Ψj+1. (3.2.17)

Правое граничное условие (3.2.5) используется для начала обратного хода i = n-1, . . . , 1, 0 по формуле, в результате которого вычисляются искомые значения концентрации N_ij+1. Запишем в разностном виде граничное условие, а соотношение (3.2.15) для точки 1 = n-1:

или ; (3.2.18)

N_n-1j+1 = E_n N_nj+1 + W_n.

Для решения системы уравнений (3.2.18), относительно , подставив значение из первого уравнения во второе, получаем:

. (3.2.19)

Текст программы алгоритма решения параболического дифференциального уравнения (3.2.1), написанной на блочно-структурном языке системы MATH CAD и числовые данные, приведен ниже.

где N- концентрация частиц.

Результаты численных расчетов. Дифференциальное уравнение диффузии частиц (2.1) численно решалось по указанному выше алгоритму при следующих исходных данных:

X_n = 1000 м; n = 100; BР = 1,728 10⁵ c; k = 100;

N_i,0 = 10²⁷ м^-3; N_0,j+1 = 1,2 1027 м^-3 ; D = 0,25 м²/с.

Необходимо отметить, что шаг интегрирования по времени τ задавался достаточно большим и составлял τ = 1728 с. Зависимость концентрации от пространственной координаты и от времени процесса приведена на рис. 3.1.3. При этом проводились численные эксперименты для нескольких значений временного шага, которые не выявили значительных погрешностей при изменении этого шага. Для упрощения записи численных значений концентраций N_i,j+1 и скоростей частиц V_i,j+1 на графиках, приведенных на рис. 3.1.3, множитель 10²⁷ опущен, и при его чтении этот множитель нужно восстанавливать.

Рис. 3.13. Зависимость концентрации от пространственной координаты и от времени процесса

Приведенный алгоритм легко реализуется на любом алгоритмическом языке и является счетно-устойчивым, наиболее счетно-эффективным и экономичным методом решения дифференциальных уравнений в частных производных параболического типа.

Задание. Провести численное исследование процесса тепломассопереноса на основе параболического дифференциального уравнения (3.2.42), при заданных начальных и граничных значениях концентрации или температур газа N(0,x), N(t,a), N(t,b) или T(0,x), T(t,a), T(t,b), а также коэффициентов диффузии D или теплопроводности λ (выбирать вариант по последней цифре зачетной книжке см. табл. 3.3).

Таблица 3.5

Номер последней цифры зачетной книжки	0	1	2	3	4	5	6	7	8	9
N(0,x) ·10-28	1	1,5	2	2,5	3	3,5	4	4,5	5	5,5
	0	0,01	0,02	0,03	-0,01	-0,02	0	0,1	-0,1	0
N(t,b) ·10-28	1,2	1	1,1	1,2	0,9	1,2	0,8	1	1	1,3
T(0,x)	70	75	80	85	90	60	50	40	30	20
	0	0,01	0,02	0,03	-0,01	-0,02	0	0,1	-0,1	0
T(t,b)	60	75	80	100	120	130	30	30	50	28
D	0,25	0,3	0,4	0,45	0,5	0,55	0,2	0,15	0,1	0,12
λ·104	1	1,5	1,7	1,9	2	3	4	5	6	7