2.2.5. Вопросы для самопроверки

1. Каким образом нужно переписать уравнение, чтобы решить его графическим методом?

2. Как найти цену делений по осям?

Лабораторная работа № 2.3 (С:\USERS\GROUP\NOF\lab3.mcd)

Решение НелинейноГо уравнениЯ МетодОм простых итераций

2.3.1. Цель работы. Получение практических навыков алгоритмизации и программирования решения нелинейных уравнений методом простых итераций.

2.3.2. Справочный материал. Любой итерационный процесс, в котором каждое последующее приближение корня уравнения определяется через предыдущее, требует знания начального приближения искомого корня, которое можно получить с помощью графического метода. Найденные в предыдущей работе значения корней уравнений мы здесь используем в качестве начального приближения. Суть метода простых итераций заключается в следующем. В исходном уравнении

F(x)=0, x₀ = const (2.3.1)

явно выразим неизвестную x:

x = f(x). (2.3.2)

Приписывая итерационные индексы неизвестной х в уравнении (2.3.2), таким образом, чтобы справа он был на единицу больше, получаем итерационный вычислительный процесс:

x_i+1 = f(x_i), x₀ = const, i = 0, 1, …, N-1. (2.3.3)

Возникает сразу два вопроса. Первый, как определить число итераций N и второй - всегда ли сходится итерационный процесс?

Первый вопрос решается на основе условия сходимости итерационного процесса

, (2.3.4)

где - малый параметр, определяющий точность вычислений.

Таким образом, итерационный процесс прерывается при начале выполнения условия сходимости (3.3.4), отсюда и определяется N как N = i+1.

Второй вопрос решается на основе условия локализации корня. Например, с помощью графика выберем окрестность искомого корня. Эту окрестность называют областью локализации корня. Итерационный процесс (2.3.3) сходится к искомому корню из любой точки области локализации, если в этой области

. (2.3.5)

Приведение исходного уравнения (2.3.1) к итерационному виду (2.3.2) в общем случае неоднозначно. Если для выбранного представления (2.3.2) условие (2.3.5) не выполняется, то нужно искать другую итерационную функцию.

2.3.3. Пример. Сначала рассмотрим уравнение с одним корнем

sin(x) – x +1 = 0.

Для него итерационную функцию запишем в виде:

p(x)=sin(x)+1. (2.3.6)

Из графика в лабораторной работе № 2.2 для области локализации корня выберем интервал [1,5; 2,5] и введем для него обозначение

Проверим условие сходимости выбранной итерационной функции (2.3.6) в области локализации искомого корня - на интервале [1,5; 2,5]:

Рис. 2.3.1. Выполнение условия локализации корня в окрестности х₀

Видно, что условие локализации в окрестности корня выполняется, и в качестве нулевого приближения возьмем х₀ = 2.

Теперь запишем алгоритм итерационного процесса вычисления корня с заданной точностью для нелинейного уравнения (2.3.1).

Рис. 2.3.2. Развитие итерационного процесса вычисления корня х_к

Как следует из рис. 2.3.2, число итераций, необходимых для их сходимости, равно N = 5, что подтверждает и выполнение условия сходимости итераций (см. табл. на рис. 2.3.2). Значение корня нелинейного уравнения (2.3.1), равно х_к = 1,93. Отметим, что корень уравнения лежит в области локализации, так как выполнено условие (2.3.5) (pf(x₅) ≤1 ).

Теперь рассмотрим уравнение

,

которое при

имеет три действительных корня.

С помощью графика из предыдущей работы выделим области локализации корней и введем обозначения для каждой из них:

x₁ (- 2,5;-1,5) r = - 2,5, - 2,3 . . -1,5

x₂ (-1,0; 0,0 ) s = -1, - 0,8 . . 0

x₃ (2,0; 3,0). t = 2, 2,2 . . 3 .

Для каждого корня нужно найти итерационную формулу вида (2.3.2) и проверить условие сходимости в соответствующей области локализации.

Пусть для x₁

.

Проверяем условие (2.3.5) сходимости для этой функции к корню x₁ в области r:

Как видно, эта функция в данном интервале не найдет корня х₁, но из функциональной зависимости производной, модуль которой уменьшается при , можно заключить, что р(х) скорее всего отыскивает х₂ . Поэтому возьмем следующий интервал, в котором находится корень х₂.

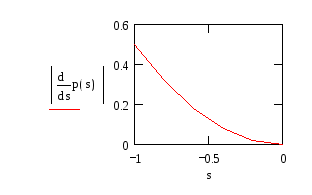
Итак, р(х) действительно находит х₂. Возвращаемся к первому корню х₁, для которого необходимо найти итерационную функцию. Здесь уместно обратить внимание на структуру корней исходного уравнения в области определения. Корень x₂ находится в окрестности х=0, а для х₁ и х₃ просматривается симметрия относительно x₂. Поэтому и функция должна быть квадратичной:

, т.е. .

Для вывода итерационной функции разделим обе части кубического уравнения на х и, извлекая квадратный корень, получим следующие зависимости:

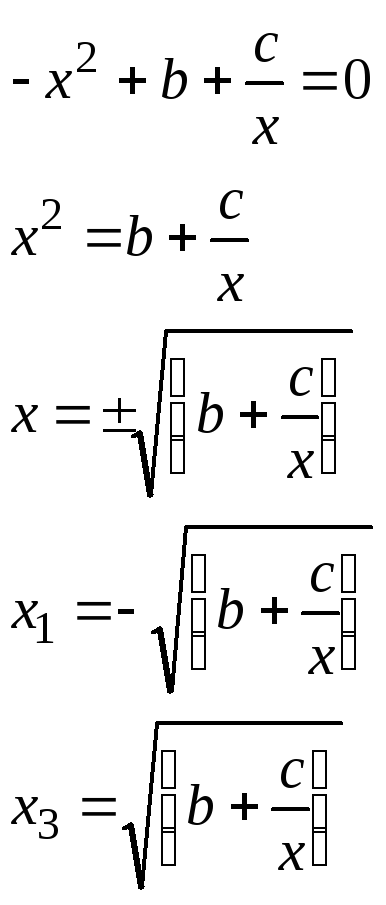
Для х₁ итерационная формула примет вид: ,

где ,

а для корня х₃ ,

где . .

Проверим выполнения условия локализации корней в соответствующих областях

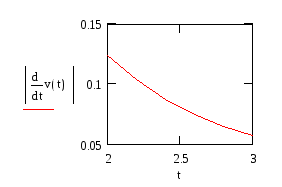
Итак, мы нашли вид итерационной функции для каждой области локализации корней. Теперь можно строить алгоритмы итерационных процессов. Находим х₁.

Рис. 2.3.3. Развитие итерационного процесса вычисления корня х1_к

Как следует из рис. 2.3.3, число итераций, необходимых для их сходимости, равно N = 2, что подтверждает и выполнение условия сходимости итераций (см. табл. на рис. 2.3.3). Значение корня нелинейного уравнения (2.3.1) равно х1_к = - 2,94. Отметим, что корень уравнения лежит в области локализации, так как выполнено условие (2.3.5) (pf(x₂) ≤1 ).

Определяем корень х2_к.

Рис. 2.3.4. Развитие итерационного процесса вычисления корня х2_к

Как следует из рис. 2.3.4, число итераций, необходимых для их сходимости, равно N = 1, что подтверждает и выполнение условия сходимости итераций (см. табл. рис. 2.3.4). Значение корня нелинейного уравнения (2.3.1), равно х1_к = - 0,11. Отметим, что корень уравнения лежит в области локализации так как выполнено условие (2.3.5) (pf(x₁) ≤1 ).

Определяем корень х3_к.

Рис. 2.3.5. Развитие итерационного процесса вычисления корня х3_к

Как следует из рис. 2.3.5, число итераций необходимых для их сходимости, равно N = 1, что подтверждает и выполнения условия сходимости итераций (см. табл.). Значение корня нелинейного уравнения (2.3.1), равно х3_к = 3.05. Отметим,что корень уравнения лежит в области локализации так как выполнено условие (2.3.5) (pf(x₁) ≤1 ).

2.3.4. Задание. Найти корни уравнения

.

Номер варианта	1	2	3	4	5	6	7	8	9	10	11
b	5,0	6,0	7,0	8,0	9,0	10,0	11,0	12,0	13,0	14,0	15,0
c	1,0	1,2	1,4	1,6	1,8	2,0	2,2	2,4	2,6	2,8	3,0