
Yuriy Kruglyak. Quantum Chemistry_Kiev_1963-1991
.pdf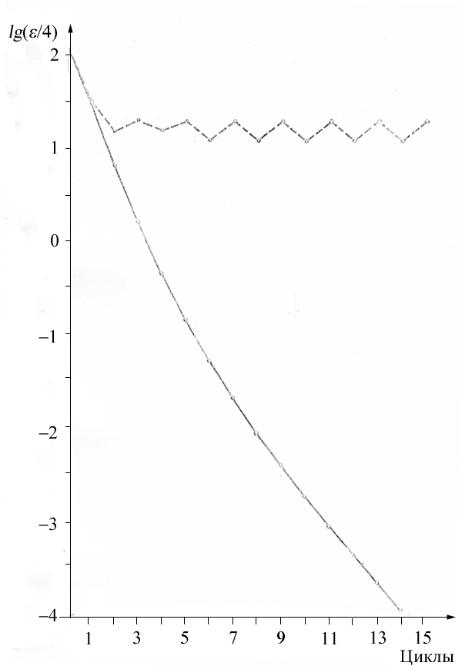
Рис. 13. Ход процесса самосогласования для триплетного состояния 5-нитроурацила: сплошная кривая получена с применением ОГ (340), а пунктирная соответствует оператору из работы [47].
Рассмотрена задача оптимизации одноконфигурационной волновой функции. Продемонстрировано, что широко использующиеся для ее решения процедуры самосогласования, основанные на гамильтонианах Фока и Рутана, являются частным случаем простейшей модификации метода ОГ. Проанализированы причины плохой сходимости итерационного процесса, основанного на использовании стандартных операторов Фока и Рутана, и продемонстрирована необходимость учета при оптимизации волновых функций свойств матрицы вторых производных энергии.
220
Литература
1.Я. И. Френкель. Волновая механика, ч. 2. Ленинград – Москва: ОНТИ – ГТТИ, 1934.
2.R. McWeeny. On the basis of orbital theories, Proc. Roy. Soc.(London),
3.T. L. Gilbert. Optimum Multiconfiguration. Self Consistent Field Equations,
J. Chem. Phys., v. 43, S248 (1965).
4.E. J. Clementi. Study of Electronic Structure of Molecules. I. Molecular Wavefunctions and Their Analysis, J. Chem. Phys., v. 46, 3842 – 3850 (1967).
5.B. O. Roos. The Multiconfigurational (MC) SCF Method In G. H. F. Dierksen and S. Wilson (eds) Methods in Computational Molecular Physics. Dordrecht: Reidel, 1983.
6.B. O. Roos, P. R. Taylor, P. E. M. Siegbahn. A complete active space SCF method (CASSCF) using a density matrix formulated super-CI approach, Chem. Phys., v. 48, 157 – 173 (1980).
7.A. C. Hurley, J. E. Lennard-Jones, J. A. Pople. The Molecular Orbital Theory of Chemical Valency: XVI. A Theory of Paired-electrons in Polyatomic Molecules,
Proc. Roy. Soc. (London), v. A220, 446 (1953).
8.R. Ahlrichs, W. Kutzelnigg. Direct Calculation of Approximate Natural Orbitals and Natural Expansion Coefficients of Atomic and Molecular Electronic Wavefunctions. II. Decoupling of the Pair Equations and Calculation of the Pair Correlation Energies for the Be and LiH Ground States, J. Chem. Phys., v. 48, 1819 (1968).
9.W. A. Goddard III, T. H. Dunning Jr., W. J. Hunt, P. J. Hay. The Generalized Valence Bond Description of the Bonding in the Low-Lying States of Molecules,
Acc. Chem. Res., v. 6, 368 – 376 (1973).
10.V. A. Kuprievich, O. V. Shramko. The method of a single-electron Hamiltonian in the single-configuration theory of a self-consistent field,
Teor. Eksper. Khim., v. 7: 6, 729 – 737 (1971).
11.V. A. Kuprievich, O. V. Shramko. Application of the single-configuration theory of
a self-consistent field to conjugated systems, Teor. Eksper. Khim., v. 7: 6, 738 – 746 (1971).
12.V. A. Kuprievich, O. V. Shramko. The MC SCF theory: method of one-electron Hamiltonian,
Intern. J. Quantum Chem., v. 6, 327 – 336 (1972).
13.V. A. Kuprievich, O. V. Shramko. Improved convergence of self-consistent procedures in the MC SCF theory, Intern. J. Quantum Chem., v. 9, 1009 – 1020 (1975).
14. R. McWeeny. Some Recent Advances in Density Matrix Theory, |
Rev. Mod. Phys., |
v. 32, 335 – 369 (1960).
15.R. McWeeny. Multi-configuration SCF calculations, Symp. Faraday Soc., v. 2, 7 – 14 (1968).
16.C. C. J. Roothaan. Self-Consistent Field Theory for Open Shells of Electronic Systems, Rev. Mod. Phys., v. 32, 179 – 185 (1960).
17.R. K. Nesbet. Configuration interaction in orbital theories, Proc. Roy. Soc. (London), v. A230, 312 (1955).
18.W. H. Adams. Orbital Self-Consistent-Field Theory. I. General Theory for Multiconfigurational Wave Functions, Phys. Rev., v. 156, 109 (1967).
19.B. Levy. Best Choice for the Coupling Operators in the Open Shell and Multiconfiguration SCF Methods, J. Chem. Phys., v. 48, 1994 (1968).
20.J. DelBene. Molecular Orbital Study of NH2, NO2, and NF2, J. Chem. Phys., v. 54, 3487 (1971).
21.Д. Р. Хартри. Расчеты атомных структур. Москва: ИЛ, 1960.
22.S. Huzinaga. Applicability of Roothaan's Self-Consistent Field Theory, Phys. Rev., v. 120, 866 (1960).
221
23. S. Huzinaga. Analytical Methods in Hartree – Fock Self-Consistent Field Theory, |
|
|
|
Phys. Rev., v. 122, 131 (1961). |
|
(1963).
25.F. W. Birss, S. Fraga. Self Consistent Field Theory. II. The LCAO Approximation,
J.Chem. Phys., v. 40, 3203 (1964).
26.G. Das, A. C. Wahl. Extended Hartree – Fock Wavefunctions: General Theory of Optimized Valence Configurations and Its Application to Diatomic Molecules,
J.Chem. Phys., v. 47, 2934 (1967).
27.A. Veillard, E. Clementi. Complete Multi-Configuration Self-Consistent Field Theory, Theor. chim. Acta, v. 7, 133 – 143 (1967).
28.G. Das, A. C. Wahl. Extended Hartree – Fock Wavefunctions: Optimized Valence Configurations for H2 and Li2, Optimized Double Configurations for F2,
J.Chem. Phys., v. 44, 87 (1966).
29.G. Das. Extended Hartree – Fock Ground State Wavefunctions for the Lithium Molecule,
J.Chem. Phys., v. 46, 1568 (1967).
30.Г. Г. Дядюша, В. А. Куприевич. Theory of the Self-Consistent Field for States with Open Shells, Теор. экспер. хим., т. 1: 3, 406 – 408 (1965).
31.R. McWeeny. In Molecular Orbitals in Chemistry, Physics, and Biology, P.-O. Lowdin and
B.Pullman, eds. New-York: Academic Press, 1964.
32.W. H. Adams. Orbital Self-Consistent-Field Theory. II. Natural Orbital Hamiltonian, Phys. Rev., v. 183: 1, 31 (1969).
33.S. Huzinaga. A General SCF Formalism, Progr. Theor. Phys., v. 41: 2, 307 – 312 (1969).
34.T. H. Brown. Quadratically Convergent Iteration Procedure for Self Consistent Calculations,
J.Chem. Phys., v. 49, 2291 (1968).
35.W. R. Wessel. Iterative Quadratically Convergent Algorithm for Solving the General Hartree – Fock – Roothaan Equations, J. Chem. Phys., v. 47, 3253 (1967).
36.D. H. Sleeman. The determination of SCF LCAO solutions for open shell configurations, Theor. chim. Acta, v. 11, 135 – 142 (1968).
37.G. Das, A. C. Wahl. Extended Hartree – Fock Wavefunctions: Optimized Valence Configurations for H2 and Li2, Optimized Double Configurations for F2,
J.Chem. Phys., v. 44, 87 (1966).
38.В. Levy. Molecular MC–SCF calculations,
Intern. J. Quantum Chem., v. 4: 3, 297 – 313 (1970).
39.N. G. Mukherjee, R. McWeeny. Multi-configuration SCF calculations on LiH, Intern. J. Quantum Chem., v. 4, 97 – 107 (1970).
40.T. A. Claxton, B. Weiner. MCSCF method in the calculation of spin density distributions, Trans. Faraday Soc., v. 66, 2113 – 2119 (1970).
41.P.-O. Lowdin. Quantum Theory of Many-Particle Systems. I. Physical Interpretations by Means of Density Matrices, Natural Spin-Orbitals, and Convergence Problems in the Method of Configurational Interaction, Phys. Rev., v. 97, 1474 – 1489 (1955).
42.О. В. Шрамко. Метод одноэлектронного гамильтониана в многоконфигурационной теории самосогласованного поля и его применение к расчету электронной структуры молекул, Канд. дисс.ИТФ АН УССР, Киев, 1972.
43.J. E. Bloor, P. N. Daykin, P. Boltwood. Theoretical studies on the electronic spectra of substituted aromatic molecules: Part II. Semiempirical self-consistent field calculations on aniline, Can. J. Chem., v. 42: 1, 121 – 136 (1964).
44.Ю. А. Кругляк, Г. Г. Дядюша, В. А. Куприевич et al. Методы расчета электронной структуры и спектров молекул. Киев: Наукова думка, 1969.24. F. W. Birss, S. Fraga. Self Consistent Field Theory. I. General Treatment,
222
45.Yu. Kruglyak. Configuration interaction in the second quantization representation: basics with applications up to full CI, ScienceRise, v. 4: 2(4), 98 – 115 (2014).
46.В. А. Куприевич, О. В. Шрамко, В. Е. Клименко. Study of the ground state of the lithium hydride molecule by the method of multiconfiguration self-consistent field theory,
Теор. экспер. хим., т. 10: 6, 746 – 755 (1965).
47.V. A. Kuprievich. SCF-CI and SCF Open-Shell Studies of the Base Components of the Nucleic Acids, Intern. J. Quantum Chem., v. 1, 561 – 575 (1967).
48.P. E. Cade, W. M. Huo. Electronic Structure of Diatomic Molecules. VI. Hartree – Fock Wavefunctions and Energy Quantities for the Ground States of the First Row Hydrides, AH,
J.Chem. Phys., v. 47, 614 (1967).
49.W. G. Richards, T. E. H. Walker, R. K. Hinkley. A Bibliography of ab initio Molecular Wave Functions. Oxford: Clarendon Press, 1971.
50.A. M. Karo. Configuration Interaction in the Lithium Hydride Molecule. II. An SCF LCAO MO Approach, J. Chem. Phys., v. 30, 1241 (1959).
51.I. G. Csizmadia, B. T. Sutcliffe, M. P. Barnett. A Group Orbital Study of Lithium Hydride, Can. J. Chem., v. 42: 7, 1645 – 1663 (1964).
52.C. F. Bender, E. R. Davidson. Theoretical Study of the LiH Molecule,
J.Chem. Phys., v. 49, 4222 (1968).
53.R. E. Brown, H. Shull. A configuration interaction study of the four lowest 1Σ+ states of the LiH molecule, Intern. J. Quantum Chem., v. 2: 5, 663 – 685 (1968).
54.R. C. Sahni, B. C. Sawhney, M. J. Hanley. Quantum mechanical treatment of molecules. Part 5. –Calculations of the potential energy curve and molecular constants of LiH (X 1Σ+ ) , Trans. Faraday Soc., v. 65, 3121 – 3128 (1969).
55.E. L. Mehler, R. Ruedenberg, D. M. Siver. Electron Correlation and Separated Pair Approximation in Diatomic Molecules. II. Lithium Hydride and Boron Hydride,
J.Chem. Phys., v. 52, 1181 (1970).
56.G. Das, A. C. Wahl. Theoretical Study of the Interaction Potential and the Hyperfine Pressure Shifts in HeH, Phys. Rev. Lett., v. 24, 440 – 443 (1970).
57.R. J. Fallon, J. T. Vanderslice, E. A. Mason. Potential Energy Curves for Lithium Hydride,
J.Chem. Phys., v. 32, 1453 (1960).
58.М. З. Балявичус, А. Б. Болотин. Лит. физ. сборник, т. 7, 713 (1967).
59.V. A. Kuprievich, V. E. Klimenko. Set of programs realizing the SCF method in the one-configuration and many-configuration approximations,
Zh. Strukt. Khim., v. 19: 4, 729 – 730 (1978).
223
224
2.9. Фермионные редуцированные матрицы плотности в квантовой химии
2.9.1.Введение
Вквантовой механике рассматриваются два вида состояний физических систем – чистые и смешанные. Первые реализуются в природе крайне редко и обычно являются физической абстракцией. Чистые состояния – это такие состояния, которые описываются волновой функцией. Для чистых состояний всегда существует такая полная система измерений, которые с достоверностью приводят к однозначно определенным результатам. Математически это эквивалентно следующему утверждению: существует такое полное множество операторов, что данная волновая функция является собственной функцией всех этих операторов.
Смешанные состояния – это состояния, описываемые матрицами плотности (МП), за исключением тех случаев, когда МП строятся из волновых функций. Для смешанных состояний не существует полной системы измерений, которые приводили бы к однозначно предсказуемым результатам.
Для математического описания произвольного состояния любой квантовомеханической системы фон Нейман [1] ввел статистический оператор или иначе, по тер Хаару [2], матрицу плотности. Физическому описанию квантовых состояний на языке МП положили начало Ландау [3] и Дирак [4]. Редуцированные матрицы плотности (РМП) для изучения свойств квантовомеханических систем были введены Хусими [5]. Однако, только после появления работ Левдина [6], МакВини [7] и Колмена [8] теория РМП стала широко применяться в квантовой механике многочастичных систем, в частности, в квантовой химии. Теории РМП и ее приложениям посвящены работы многих ученых, отметим лишь работы Местечкина [9].
Одним из наиболее важных преимуществ описания квантовых систем в формализме МП является то обстоятельство, что имеет место взаимно однозначное соответствие между физическими состояниями и множеством МП, тогда как в силу того, что состояние определяется не волновой функцией, а квадратом ее модуля и возникающей отсюда произвольностью фазового множителя, на языке волновых функций такой однозначности в общем случае нет. Другим существенным в прикладном отношении обстоятельством является тот факт, что вычисление средних значений операторов физических величин в формализме МП сводится для произвольных многочастичных систем к рассмотрению функций от гораздо меньшего и не зависящего от числа частиц системы количества переменных, что позволяет в принципе вести конкретные расчеты квантовомеханических систем с произвольным числом частиц.
Действительно, если Ψ = Ψ(x1, x2 ,..., xN ) , где x = (r, s) есть совокупность
225

пространственных и спиновых переменных, |
– волновая функция системы |
N частиц, то РМП р-го порядка (1 ≤ p < N ) , |
соответствующая N-частичной |
волновой функции Ψ , определяется как |
|
DΨp (x1, x2,..., xp; x1′, x2′,..., x′p ) = ∫Ψ(x1, x2,..., xN )Ψ(x1′, x2′,..., x′p , xp+1,..., xN )dxp+1 dxN . (421)
Гамильтониан системы запишем в стандартном виде (гл. 1)
ˆ |
N |
ˆ |
N |
HN = ∑h(i) +∑gˆ(i, j) . |
|||
|
i=1 |
|
i< j |
Тогда энергия основного состояния системы определяется как минимум функционала
E[Ψ] = ∫Ψ(x1, x2,..., xN )Hˆ N Ψ(x1, x2,..., xN ) dx1dx2 dxN ∫| Ψ(x1, x2,..., xN ) |2dx1dx2 dxN
или на языке РМП
E[D2 ] = N(N −1) Tr(Hˆ red D2 ) ,
2
где приведенный гамильтониан
ˆ |
1 |
|
|
ˆ |
ˆ |
|
+ gˆ(1,2) . |
Hred = |
N −1 |
h(1) |
+h(2) |
||||
|
|
|
|
|
|
||
Таким образом можно найти минимум функционала E[D2 ] на классе всех функций D2 (x1, x2 ; x1′, x2′) . Далее мы подробно покажем, что из определения РМП
как ядер интегральных операторов вытекают их следующие важные свойства (здесь и далее шляпку над операторами опускаем):
(а) положительная определенность для любой функции ϕ ≡ϕ(x1, x2 ,..., xp ) ,
(б) нормируемость на единицу, (в) антисимметричность, (г) эрмитовость.
Итак, варьируя E[D2 ] на классе всех D2 , удовлетворяющих условиям (а) – (г), можно вычислить энергию основного состояния системы. Именно эти прагматические цели ставились в программе, впервые сформулированной Коулсоном [10] по использованию в квантовой химии РМП преимущественно 2-го порядка и исключению волновой функции из квантовохимических расчетов из-за ее чрезмерной информативности. Впервые вариационные
226

расчеты энергии основного состояния электронного газа были проведены Майером [11]. Позднее Тредголд [12, 13] обратил внимание на ошибки математического характера в [11] и указал, что для получения физически корректных результатов необходимо кроме условий (а) – (г) наложить на класс варьируемых МП еще и другие условия. Эти, так называемые условия N-представимости состоят в том, чтобы варьируемые МП получались взятием частичного шпура из N-частичной волновой функции или совокупности N-частичных волновых функций. К сожалению, и поныне приходится констатировать, что проблема N-представимости полностью не решена даже для РМП 2-го порядка.
Мы подробно рассмотрим свойства РМП. Прежде всего для них имеет место разложение
Dp = ∑λk( p)ϕk( p)ϕk( p) . k
Если обозначить ΛmN ≡ maxk {λk(m)}, тогда для РМП имеют место также
следующие неравенства: Λ1N ≤ |
1 |
, |
Λ2N ≤ |
1 |
|
и т. д. |
|
N |
N −1 |
||||||
|
|
|
|
||||
Показано [14], например, что ранг rp как число собственных функций,
соответствующих ненулевым собственным значениям РМП р-го порядка, соответствующей антисимметричной функции от N переменных, не меньше,
чем биномиальный коэффициент N .
p
В заключение будут определены РМП перехода, необходимые для вычисления средних значений различных операторов перехода. Пусть, например, Ψ1 и Ψ2 – антисимметричные функции. Тогда, по определению,
РМП перехода р-го порядка, соответствующая функциям Ψ1 и Ψ2 , есть интегральный оператор с ядром (1 ≤ p ≤ N )
DΨp1Ψ2 (x1, x2,..., xp; x1′, x2′,..., x′p ) ≡ ∫Ψ1(x1, x2,..., xN )Ψ2 (x1′, x2′,..., x′p , xp+1,..., xN )dxp+1 dxN .
В качестве базиса гильбертова пространства H выберем слэтеровские детерминанты N-го порядка (§ 1.2.3), построенные на упорядоченном полном базисе пространства H . Для нахождения РМП перехода, соответствующих произвольным элементам пространства H , достаточно будет рассмотреть РМП перехода для однодетерминантных функций.
Здесь и далее мы в своем изложении следуем работам [15, 16], а также частично диссертации [17].
227

2.9.2. Определения
В определении фермионных РМП будем следовать [8, 18]. Пусть есть тензорное произведение гильбертова пространства H само на себя N раз, H есть пространство квадратично интегрируемых функций
от одной переменной над полем комплексных чисел С, и оператор антисимметризации (36/§ 1.2.3)
|
|
ΑN = |
|
1 |
|
|
∑ (−1)pP |
|
|||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|||||||||||
|
|
|
|
N ! P SN |
|
|
|
|
|
|
|
|
|||
или иначе оператор проектирования (Приложение П-2) |
|
||||||||||||||
|
|
ΑN: N H → ΛN H , |
|
||||||||||||
где ΛN H |
есть грассманово произведение N гильбертовых пространств Н или |
||||||||||||||
иначе |
гильбертово |
пространство |
квадратично |
интегрируемых |
|||||||||||
антисимметричных функций от N независимых переменных. |
|
||||||||||||||
В силу принципа суперпозиции нас будут интересовать лучи гильбертова |
|||||||||||||||
пространства ΛN H , т. е. множество элементов с нормой, равной единице: |
|||||||||||||||
|
Ψ ≡ Ψ(x , x ,..., x |
N |
|
) ΛN H, |
|
Ψ |
|
|
|
2 =1. |
|
||||
|
|
|
|
|
|
||||||||||
|
|
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
В дальнейшем все рассматриваемые элементы считаем лучами.
Пусть f |
p |
Λ |
p |
H |
и f |
q |
|
q |
H при p |
+ q = N. Тогда f |
p |
Λ f |
q |
ˆ |
f |
p |
f |
q |
ˆ |
||||||
|
|
|
Λ |
|
|
≡ ΑN |
|
|
ΑN |
||||||||||||||||
является грассмановым произведением |
f p и |
f q и |
f pΛ f q ΛN H . Если Ψ = f Λ g , |
||||||||||||||||||||||
то будем говорить f |
и g |
являются грассмановыми факторами элемента |
Ψ или |
||||||||||||||||||||||
просто |
факторами |
Ψ и |
|
|
что |
f делит |
|
Ψ . Лучи пространства Н называют |
|||||||||||||||||
орбиталями, а лучи пространства Λ2H – геминалями. В частности, если ϕ1 |
и ϕ2 – |
||||||||||||||||||||||||
орбитали, то ϕ1Λϕ2 |
будет геминалью. В общем случае, если ϕ1,ϕ2 ,...,ϕN – |
||||||||||||||||||||||||
орбитали, то элемент пространства |
|
ΛN H |
вида |
ϕ1Λϕ2Λ ΛϕN |
называется |
||||||||||||||||||||
детерминантом Слэтера N-го порядка. |
Для любой данной геминали |
g Λ2H и |
|||||||||||||||||||||||
для N = 2m (m – положительное целое число) через |
gN обозначим m-кратное |
||||||||||||||||||||||||
грассманово произведение |
g |
на само себя: |
gN = gΛgΛ Λg . |
Функции такого |
|||||||||||||||||||||
вида |
называются |
антисимметризованными |
геминальными |
степенями |
|||||||||||||||||||||
(АГС функции) [19]. Функции более общего вида |
Ψ = g1Λg2Λ Λgm |
|
(N = 2m) |
||||||||||||||||||||||
называются |
|
антисимметризованными |
геминальными |
|
произведениями |
||||||||||||||||||||
(АГП функции). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
228

Если f – орбиталь, то согласно [20] f ΛΨ = 0 . В общем случае, если
fделит Ψ тогда и только тогда, когда
иΨ ΛN H , то неизвестно, существует
ли достаточно простой критерий делимости (в грассмановом смысле) Ψ на f . Пусть B(Λn H ) есть множество всех линейных ограниченных операторов на
Λn H . Задав норму на B(Λn H ) в виде
|
A |
|
|
|
|
= sup |
|
ϕ |
=1 |
|
Aϕ |
|
|
|
, A B(ΛnH ) |
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ ΛnH |
|
|
|
|
|
|
|
|
B(Λn H ) можно считать банаховой алгеброй. |
|
||||||||||||||||||||
Пусть Ψ ΛN H и |
|
|
|
Ψ |
|
|
|
=1. Тогда согласно (421) определяются |
ядра |
||||||||||||
|
|
|
|
||||||||||||||||||
интегральных операторов D1(Ψ), D2 (Ψ),..., D p (Ψ),..., DN (Ψ) ≡ PΨ , где PΨ |
есть |
||||||||||||||||||||
оператор проектирования на одномерное подпространство CΨ пространства H . Очевидно, что D p (Ψ) B(Λp H ) .
По определению, оператор с ядром, найденным по формуле (421), называется фермионной РМП р-го порядка, соответствующей N-частичной функции Ψ(x1, x2 ,..., xN ) . Следуя Кумеру [21], воспользуемся символом LpN для
обозначения контракционного отображения B(ΛN H ) на B(Λp H ) . Например, если PΨ есть оператор проектирования на одномерное подпространство ΛN H , то
Lp |
P |
= Dp (Ψ) . |
|
N |
Ψ |
|
|
В общем случае |
|
|
|
Lp : Dq (Ψ) → Dp (Ψ), (q > p). |
(422) |
||
q |
|
|
|
что соответствует аналитической записи
DΨp (x1, x2 ,..., xp ; x1′, x2′,..., x′p ) ≡ ∫DΨp (x1, x2 ,..., xp , xp+1,..., xq ; x1′, x2′,..., x′p , xp+1,..., xq ) dxp+1 dxq ,
т. е. контракция Lqp связывает РМП p-го и q-го порядков, соответствующие одному и тому же элементу Ψ гильбертова пространства ΛN H .
Из определения РМП как операторов, ядра которых определяются по (421), вытекают следующие их свойства:
(а) положительная определенность, т. е. для любого элемента ϕ(x1, x2 ,..., xp ) Λp H справедливо соотношение
|
|
|
|
|
|
ϕ |
|
DΨp ϕ |
= |
|
|
(423а) |
||
|
|
|
|
|
|
|
|
|
||||||
|
|
p |
, x2 |
′ |
′ |
′ |
|
′ |
|
′ |
′ |
′ ′ |
′ |
|
|
|
|
|
|
||||||||||
= ∫ϕ(x1, x2 ,..., xp )DΨ (x1 |
,..., xp ; x1 |
, x2 |
,..., xp )ϕ(x1 |
, x2 |
,..., xp ) dx1dx2 |
dxpdx1dx2 |
dxp ≥ 0 ; |
|
||||||
доказательство этого свойства можно найти в [15, 16].
229
