Добавил:

quantum researchgate.net Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Одесский государственный экологический университет

Предмет:

Квантовая химия

Файл:

Yuriy Kruglyak. Quantum Chemistry_Kiev_1963-1991

.pdf

Скачиваний:

Добавлен:

28.02.2018

Размер:

16.43 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 6713 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

2.7.3.6. Matrix Elements of the Physical Value Operators for Molecules and Radicals with Account of Singly and Doubly Excited Configurations as an Example of General Approach

Analytical expressions for the matrix elements of the operators are useful only for simple configurations and for the derivation of various general statements. For complex configurations it is expedient to adopt a calculation scheme given above and suitable for programming. Now we give for the case of the singly and doubly excited configurations for molecules and radicals some basis vectors which will be useful in further applications [12]. They are given in a final form, and some of them are compared with the expressions available in the literature. When deriving analytical expressions for the matrix elements we did not assume any restrictions on an orthonormal orbital set used for the construction of the configurations. We also consider some general expressions for the SCF orbitals and will show that in the case of radicals some Hamiltonian matrix elements between the ground configuration and the singly excited configurations vanish. Finally, we shall give formulae for the calculation of some molecular and radical properties by the CI method such as electronic density of atoms, bond orders, transition moments, and spin distribution.

2.7.3.6.1. Basis Vectors

Consider the singly excited configurations (k,m) of a molecule with closed shells in the ground state. In this case N p = Nh =1 and four primitive vectors are possible:

Φ1

ˆ ˆ+

Φ0

Φ3

ˆ ˆ+

Φ0 ,

(207a)

= Ak+ Am+

= Ak− Am+

Φ2

ˆ ˆ+

Φ0

Φ4

ˆ ˆ+

Φ0 .

(207b)

= Ak− Am−

= Ak+ Am−

Using the rules of # 4 above one obtains

ˆ2

Φ1

−

Φ2

ˆ2

Φ3

= 2

Φ3

(208a)

, S

ˆ2

Φ2

= −

Φ1

Φ2

ˆ2

Φ4

= 2

Φ4 .

(208b)

, S

As expected, the matrix of the operator Sˆ2 reduces to one two-row and two onerow matrices. By diagonalizing the former one obtains the following normalized basis vectors

120

1Ψ1

(

Φ1 +

Φ2

MS = 0,

S = 0,

(209a)

3Ψ1

(

Φ1

−

Φ2

MS = 0,

S =1,

(209b)

3Ψ2

MS =1,

S =1,

(209c)

Φ3

3Ψ3 =

Φ4 ,

MS = −1,

S =1.

(209d)

There are unusual signs in the first two vectors.

In the case of a radical the vacuum state

Φ0

is chosen as the closed shell of its

ground state. Then one kind of the basis vectors is obviously

ˆ+

Φ0 .

(210)

Ψ1 = Am+

Now we consider the basis vectors for the configuration (k,mn) of a radical

limiting of ourselves to the vectors

with

MS =1 / 2 . The corresponding

primitive

vectors are

Φ5

ˆ+

Φ0

(211a)

= Ak− Am+ An−

Φ6

ˆ+

Φ0

(211b)

= Ak+ Am+ An+

Φ7

ˆ+

Φ0 .

(211c)

= Ak− Am− An+

When n = m , the vector

Φ6

vanishes, and the vector

Φ5 differs from

Φ7 only

by sign and becomes another basis vector

Ψ2

ˆ+

Φ0 .

(212)

= Ak− Am+ Am−

Let be n ≠ m . Writing

ˆ2

Φ j ,

(213)

Φi = ∑Sij

j=5

and using the rules of # 4 one obtains a matrix

7 / 4

−1

S2 =

−1

7 / 4

−1

(214)

−1

7 / 4

Diagonalizing this matrix we obtain eigenvector (1, –1, 1) corresponding to an eigenvalue 5/4 and two vectors (1, –1, –2) and (1, 1, 0) for degenerated eigenvalue 3/4 . Therefore the normalized doublet and quartet basis vectors are, respectively,

2 Ψ3 =		1		(		Φ5		−	Φ6 −2		Φ7 ),	(215a)



		6
	2 Ψ4	6			1		(			Φ6 )		(215b)
			=					Φ5 +


					2
					2

121

and

4 Ψ1	=	1	(	Φ5 −	Φ6 +	Φ7 ).	(216)



	3

The doublet basis vectors are determined up to a unitary transformation. We have chosen the vectors (215) to correspond to those found in the literature.

2.7.3.6.2. Elements of the CI matrix

The final expressions for the matrix elements of the Hamiltonian (31) obtained by using the results of # 5 above are now given.

Molecule

1,3

Φ0

Φ1 = − f 2Fkm ,

(217)

1,3

Φ1′

1,3

Φ1

=δkk′δmm′E0 +δkk′Fm′m −δmm′Fkk′ +2 f (km′|mk′) −(km′|k′m),

(218)

where

f =

for

S =1,

for

S = 0.

Here and in the following expressions the primes are used for numbers of those particles and holes which constitute the basis vectors placed at the left of the Hamiltonian.

Radical

Φ1′

Φ1

= δmm′E0 + Fm′m ,

′

| mm) +

Φ2

Φ2 = δkk′δmm′E0 +δmm′(2δkk′Fm′m − Fkk′) +δkk′(m m

′

+δmm′[(km

| mk ) − 2(km

| k m)],

Φ′

= δ

′(δ

′δ

′ −δ

′δ

′)E

{δ

′(2δ

′F ′

+ 2δ

′F ′

+δ

′F ′

+δ

′F ′

) −

n n

m m

m n

n m

− Fkk′(2δmm′δnn′

′

+δmn′δnm′) +δkk′[2(m n

| mn) + (m n

| nm)] − 2δmm′(kn

| k n) +

′

+δnn′[3(m k

| k m) −

2(m k

| mk )] −δmn′(m k

| nk ) −δnm′

(n k | mk )},

Φ′

= δ

′(δ

′δ

′ −

′δ

′)E

{δ

′(2δ

′F ′

+ 2δ

′F ′

−δ

′F ′

−δ

′F ′

) −

n n

m m

m n

n m

−Fkk′(2δmm′δnn′ −δmn′δnm′) +δkk′[2(m′n′| mn) − (m′n′| nm)] + 2δmm′[2(kn′| nk′) −

−(kn′| k′n)] +δnn′[(m′k | k′m) − 2(m′k | mk′)] +δmn′[(m′k | nk′) − 2(m′k | k′n)] + +δnm′[(n′k | mk′) − 2(n′k | k′m)]},

(219)

(220)

(221)

(222)

2	Φ1′	ˆ	2	Φ2	= δmm′Fkm + (km′\| mm) ,	(223)

		H

122

Φ1′

Φ3

δnm′Fkm +

(km′| mn) ,

Φ1′

[2δmm′Fkn −δnm′Fkm + 2(km′| nm) − (km′| mn)],

Φ4

′

′ ′

′

′ ′

Φ3

Φ2

{δkk′[(m m

| mn) − (m m

| nm)] + 2δmm′(km

| nk )

− 2δnm′(m k | k m)},

′

′ ′

Φ4

{δkk′(δmm′Fm′n +δnm′Fm′m )

| mn) +

Φ2

−δnm′δmm′Fkk′ +δkk′(m m

′

′ ′

′

+δmm′[2(km

| nk ) − (km

| k n)] −δnm′[(m k | k m)

+ (m k | mk )]},

Φ′3

Φ4

{δkk′(δmm′Fn′n +δnn′Fm′m −

δmn′Fm′n −δnm′Fn′m ) − Fkk′(δmm′δnn′ −δmn′δnm′) +

+δkk′[(m′n′| mn) − (m′n′| nm)] +δmm′[2(kn′| nk′) − (kn′| k′n)] +

+δnn′[(m′k | k′m) − (m′k | mk′)] +δmn′[(m′k | nk′) − 2(m′k | k′n)] +

+δnm′[(n′k | mk′) − (n′k | k′m)]}.

(224)

(225)

(226)

(227)

(228)

Formula (219) is well known, e.g. in [13, 14]. Particular cases of some of the general expressions above can be found in the quantum chemistry literature, e.g. formula (220) for k′ = k,m′ = m and (222) for k′ = k,m′ = m,n′ = n in [13], formula (223) for m′ ≠ m in [13] and for m′ = m in [14], formula (224) for m′ = m in [14].

2.7.3.6.3. Brillouin Theorem and its Analog for Radicals

The orthonormal orbitals for which the first variation of energy E0 of the vacuum state Φ0 vanishes according to [15] satisfy the operator equation

ˆ ˆ

(229)

− PF = 0 ,

is the Fock – Dirac density operator

where F is the Fock operator, and

ϕl

(230)

∑

l=1

and ϕm and using

Calculating the matrix element of (229) over the orbitals ϕk

projection properties of the operator

one

obtains from (217)

if initial orbitals

satisfy equation (229) that

Φ0

Φ1

= 0 .

(231)

The conditions used in deriving (231) are more comprehensive than the conditions of the well known Brillouin theorem [16, 17]. The content of this theorem

123

is expressed by (231) if configurations are built on the SCF eigenfunctions of the
operator F .
ˆ
In the case of a radical the orbitals for which the first variation of the energy of
the configuration (−,m) vanishes satisfy the operator equation [19]
	ˆ	ˆ	ˆ		ˆ	ˆ	ˆ	ˆ	ˆ	(232)
	F P		− PF + F P − P F = 0 ,							(232)
	1	1		1	1	2	2	2	2
where P1 is defined by (230),		P2	is a projection operator for the orbital ϕm , and the
ˆ		ˆ
operators F1 and	F2 for a semi-open shell are determined as
ˆ	ˆ
			ˆ		ˆ	ˆ		1 ˆ		(233)
			F1	= F		+ J	0 −	2 K0 ,		(233)
			ˆ		1	ˆ	ˆ	ˆ		(234)
			F2	= 2 F + J0				− K0		(234)

with the Fock operator

built

the vacuum

orbitals, and Coulomb

J0 and

exchange K0 operators are built on the orbital ϕm .

Let us write down the expressions for the matrix elements (219) for m′ ≠ m and

(223), (225) for m′ ≠ m,n ≠ m

Φ1

Φ1′ = Fmm′

(235)

Φ1

Φ2

(236)

= Fkm +(J0)km ,

Φ1

Φ4

(237)

2[Fkn +(J0)kn

− 2

(K0)kn ],

where the last two matrix elements are expressed over the matrix elements of the

operators J0

and K0 on the orbitals ϕi .

Using projection properties of the operators

P1 and P2

ϕk

ϕk ,

ϕm

ϕm′

ϕn

= 0,

(238a)

= P1

ϕm

ϕk

ϕm′

ϕn

= 0

(238b)

,P2

= P2

from equation (232) one obtains

ϕm

ϕm′

= 0,

ϕk

ϕm

= 0,

(239)

− F2

ϕk

ϕn = 0.

Substituting Fˆ1 and Fˆ2 according (233) to (239) and using the identity

ˆ	ϕm	ˆ	ϕm	(240)

J0		≡ K0

124

ψ p Qˆ ψq

(−,m)

we see that relations (239) express that the right sides of the equations (235) – (237) are zero.

Thus, the following statement was proved. If the configurations are built on an orthonormal orbital set for which the first variation of an energy of the configuration vanishes, then the Hamiltonian matrix elements between this configuration and any of the configurations (−,m′) with m′ ≠ m , configuration (k,mm) , and of the

vector (215b) of the configuration (k,mn) with n ≠ m are equal to zero.

Generally the equation (232) has many solutions but the statement proved so far is valid for any particular solution irrespective of the procedure of its derivation. Thus, this statement remains valid for the SCF orbitals obtained by the Roothaan operator [19] or by the use of the one-electron Hamiltonian for one open shell [20].

2.7.3.6.4. Calculation of Certain One-particle Properties

The wave function for the state λ in the CI method is expanded over the basis vectors

λ = ∑Xqλ	ψq	(241)

q

and the MO ϕi used to construct the primitive vectors are usually expressed as linear combination of orthonormal AO

ϕi = ∑Cµi χµ .	(242)
µ

Observable physical properties are determined by the matrix elements mostly of the one-particle operator Qˆ

κ	ˆ		*	ψ p	ˆ	ψq .	(243)


	Q	λ = ∑X pκ Xqλ			Q
			pq
Thus, one first needs to calculate the matrix elements of Q on the basis vectors.
If Q is a spin-free operator,			analytical			ˆ	for the matrix elements
				expressions
ˆ

for the configurations considered so far are obtained directly from the Hamiltonian matrix elements (217) – (228) by ignoring two-electron terms and

changing Fij to Qij and F0		to an average value			ˆ
changing Fij to Qij and F0		to an average value		Q0 of the operator Q in the vacuum
state. In particular, for the calculation of the electronic density on					atoms Pµµλλ	and
bond orders Pµνλλ	in a state	λ	as well as transition electronic density on atoms			Pµµκλ
corresponding to	a transition		from state κ to	state λ one must	take Cµ*iCµ j	and
correspondingly Cµ*iCν j ≡ Pij		instead of Qij and Q0			nF
correspondingly Cµ*iCν j ≡ Pij		instead of Qij and Q0		must be put equal to 2∑Cµ*iCνi .
					i=1

125

In the zero differential overlap approximation a component of the transition moment are determined through corresponding atomic coordinates and transition density, for example:

µχκλ = ∑χν Pννκλ .	(244)
ν

When calculating the spin density ρµνλ in a state λ one meets with an operator Qˆ

which according to formula (172) depends on the spin variables being diagonal over them. We give final expressions for the matrix elements needed to calculate the spin density denoting

Cµ*iCν j ≡ Pij ,

namely:

3Ψ1′ 2Sˆz 3Ψ1 =δkk′Pm′m +δmm′Pkk′,

2 Ψ1′ 2Sˆz 2 Ψ1 = Pm′m

2 Ψ′2 2Sˆz 2 Ψ2 =δmm′Pkk′

2	Ψ′3		ˆ	2		Ψ3 =	1					(4δmm′Pn′n − 2δnn′Pm′m −δmn′Pm′n −δnm′Pn′m ) − Pkk′(4δmm′δnn′ −5δnn′δnm′)],
2			ˆ	2			1
		2Sz					6 [δkk′
							6 [δkk′
2	Ψ′4		ˆ		2	Ψ4	=	1			[δkk′(2δnn′Pm′m −δmn′Pm′n −δnm′Pn′m ) − Pkk′(δmm′δnn′ −δmn′δnm′)],
2			ˆ		2			1
			2Sz					2
2			ˆ		2			2
	Ψ1′					Ψ2	= −δmm′Pkm

			2Sz
2			ˆ		2					1
2			ˆ		2					1
	Ψ1′		2Sz			Ψ3	= −									(2δmm′Pkn +δnm′Pkm )

												6
												6
2			ˆ		2					1
2			ˆ		2					1
	Ψ1′		2Sz			Ψ4	= −									δnm′Pkm

													2
2			ˆ		2			1					2


	Ψ′2		2Sz			Ψ3	=							[δkk′(δmm′Pm′n −δnm′Pm′m ) +3Pkk′δmm′δnm′],

										6
										6
2			ˆ					1
2			ˆ					1
	Ψ′2		2Sz			Ψ4	=							[δkk′(−δmm′Pm′n +δnm′Pm′m ) + Pkk′δmm′δnm′],

											2
											2
2			ˆ		2			1
2			ˆ		2			1
	Ψ′3		2Sz			Ψ4	=								[δkk′(−δmn′Pm′n +3δnm′Pn′m ) + Pkk′(2δmm′δnn′ +δmn′δnm′)].

									12
									12

(245)

(246)

(247)

(248)

(249)

(250)

(251)

(252)

(253)

(254)

(255)

(256)

126

3ρµµλ

The expression for derived in [9, 21] by the determinantal method is obtained from (246) in a way described above.

2.7.3.7. Exact Solution for a Seven-electron System Using Full CI

General approach to calculation of the CI matrix elements (# 5 above) was also used to perform full CI computation which gives an exact solution for a model

Hamiltonian used. The full CI calculation was done for π-electronic model of the benzyl radical containing seven π-electrons. The reason why just the benzyl radical was chosen to perform such a labor-consuming full CI computation is connected with a still not-resolved discrepancy between computed π-spin density distribution in benzyl radical and its ESR proton splitting well studied experimentally [22, 23]. This being the situation when it seems desirable to examine the different characteristics of the ground state of benzyl radical as the approximation for the wave function is improved and approaches an exact eigenfunction of a given π-electronic Hamiltonian. We focus in this review only on technique how the restricted up to the full CI calculations were practically performed.

For a π-electronic shell of benzyl radical we used the traditional model based on the zero differential overlap approximation. Introducing creation aˆµσ+ and annihilation

aˆµσ operators for an electron in atomic state µ with the spin σ and using the second quantization representation, the corresponding Hamiltonian is

ˆ	core	+	1	∑	+	+	(257)
H = ∑hµν		aˆµσ aˆνσ +	2	∑	γµν aˆµσ aˆνσ′aˆνσ′aˆµσ ,		(257)
µνσ			2	µνσσ′
where hµνcore are so called	core	integrals,		and	γµν –	electron repulsion	integrals of

π-electronic theory. Indexes µ and ν run over all AOs (in our case from 1 to 7), and spin indexes σ and σ′ take values +1/2 or –1/2. Regular model of the benzyl radical with standard CC bond length equal to 1.4 Å was used. All data which define the Hamiltonian (257) completely can be find in [22]. Full CI was also performed for “equillibrium” model of the benzyl radical [23] (Appendix П-7).

Now it is proper for computations to pass from AOs to MOs. Formally, this can

be done by the introduction of creation	ˆ+	and annihilation	ˆ	operators for
be done by the introduction of creation	aµσ	and annihilation	aµσ	operators for
electrons in molecular states through the canonical transformation
ˆ	+	* ˆ+		(258)
aˆµσ = ∑Cµi Aiσ ,	aˆµσ	= ∑Cµi Aiσ ,		(258)
i		i
where Cµi are expansion coefficients of MO i		over AOs. It is necessary that these

expansion coefficients form a unitary matrix. Thus, the MOs will be orthonormalized

127

and the commutation properties of the operators					Aiσ and		Aiσ will have the standard
					ˆ+		ˆ
form.
Substituting (258) into (257) one obtains
ˆ	ˆ+ ˆ	1	∑	ˆ	+ ˆ+	ˆ	ˆ	(259)
H = ∑hij Aiσ Ajσ +			∑	(ij \|kl)Aiσ Ajσ		′Alσ′	Akσ ,	(259)
	ijσ	2 ijklσσ′
where	hij = ∑Cµ*iCν jhµνcore ,
	hij = ∑Cµ*iCν jhµνcore ,							(260)
		µν
	(ij \|kl) = ∑CµiCµkCν jCνl γµν .							(261)
	µν

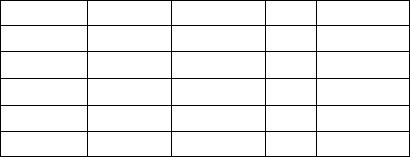
In our computations the Hamiltonian (259) was taken as initial one. For the MOs entering (260) and (261) we have chosen those which minimize the energy of the ground configuration of benzyl. The corresponding orbital coefficients computed by the SCF method for an open shell configuration [9] are shown in Table 6.

Choice of these orbitals seems to be most natural providing conservation of the alternant properties for the full as well as for certain truncated configurational sets. These orbitals possess proper symmetry and some of the CI matrix elements are zero [12] due to relations analogous to Brilloiun’s theorem. It should be noted that the results obtained with full CI are invariant to the choice of the basis orbitals [1].

Table 6

SCF open shell MO coefficients Cµi of benzyl radical*

µ \ i =	1	2	3	4
1	0.465960	0.531866	0	0
2	0.414531	0.201041	–0.5	–0.274759
3	0.376086	–0.329484	–0.5	0
4	0.356471	–0.592641	0	0.208348
7	0.171045	0.260654	0	0.897555

*Remaining coefficients are determined by symmetry of MOs and due to alternant properties of benzyl radical.

2.7.3.7.1.Configurations and Details of Computation

In the framework of the CI method the wave function is improved simply by extension of the configurational set. With a full set of configurations, the number of which is finite in our case, one obtains an exact eigenfunction for a given model Hamiltonian.

128

2B2 . In the π-electron

The theory of the CI method is well known [1]. The wave function is expanded in Slater determinants. The expansion coefficients are determined by diagonalization of the CI matrix. Its order can be lowered essentially if instead of single Slater determinants their orthonormal linear combinations of proper symmetry and multiplicity are used. We utilized this general scheme using the second quantization formalism described above successively, which is equivalent to the traditional determinantal Slater approach.

The ground state configuration of benzyl has symmetry

approximation there are 212 excited configurations of the same symmetry. The distribution of these with the multiplicity of the excitation and with the number of unpaired electrons is given in Table 7.

For each configuration one can form one or more orthonormal doublet basis vectors corresponding to a positive projection of the spin. Construction of such single

vector for the configuration (i)2 ( j)2 (k)2 (l)1					is simple. This vector corresponds to a
single Slater determinant and is written as
A+	A+	A+	A+	A+ A+ A+			0 ,	(262)

iα	iβ	jα	jβ		kα	kβ lα

where 0 is the vacuum state, and indices α and β denote values +1/2 and –1/2 of

the spin variable σ .

Table 7 Number of excited configurations for the benzyl radical

depending on their type

with corresponding number of the basis vectors (in parenthesis).

Number of		Multiplicity of excitation
unpaired
unpaired	1	2	3	4	5	6
electrons	1	2	3	4	5	6

1	4(4)	21(21)	24(24)	33(33)	12(12)	5(5)

3	5(10)	14(28)	36(72)	22(44)	13(26)	–

5	–	5(25)	8(40)	9(45)	–	–

7	–	–	1(14)	–	–	–

Σ	9(14)	40(74)	69(150)	64(122)	25(38)	5(5)

The configuration (i)2 ( j)2 (k)1(l)1(m)1 with three unpaired electrons gives rise to three vectors of type (262) with MS = +1 / 2 :

129

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 6713 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете Квантовая химия

#
28.02.201830.33 Mб3Kruglyak_Whitman.Tables_of_Quantum_Chemistry_Integrals_V.1.pdf
#
28.02.201816.43 Mб28Yuriy Kruglyak. Quantum Chemistry_Kiev_1963-1991.pdf