
Yuriy Kruglyak. Quantum Chemistry_Kiev_1963-1991
.pdfМатрица P является полноценной проектирующей (на подпространство занятых орбиталей) матрицей только в том случае, если базисные функции {χµ}
ортонормированы. В общем же случае, когда Sµν = χµ | χν ≠ δµν , матрица
плотности эрмитова, но не идемпотентна, а свойством идемпотентности обладает матрица PS = (PS)2 . Действительно,
|
n |
n |
n |
n |
n |
(PS)2 |
= PSPS = ∑cici†S∑cjc†j |
S = ∑cici†Scjc†j |
S = ∑ciδijc†j |
S = ∑cici†S = PS , (119) |
|
|
i=1 |
j=1 |
i, j=1 |
i, j=1 |
i=1 |
где мы учли, что занятые орбитали ортонормированны:
m |
m |
m |
=ci†Scj =δij. |
|
|
ϕi |ϕj = ∑cµiχµ |∑cνiχν = ∑ cµiSµνcν j |
(120) |
||||
µ=1 |
ν=1 |
µ,ν |
=1 |
|
|
Умножая обе стороны равенства |
PSPS = PS |
справа на матрицу S−1 , |
которая |
||
существует, поскольку невырождена, имеем иную запись идемпотентности в форме PSP = P . Поскольку матрица S в ортонормированном базисе равна единичной матрице, то матрица P в этом случае сама является идемпотентной проектирующей матрицей.
В методе НХФ вводят две матрицы плотности: одну для орбиталей со
спином α , а другую для орбиталей |
со |
спином β . |
Пусть коэффициенты |
||
разложения для орбиталей |
| ai |
и |
| bi |
задаются |
векторами ai и bi , |
соответственно: |
|
|
|
|
|
m |
|
|
|
m |
|
|ai = ∑aµi |
|χµ , |
|bi = ∑bµi |χµ , |
(121) |
||
µ=1 |
|
|
|
µ=1 |
|
тогда |
|
|
|
|
|
n |
|
|
n |
|
|
Pµνa = ∑a aµiaνi , |
Pµνb |
= ∑b bµibνi |
(122) |
||
i |
=1 |
|
|
i=1 |
|
или в матричной записи |
|
|
|
|
|
|
n |
|
|
n |
|
Pa = ∑a aiai†, |
Pb = ∑b bibi† . |
(123) |
|||
|
i=1 |
|
|
i=1 |
|
2.5.2. Матрица Фока и энергия
Сначала рассмотрим случай ОХФ. Элементы матрицы Фока в (112)
ˆ |
ˆ |
n |
ˆ ˆ |
n |
ˆ |
ˆ |
|
|
|||||
Fνµ = χν | F | χµ = χν | h |
+ ∑(2Ji − Ki ) | χµ = hνµ + ∑(2 χν | Ji | χµ − χν | Ki | χµ ) .(124) |
|||||
|
|
i=1 |
|
i=1 |
|
|
90
Кулоновский матричный элемент, согласно (74),
χν | Jˆi | χµ = ∫χν (1)(∫ϕi (2)r12−1ϕi (2)dv2 )χµ (1)dv1 =
= ∫∫χν (1) |
|
m |
|
|
|
m |
|
|
|
|
∑cρi χρ |
(2) |
r12−1 |
∑cτi χτ (2) χµ (1)dv1dv2 |
= |
(125) |
|||
|
|
ρ=1 |
|
|
|
τ=1 |
|
|
|
m |
∫∫ |
χν (1)χρ |
(2)r12−1χµ (1) |
m |
ρ,τ=1 |
ρ,τ=1 |
|||
= ∑ cρicτi |
|
χτ (2)dv1dv2 = ∑ cρicτi[χν χρ | χµχτ ]. |
Аналогично, согласно (76), переписывается обменный матричный элемент:
m
χν | Kˆi | χµ = ∑ cρicτi[χν χρ | χτ χµ ]. . (126) ρ,τ=1
Подставляем (125) и (126) в (124) и пользуемся (116), тогда
Fνµ = hνµ + |
n |
|
2 |
m |
c c |
[χν χρ | χµχτ ]− |
m |
c c |
[ |
|
|
|
|
∑ |
∑ |
χν χρ | χτ χµ ] |
= |
||||||
|
∑ |
|
ρi τi |
|
ρi τi |
|
|
(127) |
|||
|
i=1 |
|
|
ρ,τ=1 |
|
|
ρ,τ=1 |
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
= hνµ + ∑ Pτρ (2[χν χρ | χµχτ ]−[χν χρ | χτ χµ ]), |
|
|
|||||||||
|
ρ,τ |
=1 |
|
|
|
|
|
|
|
|
|
откуда видно, что для вычисления элементов матрицы Фока нужны матрица плотности P , одно- и двухэлектронные интегралы.
Для метода НХФ аналогичные выкладки дают
|
m |
|
Fνµa |
= hνµ + ∑ |
(Pτρa + Pτρb )[χν χρ | χµχτ ]− Pτρa [χν χρ | χτ χµ ] , |
|
ρ,τ=1 |
(128) |
|
m |
|
Fνµb |
= hνµ + ∑ |
(Pτρa + Pτρb )[χν χρ | χµχτ ]− Pτρb [χν χρ | χτ χµ ] . |
|
ρ,τ=1 |
|
Несколько слов об обозначении двухэлектронных интегралов и их симметрии. Для интегралов
[χµχν | χρ χτ ] ≡ χµ (1)χν (2) | r−1 |
| χρ (1)χτ (2) |
(129) |
12 |
|
|
удобно использовать обозначение [12|34], поскольку оно позволяет различать сомножители из бра-скобки и из кет-скобки. Если же используются вещественные орбитали, как это обычно имеет место при выполнении вычислений на компьютерах, тогда двухэлектронные интегралы удобнее обозначать (11|22), а именно:
(χµχν | χρ χτ ) ≡ ∫∫χµ (1)χν (1)r12−1χρ (2)χτ (2)dv1dv2 =[χµχρ | χν χτ ]. |
(130) |
91
Из определения (130) очевидна инвариантность такой записи по отношению к перестановкам орбиталей χµ с χν и χρ с χτ , а также двух наборов
орбиталей, соответствующих переменным интегрирования 1 и 2. Обозначая для краткости (χµ χν | χρ χτ ) , как (µν | ρτ) , имеем равенства:
(µν | ρτ) = (νµ | ρτ) = (µν |τρ) = (νµ |τρ) = (ρτ | µν) = (ρτ |νµ) = (τρ | µν) = (τρ |νµ). (131)
Эту симметрию можно почувствовать, если рассматривать интеграл (130) как электростатическое взаимодействие двух зарядовых плотностей χµ (r1)χν (r1) и
χρ (r2 )χτ (r2 ) .
Всоответствии с цепочкой равенств (131), если все четыре индекса различны, то существует восемь интегралов, порядок индексов у которых в определении (130) различен, но значения их равны. При одной паре совпадающих индексов это число уменьшается до четырех, а при двух совпадающих парах – до двух, и до единицы, если все индексы одинаковы.
Используя элементы матрицы плотности D (118), а также обозначения (130), элементы фоковской матрицы в методе ОХФ вместо (127) записываются как:
m |
1 |
|
|
Fνµ = hνµ + ∑ Dτρ[(χν χµ | χρ χτ ) − |
(χν χρ | χµχτ )], |
(132) |
|
ρ,τ=1 |
2 |
|
|
которое можно получить из его аналога (128) для метода НХФ если учесть, что в случае ОХФ
Pa = Pb = 1 D . |
(133) |
2 |
|
Электронную энергию однодетерминантной функции в случае НХФ, согласно (93), можно записать следующим образом:
|
|
1 |
na |
|
m |
|
µi |
ˆ ˆ a |
|
m |
|
νi |
|
nb |
|
|
m |
µi |
|
|
ˆ |
ˆ b |
|
m |
|
|
|
|
|
|
|
|
|
||
E = |
2 |
|
∑ |
|
∑ |
a |
χµ |h + F |
∑ |
|
χν + |
∑ |
|
∑ |
χµ |
|h |
+ F |
∑ νi |
χν |
|
= |
|
|
|||||||||||||
|
|
|
|
|
| |
|
a |
|
|
|
b |
| |
|
|
b |
|
|
|
|||||||||||||||||
|
|
|
i=1 µ=1 |
|
|
|
ν =1 |
|
|
|
i=1 µ=1 |
|
|
|
|
|
ν =1 |
|
|
|
|
|
|
|
|||||||||||
|
= |
1 |
|
na |
|
m |
|
|
ˆ |
|
ˆ a |
|
nb |
m |
|
|
|
|
|
ˆ |
ˆ b |
|
|
|
= |
|
|
|
|
|
(134) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
2 |
|
∑ ∑ aµiaνi χµ |h + F |
|
|χν +∑ ∑ bµibνi χµ |
|h + F |
|
|χν |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
i=1 µ,ν =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
i=1 µ,ν =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
= |
1 m |
|
a |
|
|
a |
b |
|
|
|
b |
|
= |
1 |
|
|
a |
(h + F |
a |
|
+Tr |
|
|
b |
(h + F |
b |
|
||||||||
2 µ∑,ν =1 Pµν (hµν |
+ Fµν ) + Pµν (hµν |
+ Fµν ) |
2{Tr P |
|
|
) |
P |
|
|
|
) }. |
||||||||||||||||||||||||
|
|
|
В случае ОХФ выражение для энергии упрощается до |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E = 1 Tr[D(h + F)]. |
|
|
|
|
|
|
|
|
|
|
|
|
(135) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
92
Подставляя выражения для элементов матрицы Фока (132) в (135), получаем электронную энергию в виде
m |
1 |
m |
|
|
1 Dρν Dτµ )(χν χµ | χρ χτ ) , |
|
E = ∑ Dµν hνµ + |
∑ |
(Dµν Dτρ − |
(136) |
|||
µ,ν =1 |
2 |
µ,ν,ρ |
,τ=1 |
|
2 |
|
в котором последнее слагаемое в обменной части матрицы Фока получено перестановкой индексов µ и ρ .
2.5.3. Метод ОХФО для открытых оболочек
Однодетерминантный метод НХФ часто используется для расчета молекулярных систем с открытыми электронными оболочками, таких как свободные радикалы (дублетные состояния) и триплетные состояния молекул. Его основной недостаток состоит в том, что волновая функция в этом методе не является собственной функцией оператора полного спина.
В методе ОХФО/ROHF замкнутые и открытые оболочки описываются по разному. Первые состоят из дважды занятых орбиталей и их расщепление не предполагается, а в случае открытых оболочек структура волновой функции определяется характером открытой оболочки. Так, волновая функция может быть однодетерминантной как в случае дублета или высокоспиновой компоненты триплета. Может быть и линейной комбинацией двух и
более детерминантов как, например, для синглета с открытой оболочкой (бирадикал в синглетном состоянии) или компоненты триплет с Sz = 0 .
В методе ОХФО разные случаи открытых оболочек описываются единообразно на основе достаточно общего выражения для энергии с численными коэффициентами для разных ситуаций. Считается, что мы имеем дело с некоторым числом N ортонормированных пространственных орбиталей ϕi , каждой из которых можно сопоставить присущее ей число заполнения ωi ,
так что общее выражение для энергии будет таким:
N |
N |
|
E = ∑ωihii + ∑(αij Jij − βijKij ) , |
(137) |
|
i=1 |
i, j=1 |
|
где коэффициенты связи αij и βij определяются структурой открытой оболочки.
Суммирование по i и по j выполняется |
независимо, |
ˆ |
есть |
hii = ϕi | h |ϕi |
|||
матричный элемент одноэлектронной части |
гамильтониана, Jij = [ϕiϕj |ϕiϕj ] – |
||
кулоновский интеграл, а Kij = [ϕiϕj |ϕjϕi ] – обменный.
Выражение для энергии (137) достаточно общее. Оно соответствует волновой функции ОХФ замкнутой оболочки при значениях параметров
93
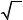
N = n, ωi = 2, αij = 2, βij =1,
как и функции НХФ при
N = na +nb, ωi =1, αij =1/ 2, βij =1/ 2,
если i и j оба принадлежат к одному набору {ai} или {bi}, и βij = 0 в противном
случае.
Приведем значения коэффициентов связи для наиболее важных случаев открытых оболочек.
В простейшем случае высокоспиновой открытой оболочки (дублет, триплет с Sz =1) достаточно однодетерминантной волновой функции. В этом
случае имеем замкнутую оболочку с nc дважды занятыми орбиталями, а поверх нее открытую оболочку с no орбиталями, однократно занятыми электронами со
спином α . Энергию такой системы легко получить из общей формулы (87) для однодетерминантной волновой функции, подставляя в нее
nb = nc, na = nc +no, ap = bp =ϕp ( p ≤ nc ) иap =ϕp (nc +1≤ p ≤ nc +no ),
а именно:
nc |
nc +no |
nc |
nc nc +no |
|
E = ∑2hpp + |
∑ hqq + ∑ |
(2J pq − Kpq ) +∑ ∑ |
(2J |
|
p=1 |
q=nc +1 |
p,q=1 |
p=1q=nc +1 |
|
Коэффициенты, введенные в (137), таковы:
ωc = 2,ωo =1,αcc = 2,αco =αoc =1,αoo =1/ 2,
1 nc +no
pq − Kpq ) + 2 p,q∑=nc +1(J pq − Kpq ).(138)
βcc =1, βco = βoc = βoo =1/ 2,
где индексы с и о указывают на закрытую оболочку {С} или открытую {О}, к
которой принадлежат орбитали ϕi ,ϕj |
. При определении этих коэффициентов |
||
учитывалось, что суммирование по i |
и j |
в (137) выполняется независимо, так |
|
что существует |
случай, когда i {C} |
и |
j {O}, как и случай когда j {C} и |
i {O}. В случае |
дублетного состояния (no |
=1) в открытой оболочке есть только |
|
одна орбиталь и последняя сумма в (138) исчезает (J pp ≡ Kpp ) .
В случае открытой оболочки, описываемой двумя детерминантами, с двумя электронами в синглетном или в триплетном состоянии с Sz = 0 имеем:
1,3Ψ = |
1 |
(Ψ ± Ψ |
|
) , |
|
(139) |
||||||||
|
|
|
||||||||||||
|
|
|
2 |
|
|
1 |
|
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
2 |
|
2 |
2 |
ϕ |
α |
ϕ |
β |
] |
(140) |
||
Ψ = A[ϕ ϕ |
2 |
...ϕn |
i |
j |
||||||||||
|
1 |
|
1 |
|
c |
|
|
|
|
|
||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ψ |
|
ˆ |
2 |
|
2 |
2 |
ϕ |
α |
ϕ |
β |
] |
(141) |
||
2 |
= A[ϕ ϕ |
2 |
...ϕn |
j |
i |
|||||||||
|
|
1 |
|
c |
|
|
|
|
|
|||||
94
и верхний знак в (139) соответствует синглету, а нижний – триплету. Вычислить необходимо
|
|
1,3 |
E = |
1 |
ˆ |
± Ψ2 , |
(142) |
|
|
|
|
2 |
Ψ1 ± Ψ2 | H | Ψ1 |
||||
где Ψ1 |
| H | Ψ1 = Ψ2 |
| H | Ψ2 |
есть энергии на однодетерминантных волновых |
|||||
|
ˆ |
ˆ |
|
|
|
|
|
|
функциях Ψ1 и Ψ2 , вычисляются которые по общей формуле (87) подстановкой
na = nb = nc +1, ap = bp =ϕp ( p ≤ nc ), anc +1 =ϕi иbnc +1 =ϕj ,
так что в итоге имеем:
ˆ |
nc |
|
nc |
nc |
|
|
|
∑2hpp + hii + hjj |
+ ∑ (2J pq − Kpq ) + ∑[2(J pi + J pj ) − (Kpi + Kpj )]+ Jij .(143) |
||||||
Ψ1 | H | Ψ1 = |
|||||||
|
p=1 |
|
p,q=1 |
p=1 |
|
|
|
В предположении вещественности орбиталей |
|
|
|||||
|
|
|
ˆ |
ˆ |
|
(144) |
|
|
|
Ψ1 | H | Ψ2 |
= Ψ2 | H | Ψ1 = Kij . |
|
|||
Для упрощения окончательной формулы переобозначим i = nc +1, j = nc + 2 , |
|||||||
Тогда |
|
|
|
|
|
|
|
nc |
|
nc +2 |
nc |
nc nc +2 |
|
|
|
1,3 E = ∑2hpp + |
∑ hqq + |
∑ (2J pq − Kpq ) + ∑ ∑ (2J pq − Kpq ) + Jij ± K ji . (145) |
|||||
p=1 |
|
q=nc +1 |
p,q=1 |
p=1q=nc +1 |
|
|
|
В итоге получились следующие значения коэффициентов – |
|
||||||
общие значения: ωc = 2, ωo |
=1, αcc = 2, αco = αoc =1, αoo =1/ 2, |
βcc =1, |
βco =1/ 2; |
||||
частные значения: для синглета βoo |
= −1/ 2 , а для триплета βoo |
=1/ 2 . |
|
||||
Также констатируем, что компоненты триплета с Sz =1 и Sz = 0 имеют одну |
|||||||
и ту же энергию при том, что |
компонента триплета с |
Sz =1 |
описывается |
||||
однодетерминантной волновой функцией, а компонента с |
Sz = 0 |
– линейной |
|||||
комбинацией двух детерминантов. |
|
|
|
||||
Литература
1.D. R. Hartree. The Wave Mechanics of an Atom with a Non-Coulomb Central Field. Part I. Theory and Methods, Proc. Cambridge Phil. Soc., v. 24: 1, 89 – 110 (1928).
2.D. R. Hartree. The Wave Mechanics of an Atom with a Non-Coulomb Central Field.
Part II. Some Results and Discussion, Proc. Cambridge Phil. Soc., v. 24: 1, 111 – 132 (1928).
3.V. A. Fock. An approximate method for solving the quantum many-body problem, Z. Physik, v. 61: 1-2, 126 – 148 (1930).
4.D. E. Rutherford. Substitutional Analysis. London: Edinburgh University Press, 1948.
95
5.M. Hammermesh. Group theory and its application to physical problems.
Reading: Addison-Wesley, 1962.
6.И. Г. Каплан. Симметрия многоэлектронных систем. Москва: Наука, 1969.
7.W. A. Goddard III. Improved quantum theory of many-electron systems: I. Construction of eigenfunctions of Sˆ2 which satisfy Pauli's principle, Phys. Rev., v. 157: 1, 73 – 80 (1967).
8.W. A. Goddard III. Improved quantum theory of many-electron systems:
II.The basic method, Phys. Rev., v. 157: 1, 81 – 93 (1967).
9.W. A. Goddard III. Improved quantum theory of many-electron systems: III. The GF method,
J.Chem. Phys., v. 48: 1, 450 – 461 (1968).
10.W. A. Goddard III. Wavefunctions and correlation energies for two-, three-, and four-electron atoms, J. Chem. Phys., v. 48: 3, 1008 – 1017 (1968).
11.W. A. Goddard III. Improved quantum theory of many-electron systems:
IV. Properties of GF wavefunctions, J. Chem. Phys., v. 48: 12, 5337 – 5347 (1968).
12.R. C. Ladner, W. A. Goddard III. Improved quantum theory of many-electron systems:
V.The spin-coupling optimized GI method, J. Chem. Phys., v. 51: 3, 1073 – 1087 (1969).
13.W. A. Goddard III. The symmetric group and the spin generalized SCF method, Intern. J. Quantum Chem., v. IIIS, 593 – 600 (1970).
14.J. C. Slater. The theory of complex spectra, Phys. Rev., v. 34, 1293 – 1323 (1929).
15.J. C. Slater. Quantum theory of molecules and solids, Phys. Rev., v. 35: 2, 210 – 211 (1930).
16.C. C. J. Roothaan. New developments in molecular orbital theory,
Rev. Modern Phys., v. 23, 69 (1951).
17.A. T. Amos, G. G. Hall. Single determinant wave functions, Proc. Royal Soc., v. A263: 1315, 483 – 493 (1961).
18.И. И. Украинский, Ю. А. Кругляк, Х. Прейсс, Р. Яношек. Проектирование волновой функции неограниченного метода Хартри – Фока на дублетное состояние на примере бензильного радикала, Теор. экспер. химия, т. 8: 3, 299 – 308 (1971).
19.A. T. Amos. Some properties of π-ions and triplets,
In O. Sinanoğlu (ed.), Modern quantum chemistry. New York: Academic Press, 1965.
20.И. И. Украинский, Ю. А. Кругляк. Обобщенный метод Хартри – Фока и его применение к расчету электронных оболочек атомов, молекул и полимеров,
В сб. Г. Ф. Филиппов (ред.), Современные проблемы оптики и ядерной физики.
Киев: Наукова думка, 1974.
21.J. A. Pople, R. K. Nesbet. Self-consistent orbitals for radicals,
J.Chem. Phys., v. 22: 3, 571 – 572 (1954).
22.P.-O. Lowdin. Quantum theory of many-particle systems. III. Extension of
the Hartree – Fock scheme to include degenerate systems and correlation effects, Phys. Rev., v. 97: 6, 1509 – 1520 (1955).
23. P.-O. Lowdin. Correlation problem in many-electron quantum mechanics. I. Review of different approaches and discussion of some current ideas,
In I. Prigogine (ed.), Adv. Chem. Phys., v. 2. New York: Interscience, 1959.
24.P.-O. Lowdin. Angular momentum wave functions constructed by projection operators, Rev. Modern Phys., v. 36: 4, 966 – 976 (1964).
25.F. Sasaki, K. Ohno. Spin-component analysis of single-determinant wavefunctions,
J.Math. Phys., v. 4: 9, 1140 – 1147 (1963).
26.V. H. Smith. Projection of exact spin eigenfunctions, J. Chem. Phys., v. 41: 1, 277 (1964).
27.K. M. Sando, J. E. Harriman. Spin-projected and extended SCF calculations,
J.Chem. Phys., v. 47, 180 (1967).
28.F. Harris. On the calculation of spin densities, J. Molec. Phys., v. 11, 243 – 256 (1966).
29.R. Pauncz. Alternant Molecular Orbital Method. London: W. B. Saunders, 1967.
30.P.-O. Lowdin. Band theory, valence band and tight-binding calculations,
J.App. Phys. Suppl., v. 33: 1, 251 – 280 (1962).
96
31.R. Pauncz, J. de Heer, P.-O. Lowdin. Studies of the alternant molecular orbital method.
I.General energy expression for an alternant system with closed-shell structure,
J.Chem. Phys., v. 36, 2247 – 2256 (1962).
32.R. Pauncz, J. de Heer, P.-O. Lowdin. Studies of the alternant molecular orbital method.
II.Application to Cyclic Systems, J. Chem. Phys., v. 36, 2257 – 2265 (1962).
33.E. Hückel. Zur Quantentheorie der Doppelbindung, Z. Phys., v. 60: 7 – 8, 423 – 456 (1930).
34.E. Hückel. Quantentheoretische Beiträge zum Benzolproblem,
Z.Phys., v. 70: 3 – 4, 204 – 286 (1931).
35.Ю. А. Кругляк et al. Методы вычислений в квантовой химии. Расчет π-электронной структуры молекул простыми методами молекулярных орбиталей.
Киев: Наукова думка, 1967.
36.C. A. Coulson, H. C. Longuet-Higgins. The electronic structure of conjugated systems.
I.General theory, Proc. Roy. Soc., v. A191, 39 – 60 (1947).
37.A. Brickstock, J. A. Pople. Resonance energies and charge distributions of unsaturated hydrocarbon radicals and ions, Trans. Faraday Soc., v. 50, 901 – 911 (1954).
38.T. A. Koopmans. Über die zuordnung von wellenfunktionen und eigenwerten zu den einzelnen elektronen eines atoms, Physica, v. 1, 104 – 113 (1933).
39.L. Brillouin. La méthode du champ self-consistent, Actual. Scient. Industr., n. 71. Paris: Hermann, 1933.
40.L. Brillouin. Les champs "self-consistents" de Hartree et de Fock, Actual. Scient. Industr., n. 159. Paris: Hermann, 1934.
41.Е. В. Моздор, Ю. А. Кругляк, В. А. Куприевич. Матричные элементы операторов физических величин на одноконфигурационных функциях радикалов,
Теор. экспер. химия, т. 5: 6, 723 – 730 (1969).
42.Yu. A. Kruglyak, E. V. Mozdor, V. A. Kuprievich. Study of the electronic structure of radicals by the CI method. I. Matrix elements of the physical value operators,
Croat. Chem. Acta, v. 43, 15 – 22 (1971).
43.N. A. Popov. Symmetry properties of one-electron orbitals in the method of different orbitals for different spins, J. Struct. Chem,, v. 11: 4, 670 – 676 (1970).
44.E. A. Hylleraas. Neue berechnung der energie des Heliums im grundzustande, sowie des tiefsten terms von ortho-helium, Z. Phys., v. 54, 347 – 366 (1929).
45.C. Ekkart. The theory and calculation of screening constants,
Phys. Rev., v. 36, 878 – 892 (1930).
46.H. Shull, P.-O. Lowdin. Superposition of configurations and natural spin orbitals. Applications to the He problem, J. Chem. Phys., v. 30, 617 – 626 (1959).
47.D. P. Chong. Different orbitals for different spins. Singlet ground state of Helium, J. Chem. Phys., v. 45, 3317 – 3318 (1966).
48.L. Green, M. Lewis, M. Mulder et al. Correlation energies and angular components of the
wave functions of the ground states of H–, He, and Li+, Phys. Rev., v. 93, 273 (1954).
49.R. A. Bonham, D. A. Kohl. Simple correlated wavefunctions for the ground state of Helium-like atoms, J. Chem. Phys., v. 45, 2471 (1966).
50.М. Д. Долгушин. Расщепленные орбитали и энергии корреляции основного состояния двухэлектронных атомов,
В сб. A. Юцис (ред.), Теория электронных оболочек атомов и молекул.
Вильнюс: Минтис, 1971.
51.S. Fraga, B. J. Ransil. Studies in molecular structure. VI. Potential curve for the interaction of two hydrogen atoms in the LCAO MO SCF approximation,
J. Chem. Phys., v. 35, 2471 (1967).
52.W. Kolos, L. Wolniewicz. Accurate adiabatic treatment of the ground state of the hydrogen molecule, J. Chem. Phys., v. 41, 3663 (1964).
53.J. D. Swalen, J. de Heer. Many parameter alternant molecular orbital calculations for large cyclic systems with closed shell structure, J. Chem. Phys., v. 40, 378 (1964).
97
54.G. G. Hall, A. T. Amos. Molecular orbital theory of the spin properties of conjugated molecules,
In D. R. Bates and I. Estermann (eds), Adv. Atomic Molec. Phys., v. 1, 1 – 59 (1965).
55.J. A. Pople, D. L. Beveridge, P. A. Dobosh. Molecular orbital theory of the electronic structure of organic compounds. II. Spin densities in paramagnetic species,
J.Amer. Chem. Soc., v. 90, 4201 (1968).
56.Ю. А. Кругляк, Х. Прейсс, Р. Яношек. Неэмпирический расчет электронной структуры бензильного радикала, Укр. физ. ж., т. 15: 6, 980 – 988 (1970).
57.Ю. А. Кругляк, Х. Прейсс, Р. Яношек. Расчет электронных оболочек бензильного радикала неограниченным методом Хартри – Фока на гауссовом базисе,
Ж. структ. химии, т. 12: 4, 689 – 696 (1971).
58.Ю. А. Кругляк, И. И. Украинский, Х. Прейсс, Р. Яношек. Орбитальный анализ ab initio электронной и спиновой заселенности атомов бензильного радикала,
Теор. экспер. химия, т. 7: 6, 815 – 819 (1970).
59.A. Carrington, I. C. P. Smith. The electron spin resonance spectrum and spin density distribution of the benzyl radical, Molec. Phys., v. 9: 2, 137 – 147 (1965).
60.H. G. Benson, A. Hudson. On the spin density distribution in the benzyl radical, Molec. Phys., v. 20: 1, 185 – 187 (1971).
61.R. V. Lloyd, D. E. Wood. Free radicals in adamantane matrix. EPR and Indo study of the benzyl, aniline, and phenoxy radicals and their fluorinated derivatives,
J.Amer. Chem. Soc., v. 96: 3, 659 – 665 (1974).
62.H. M. McConnell. Electron densities in semiquinones by paramagnetic resonance, J. Chem. Phys., v. 24: 3, 632 (1956).
63.H. M. McConnell. Indirect hyperfine interactions in the paramagnetic resonance spectra of aromatic free radicals, J. Chem. Phys., v. 24: 4, 764 (1956).
64.R. W. Fessenden, R. H. Schuler. Electron spin resonance studies of transient alkyl radicals,
J.Chem. Phys., v. 39: 9, 2147 (1963).
65.Ю. А. Кругляк, E. В. Моздор, В. A. Куприевич. Полное конфигурационное взаимодействие для бензильного радикала, Укр. физ. ж., т. 15: 1, 48 – 58 (1970).
66.Ю. А. Кругляк, Г. Хибаум, Н. E. Радомысельская. Электронная структура основного состояния бензильного радикала в равновесной конфигурации,
Rev. Roumaine Chim., v. 17: 5, 781 – 799 (1972).
67.Yu. A. Kruglyak, E.V.Mozdor. Study of the electronic structure of radicals by the CI method. 3. Excited states of the benzyl radical, Theor. chim. Acta, v. 15, 374 – 384 (1969).
68.Yu. A. Kruglyak, I. I. Ukrainsky. Study of the electronic structure of alternant radicals by the DODS method, Intern. J. Quantum Chem., v. 4, 57 – 72 (1970).
69.I. I. Ukrainsky. Electronic structure of long cumulene chains,
Intern. J. Quantum Chem., v. 6: 3, 473 – 489 (1972).
70.Ю. А. Кругляк, И. И. Украинский. О расчете спиновой плотности в методе расщепленных орбиталей,
Bсб. A. Юцис (ред.), Теория электронных оболочек атомов и молекул.
Вильнюс: Минтис, 1971.
71.A. A. Овчинников, И. И. Украинский, Г. Ф. Квенцель. Теория одномерных мотовских полупроводников и электронная структура длинных молекул с сопряженными связями,
Усп. физ. наук, т. 108: 1, 81 – 111 (1972).
72.И. A. Мисуркин, A. A. Овчинников. Электронная структура длинных молекул с сопряженными связями, Теор. экспер. хим., т. 3: 4, 431 – 436 (1967).
73.K.-F. Berggren, B. Johansson. A field theoretical description of states with different orbitals for different spins, Intern. J. Quantum Chem., v. 2: 4, 483 – 508 (1968).
74.B. Johansson, K. F. Berggren. Itinerant Antiferromagnetism in an Infinite Linear Chain, Phys. Rev., v. 181, 855 (1969).
98
75.H. Fukutome. Spin density wave and charge transfer wave in long conjugated molecules, Prog. Theor. Phys., v. 40: 5, 998 (1968).
76.H. Fukutome. Spin density wave and charge transfer. Wave in long conjugated molecules, Prog. Theor. Phys., v. 40: 6, 1227 – 1245 (1968).
77.И. A. Мисуркин, A. A. Овчинников. Электронная структура больших π-электронных систем (графит, полиацены, кумулены), Теор. эксп. хим., т. 4: 1, 3 – 11 (1968).
78.I. A. Misurkin, A. A. Ovchinnikov. Electronic structure of large π-electron systems (graphite, polyacenes, cumulenes), Theor. chim. Acta, v. 13, 115 – 124 (1969).
79.I. I. Ukrainsky, G. F. Kventsel. Electronic structure of long polyene chains with an impurity atom, Theor. chim. Acta, v. 25, 360 – 371 (1972).
80.E. H. Lieb, F. Y. Wu. Absence of Mott transition in an exact solution of the short-range, one-band model in one dimension, Phys. Rev. Lett., v. 20, 1445 – 1448 (1968).
81.Yu. A. Kruglyak. Quantum-chemical Studies of Quasi-one-dimensional Electron Systems.
1.Polyenes, ScienceRise, v. 5: 2(10), 69 – 105 (2015).
82.Yu. A. Kruglyak. Quantum-chemical Studies of Quasi-one-dimensional Electron Systems.
2.Cumulenes and Origin of Forbidden Zone, ScienceRise, v. 6: 2(11), 70 – 100 (2015).
83.Yu. A. Kruglyak. Quantum-mechanical Studies of Quasi-One-Dimensional Electron Systems, Chapter 2 in book Yu. A. Kruglyak et al. Calculational Methods in Quantum Geometry and Chaos Theory, Part 4, 28 – 180 (2015). Odessa: TES Publishing House, 2015.
84.Istvan Mayer. Simple theorems, proofs, and derivations in quantum chemistry. New York: Kluwer Academic, 2003.
85.I. Mayer. Spin-projected EHF Method. IV. Comparison of Potential Curves Given by Different One-electron Methods, Intern. J. Quantum Chem., v. 14, 29 – 38 (1978).
86.G. G. Hall. The molecular orbital theory of chemical valency. VIII. A Method of calculating ionization potentials, Proc. Roy. Soc., v. A205, 541 – 552 (1951).
87.Ю. О. Кругляк. Деякі методологічні питання та перспективи розвитку квантової хімії,
Вісник АН УРСР, № 7, 32 – 46 (1972).
2.6.Корреляция электронов
Метод ХФ учитывает взаимодействие между электронами усредненным образом, а хартри-фоковские волновые функции далеки от точных решений молекулярного уравнения Шредингера. Они не учитывают то обстоятельство, что движение электронов скоррелировано, что электроны не движутся независимо друг от друга. Фактически волновая функция должна зависеть от межэлектронных расстояний.
Представить это себе можно так. Если p1(r1) есть плотность вероятности найти электрон № 1 в точке r1 независимо от положения остальных электронов, а для электрона № 2 такая плотность вероятности равна p2 (r2 ) , то для плотности вероятности p12 (r1,r2 ) того, что электрон № 1 будет найден в точке r1 и
одновременно электрон № 2 будет найден в точке |
r2 , должно иметь место |
неравенство |
|
p12(r1,r2 ) ≠ p1(r1) p2(r2 ) , |
(146) |
как очевидное для статистически зависимых событий.
Движение ансамбля электронов совершенно независимо друг от друга реализуется только в приближении Хартри, когда волновая функция берется в
99
