
Yuriy Kruglyak. Quantum Chemistry_Kiev_1963-1991
.pdfВыражения в квадратных скобках можно упростить, избавившись от ограничения j ≠ i при суммировании. Действительно, поскольку
ˆa |
|
|
|
ˆ a |
ai , |
(80) |
|
Ji |
|
ai = Ki |
|||||
ˆb |
|
|
ˆ b |
bi , |
(81) |
||
Ji |
|
bi = Ki |
|||||
то слагаемые самоотталкивания |
|
|
|
|
|
|
|
ˆa |
|
|
ˆ a |
)ai = 0, |
(82) |
||
(Ji |
− Ki |
||||||
ˆb |
|
|
ˆ b |
)bi = 0 |
(83) |
||
(Ji |
|
− Ki |
|
||||
можно добавить в выражения в квадратных скобках уравнений (78) и (79). В результате операторы в квадратных скобках становятся одними и теми же для всех орбиталей. Эти операторы Фока
ˆ a |
ˆ |
na |
ˆa |
ˆ a |
nb |
ˆb |
, |
|
F |
= h |
+∑(J j |
− K j |
)+∑J j |
||||
|
|
j=1 |
|
|
j=1 |
|
(84) |
|
ˆ b |
ˆ |
nb |
ˆb |
ˆ b |
na |
ˆa |
||
|
||||||||
F |
= h +∑(J j |
− K j |
)+∑J j |
|
||||
|
|
j=1 |
|
|
j=1 |
|
|
|
еще называют фокианами и уравнения метода НХФ записываются более компактно, а именно:
ˆ a |
na |
a |
(i =1,2,3,...,na ) |
F |
ai = ∑ε ji a j , |
||
|
j=1 |
|
|
ˆ b |
nb |
b |
(i =1,2,3,...,nb ) |
|
|||
F |
bi = ∑ε ji bj. |
||
|
j=1 |
|
|
(78) и (79) с ними
(85)
Фокианы Fˆ a и Fˆ b зависят от всех орбиталей, заселенных электронами с обеими проекциями спина в функции Ψ (73), но зависимость эта специфичная
– такова, что фокианы определяются двумя подпространствами, растянутыми наборами лишь занятых орбиталей {ai} и {bi}. Дело в том, что фокианы Fˆ a и Fˆ b
инвариантны относительно унитарных преобразований орбиталей, заселенных электронами с той же самой проекцией спина [84].
Величины εaji и εbji в (85) есть элементы эрмитовых матриц εa и εb размера na ×na и nb ×nb , соответственно, так что фокианы также эрмитовы. Эти матрицы
есть матрицы операторов Фока Fˆ a и Fˆ b в подпространстве занятых орбиталей {ai} и {bi} и они могут быть диагонализованы, так что вместо (85) имеем уравнения метода НХФ в каноническом виде
ˆ a |
a |
ai , |
(i =1,2,3,...,na ) |
|
|
F |
ai =εi |
(86) |
|||
ˆ b |
b |
bi. |
(i =1,2,3,...,nb ) |
||
|
|||||
F |
bi =εi |
|
80
В итоге мы имеем систему двух зацепляющихся задач на псевдособственные значения εia и εib , называемые обычно орбитальными
энергиями, поскольку они похожи на энергии одноэлектронной системы во внешнем поле, и эта связь выражается теоремой Купманса [38].
2.3.1. Теорема Купманса
Сначала выпишем выражение для энергии в методе НХФ для ортонормированных орбиталей комбинируя (67) и (82) и используя обозначение (68) для интегралов, а именно:
|
|
|
na |
ˆ |
nb |
ˆ |
1 na |
|
|
|
E = ∑ ai|h |ai + ∑ bi|h |bi + |
∑([aia j |aia j ] −[aia j |a jai ]) + |
|
||||||||
|
|
|
i=1 |
i=1 |
|
2 i, j |
=1 |
|
(87) |
|
|
|
|
|
nb |
|
|
|
na |
nb |
|
|
|
|
|
|
|
|
|
|||
|
|
+ |
1 ∑([bibj |bibj ] −[bibj |bjbi ]) +∑∑[aibj |aibj ]. |
|
||||||
|
|
|
2 i |
, j=1 |
|
|
|
i=1 |
j=1 |
|
Это выражение для энергии EN |
системы с N = na + nb электронами. Перепишем |
|||||||||
его, выделив слагаемые, содержащие орбиталь ak , а именно: |
|
|||||||||
|
na |
|
ˆ |
ˆ |
nb |
ˆ |
|
|
|
|
EN = ∑ |
ai|h |ai + ak |h |ak +∑ bi|h |bi + |
|
||||||||
|
i=1 |
|
|
|
i=1 |
|
|
|
|
|
|
(i |
≠k ) |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
n |
|
|
|
+ |
1 |
∑a |
([aia j |aia j ] −[aia j |a jai ]) + |
1 ∑a ([aka j |aka j ] −[aka j |a jak ]) + |
|
|||||
|
2 |
i, j=1 |
|
|
|
|
2 j=1 |
(88) |
||
|
|
(i, j≠k ) |
|
|
|
n |
|
|||
|
1 |
n |
|
|
|
|
+ 1 |
|
|
|
+ |
∑a ([aiak |aiak ] −[aiak |akai ]) |
∑a ([bibj |bibj ] −[bibj |bjbi ]) + |
|
|||||||
|
2 i=1 |
|
|
|
2 j=1 |
|
|
|||
|
n |
n |
|
n |
|
|
|
|
|
|
+ ∑a |
∑b [aibj |
|aibj ]+∑b ([akbj |akbj ]. |
|
|
||||||
|
i=1 |
j=1 |
j=1 |
|
|
|
|
|
||
|
(i≠k ) |
|
|
|
|
|
|
|
|
|
Вычленим слагаемые, не содержащие ak . Они в точности соответствуют энергии EN −1(ak ) N −1-электронной системы с волновой функцией, получаемой из (73) удалением орбитали ak . Воспользовавшись тождествами типа
[ab |cd] ≡[ba |d c], |
[aka j |aka j ] ≡ ak |
ˆa |
|
ˆ a |
|ak , (89) |
|||
| J j |ak , [aka j |a jak ] ≡ ak | K j |
||||||||
преобразуем слагаемые в (88), содержащие ak , и получим |
|
|
|
|||||
ˆ |
|
na |
ˆa |
ˆ a |
nb |
ˆb |
|
|
|
|
|
|
|
||||
EN = EN −1(ak ) + ak |h |
|ak +∑( ak | J j |
|ak − ak | K j |
|ak ) + ∑ ak | J j |ak = |
(90) |
||||
|
|
j=1 |
|
|
j=1 |
|
|
|
|
ˆ a |
|
|
a |
|
|
|
|
= EN −1(ak ) + ak | F |
|ak = EN −1(ak ) +εk , |
|
|
|
|
|||
81
что и дает нам теорему Купманса |
|
|
|
|
|
|
E |
N |
= E |
N −1 |
(a ) +εa . |
(91) |
|
|
|
k |
k |
|
||
Итак, диагональные элементы матриц εa |
и εb |
равны изменению энергии |
||||
системы при удалении электрона с некоторой орбитали при сохранении остальных занятых орбиталей в неизменном виде. Обычно энергии εka(b)
отрицательны и называются вертикальными потенциалами ионизации, т. е. вычисленными без учета изменения геометрии атомных ядер системы, которое сопровождается орбитальной релаксацией.
Важно иметь в виду, что сумма всех орбитальных энергий системы, рассчитанной при неизменной геометрии ядер, не равна полной электронной энергии этой системы. Орбитальная энергия εka учитывает полную энергию
взаимодействия электрона, находящегося на орбитали ak , со всеми остальными электронами, тогда как энергия EN −1(ak ) не содержит никаких слагаемых, связанных с орбиталью ak . При простом суммировании орбитальных энергий энергия электрон-электронного взаимодействия Eee учитывается дважды, тогда
как кинетическая энергия и энергия электрон-ядерного притяжения учитывается только один раз:
n |
n |
|
E = ∑a |
εia +∑b εib − Eee . |
(92) |
i=1 |
i=1 |
|
Можно поступить иначе: вместо вычитания Eee из суммы орбитальных энергий
добавим еще раз одноэлектронную часть энергии и разделим результат пополам, а именно:
E = |
1 |
na |
(ε |
a |
+ a |
ˆ |
|a |
) + |
nb |
(ε |
b |
+ b |
ˆ |
|b |
|
= |
1 |
na |
a |
ˆ a |
ˆ |
|a |
+ |
nb |
b |
ˆ b |
ˆ |
|b |
|
.(93) |
|
|
|
∑ |
i |
| h |
∑ |
i |
| h |
) |
|
|
| F |
+ h |
∑ |
| F |
+ h |
|
|||||||||||||||
|
2 |
|
|
i |
|
i |
|
|
i |
|
i |
|
|
2 |
∑ |
i |
|
|
i |
|
i |
|
|
i |
|
|
|||||
|
i=1 |
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
i=1 |
|
|
|
|
|
i=1 |
|
|
|
|
|
|
||||
Занятые орбитали обычно характеризуются наинизшими орбитальными энергиями. В расчетах нейтральных систем орбитальная энергия высшей заполненной молекулярной орбитали (ВЗМО) обычно отрицательная, а низшей вакантной молекулярной орбитали (НВМО) – положительная. Это связано с тем, что к операторам Фока добавлены слагаемые самоотталкивания (82) и (83), чтобы привести их к виду (84), единому для всех орбиталей. Однако, при
действии фокианов на |
виртуальную орбиталь avj |
они содержат отличные от |
||
нуля слагаемые вида |
(Ji |
− Ki |
)a j ≠ 0. Электрон, |
заселяющий виртуальную |
|
ˆa |
ˆ a |
v |
|
орбиталь, как бы видит на один электрон больше, чем электрон на занятой орбитали, и это выталкивает наверх энергии виртуальных орбиталей. Другими
82
словами, включение самоотталкивания в операторы Фока приводит к тому, что энергии виртуальных орбиталей учитывают взаимодействие еще с одним электроном. Поэтому виртуальные орбитали ближе к состояниям отрицательного иона, а не к возбужденным состояниям исходной нейтральной системы. Энергии виртуальных состояний связывают со сродством системы к электрону. Как правило, нельзя получить надежное описание связанных состояний отрицательных молекулярных ионов без учета орбитальной релаксации в результате оптимизации геометрии ядер в системе и без явного учета электронной корреляции.
2.4. Ограниченный метод Хартри – Фока и его развитие
Для расчета синглетных состояний молекул с замкнутой электронной оболочкой обычно используется ограниченный метод ХФ (ОХФ/RHF). В этом случае N = 2n с одинаковым числом n спинов α и β . Однодетерминантная волновая функция такова:
ˆ |
(1)ϕ1(2)β(2)ϕ2(3)α(3)ϕ2 |
(4)β(4) ...ϕn (2n −1)α(2n −1)ϕn (2n)β(2n)].(94) |
|||||||
Ψ = A[ϕ1(1)α |
|||||||||
Уравнения метода ОХФ получаются из канонических уравнений НХФ |
|||||||||
(86) заменой |
|
|
|
|
|
|
|
|
|
|
a = b =ϕ |
, |
n |
= n |
|
= n, |
εa |
=εb =ε,... , |
(95) |
|
i i i |
|
a |
b |
|
i |
i |
|
|
так что |
|
|
|
|
|
|
|
|
|
|
ˆ |
|
=εiϕi , |
(i =1,2,3,...,n) |
(96) |
||||
|
Fϕi |
||||||||
а фокиан |
|
|
|
|
|
|
|
|
|
|
|
ˆ |
ˆ |
n |
|
ˆ |
ˆ |
|
(97) |
|
|
|
|
|
|||||
|
F = h |
+∑(2J j |
− K j ). |
||||||
|
|
|
|
j=1 |
|
|
|
|
|
В области равновесных геометрий молекул с замкнутыми оболочками решение НХФ нередко совпадает с решением ОХФ. Это означает, что волновая функция ОХФ обеспечивает минимум энергии среди всех однодетерминантных волновых функций. Обратная ситуация может наблюдаться при больших межатомных расстояниях вдали от равновесия. В этом случае решение НХФ дает меньшую энергию, чем решение ОХФ, являющимся лишь седловой точкой.
Волновая функция (94) метода ОХФ для замкнутой оболочки, построенной из дважды заселенных орбиталей, является чистым синглетом, т. е. собственной
функцией операторов |
ˆ ˆ ˆ |
и как следствие этого также и оператора |
ˆ2 |
с |
Sx , Sy , Sz |
S |
собственными значениями, равными нулю. В случае же метода НХФ, называемого также методом разных орбиталей для разных спинов (РОРС)
83
однодетерминантная волновая функция является собственной функцией оператора Sˆz , но не оператора Sˆ2 . Это означает, что функции НХФ нельзя
приписать определенную спиновую мультиплетность, и такая функция есть смесь синглетных, триплетных и более высоких по суммарному спину компонент.
Как уже упоминалось ранее (§ 2.1), чтобы избавиться от спинового загрязнения Лёвдин ввел оператор спинового проектирования (СП/SP)
ˆ S |
|
ˆ2 |
−l(l +1) |
|
|
|||
= ∏ |
S |
|
|
|
||||
O |
|
|
|
|
, |
(98) |
||
S(S |
+1) |
−l(l +1) |
||||||
|
l≠S |
|
|
|||||
который позволяет получить чистую спиновую компоненту из волновой функции НХФ, принадлежащую нужному собственному значению оператора Sˆ2 . Этот оператор уничтожает все нежелательные спиновые компоненты, оставляя неизменной только искомую. Действительно, любую волновую
функцию Ψ |
|
можно |
представить в |
виде суммы |
|
Ψ = ∑l Ψ |
|
слагаемых |
l Ψ с |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
разными спиновыми мультиплетностями 2l +1. В операторе |
ˆ S |
сомножитель в |
||||||||||||||||
O |
|
|||||||||||||||||
ˆ2 |
− l(l +1) |
уничтожает компоненту |
l |
Ψ: |
|
|
|
|
|
|
|
|||||||
числителе S |
|
|
|
|
|
|
|
|
||||||||||
ˆ2 |
−l(l +1)] |
l |
ˆ2 l |
Ψ −l(l |
+1) |
l |
Ψ = l(l +1) |
l |
Ψ −l(l +1) |
l |
Ψ = 0. |
(99) |
||||||
[S |
|
|
Ψ = S |
|
|
|
||||||||||||
В результате действия произведения таких сомножителей все компоненты l Ψ с
l ≠ S уничтожаются. Если же оператор S |
− l(l +1) действует на слагаемое |
|
Ψ с |
|||||||||||
|
|
|
|
|
ˆ2 |
|
|
|
|
|
|
|
S |
|
нужной мультиплетностью 2S +1, то имеем: |
|
|
|
|
|
|
|
|||||||
ˆ2 |
−l(l +1)] |
S |
ˆ2 S |
Ψ −l(l +1) |
S |
Ψ = S(S +1) −l(l +1) |
S |
Ψ . |
|
(100) |
||||
[S |
|
Ψ = S |
|
|
|
|||||||||
Коэффициент |
S(S +1) − l(l +1) перед |
S Ψ в |
|
правой части |
(100) |
уничтожается |
||||||||
знаменателем в (98). В |
результате |
действия оператора |
O |
|
на |
«грязную» |
||||||||
|
|
|
|
|
|
|
|
|
ˆ S |
|
|
|
|
|
волновую функцию НХФ уничтожаются все компоненты l Ψ кроме нужной компоненты S Ψ.
Хорошей иллюстрацией, демонстрирующей характерное поведение потенциальных кривых, полученных разными вариантами обобщенного метода ХФ, может служить рис. 2.
Метод ОХФ/RHF предсказывает равновесное межатомное расстояние с вполне приемлемой точностью, но переоценивает кривизну в минимуме энергии примерно на 15 – 20 %. Колебательные частоты в такой ситуации корректируются в сторону уменьшения. При бóльших межатомных
84
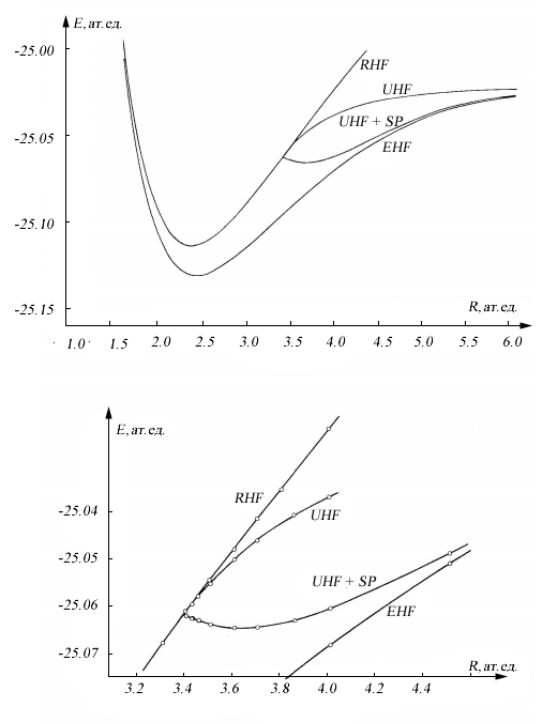
расстояниях потенциальная кривая ОХФ резко возрастает и имеет неправильную асимптотику из-за наличия ионных вкладов.
Рис. 2. Потенциальные кривые молекулы BH, полученные разными вариантами обобщенного метода ХФ [85].
Как и в этом расчете [85], стандартный метод НХФ/UHF не приводит к решению, отличному от ОХФ как при равновесном расстоянии, так и при несколько бóльших расстояниях, а в этом расчете вплоть до R ≈ 3.4 ат.ед. В этой области на потенциальной кривой есть точка бифуркации, в которой возникает нетривиальное новое решение НХФ, и потенциальная кривая НХФ плавно
85
отходит от кривой ОХФ. В этой точке бифуркации решения ОХФ и НХФ совпадают [85]. Далее кривая НХФ стремится к качественно правильному диссоциационному пределу. Заметим только, что она приближается к асимптотическому значению энергии слишком быстро, если сравнивать ее поведение с ходом асимптотики в расширенном методе ХФ (РХФ/EHF).
Волновая функция в результате спинового проектирования исходного детерминанта НХФ (НХФ-СП/UHF-SP) уже не является однодетерминантной. В результате спинового проектирования получается не только чистая спиновая функция, но и как правило наблюдается понижение энергии системы по сравнению с энергией НХФ, как это имеет место в рассматриваемом примере (рис. 2: кривая UHF-SP: область R > 3.4 ат. ед.) Это происходит только в тех областях потенциальной энергии, где реализуются настоящие решения НХФ (рис. 2: кривая UHF после R > 3.4 ат. ед.), отличающиеся от решений НХФ-СП, соответствующих чистому синглету (рис. 2: кривая UHF-SP после R > 3.4 ат. ед.). Причиной такого поведения является то, что вариационным путем оптимизируется не чистая по спину компонента волновой функции, полученная спиновым проектированием, а однодетерминантная волновая функция, которая была у нас перед этим (метод НХФ с последующей спиновой проекцией).
Более последовательным было бы варьирование самого спинспроектированного детерминанта в качестве вариационной пробной волновой функции (варьирование после проектирования). Эта процедура приводит к спин-спроектированному расширенному методу ХФ (РХФ/EHF). Как видим из рис. 2, метод РХФ дает качественно правильное описание гомолитической диссоциации химической связи В–Н.
Важной особенностью спин-спроектированных волновых функций является то обстоятельство, что они хорошо описывают электронную структуру антиферромагнитных систем, представляющих собой совокупность спинов, направленных то вверх, то вниз, и состоящих из двух подрешеток наивысшего возможного спина, которые вместе образуют синглет.
Волновая функция ОХФ есть частное решение уравнений РХФ, однако, в отличие от случая НХФ, решение РХФ с энергией меньше, чем энергия ОХФ, существует всюду (рис. 2). Метод РХФ можно рассматривать как расширенную одноэлектронную модель, поскольку исходный определитель РОРС содержит столько же спин-орбиталей, сколько имеется электронов в системе.
Были предложены упрощенные варианты метода РХФ. Например, используется только один сомножитель в (98), соответствующий наинизшей и, как правило, наибольшей по весу нежелательной спиновой компоненте. В полуспроектированном варианте метода РХФ волновая функция берется в виде суммы или разности лишь двух определителей, отличающихся друг от друга
86
перестановкой всех спин-функций α и β . Такая волновая функция содержит только каждую вторую спиновую компоненту, например, синглет, квинтет и т.д., но не триплет, септет и т.д., и представляет собой почти чистое по спину состояние.
2.5. Метод Хартри – Фока – Рутана
Уравнения Хартри – Фока представляют собой систему связанных интегро-дифференциальных уравнений, которые в случае свободных атомов и простейших молекул решаются численными методами. Применительно к произвольным молекулярным системам решение этих уравнений в виде одноэлектронных орбиталей приходится аппроксимировать конечной линейной комбинацией (ЛК) некоторых заранее выбранных базисных функций (базисных орбиталей). Их обычно, но не обязательно, связывают с отдельными атомами в молекуле (атомные орбитали, АО). Отсюда аббревиатура ЛКАО.
Итак, разлагаем одноэлектронные орбитали ϕi по конечному базису {χµ}:
m |
|
ϕi = ∑cµi χµ, (i =1,2,3,...,m) |
(101) |
µ=1 |
|
где коэффициенты cµi каждой молекулярной орбитали (МО) ϕi |
образуют |
вектор-столбец ci . Базисные функции χµ обычно, но совсем не обязательно,
нормированы на единицу. Как правило, они не ортогональны друг к другу, но должны быть линейно независимыми.
При использовании ограниченного базиса интегро-дифференциальные уравнения ХФ сводятся к матричным уравнениям на псевдособственные значения. Они были выведены Рутаном [16] и Холлом [86] независимо друг от друга и получили название уравнений Хартри – Фока – Рутана (ХФР).
Для вывода уравнений ХФР воспользуемся теоремой Бриллюэна (§ 2.2.1) для однодетерминантной волновой функции, а именно:
ˆ |
(102) |
Ψ1(ϕi →ϕi′) | H | Ψ = 0, (i =1,2,3,...,n) |
|
где ϕi′ ортогональна всем n занятым орбиталям |
|
ϕi′|ϕj = 0, ( j =1,2,3,...,n) , |
(103) |
и, как и ϕi , должна представляться в виде разложения по базисным функциям:
m
ϕi′= ∑qµχµ, (104)
µ=1
87
где на коэффициенты разложения qµ накладывается условие ортогональности
(103).
Наиболее общая произвольная орбиталь вида (104), удовлетворяющая условиям ортогональности, строится следующим образом [84].
Рассмотрим оператор проектирования (Приложение П-2) на подпространство занятых орбиталей:
|
ˆ |
m |
|
|
∑|ϕj ϕj |. |
(105) |
|
|
P = |
||
Оператор 1− P |
проектирует на |
j=1 |
дополнение к этому |
ортогональное |
|||
ˆ |
т. е. произвольная функция |
|ϕi′ = (1− P) | ∑pν χν с |
|
подпространству, |
|||
|
|
|
ˆ |
ν
произвольными коэффициентами pν ортогональна ко всем занятым орбиталям. Коэффициенты pν произвольны и независимы друг от друга. Мы можем,
например, предположить, что для каждой вариации только один из коэффициентов отличен от нуля. Необходимо потребовать выполнение теоремы Бриллюэна для каждой функции вида:
|ϕi′ = (1 |
ˆ |
(106) |
− P) | χν . (ν =1,2,3,...,m). |
||
Выражение теоремы Бриллюэна через одноэлектронные орбитали |
||
приводит к равенству: |
|
|
|
ˆ |
(107) |
|
ϕi′| F |ϕi = 0, |
|
где оператор Фока строится из орбиталей, которые можно разложить по данному одноэлектронному базису. Взяв функцию, сопряженную к (106), получаем:
|
† |
ˆ |
† |
= χν |(1 |
ˆ |
(108) |
|
ϕi′|=[|ϕi′] |
=[|(1− P) | χν |
] |
− P) . |
||
Подставим (108) в (107) и используем (105), а именно: |
|
|
||||
χν |(1 |
ˆ ˆ |
ˆ |
|
m |
ˆ |
|
|
|
|
||||
− P)F |ϕi = χν | F |ϕi − χν |
| ∑|ϕj ϕj |F |ϕi = |
|
||||
|
|
|
|
j=1 |
|
(109) |
ˆ |
m |
|
ˆ |
|
m |
|
|
|
|
| ∑|ϕj εiδij = 0, |
|
||
= χν | F |ϕi − χν | ∑|ϕj ε ji = χν | F |ϕi − χν |
|
|||||
|
j=1 |
|
|
|
j=1 |
|
так что |
|
|
|
|
|
|
|
|
ˆ |
|
|ϕi . |
|
(110) |
|
χν | F |ϕi =εi χν |
|
||||
Остается в полученное равенство подставить (101), ввести обозначения
ˆ |
|
|
χν | F | χµ ≡ Fνµ, |
(111) |
|
χν | χµ ≡ Sνµ, |
||
|
88
и мы окончательно получаем уравнения ХФР в развернутом виде
m |
m |
|
|
∑Fνµcµi =εi ∑Sνµcµi |
(i =1,2,3,...,m) |
(112) |
|
µ=1 |
µ=1 |
|
|
или в матричной записи через матрицы m ×m |
|
||
|
Fci =εiSci |
(113) |
|
или через полные матрицы C , столбцами которой являются векторы ci , а именно:
FC = SCε, |
(114) |
|
где матрица ε является диагональной матрицей орбитальных энергий. Если в |
||
матрице C учитываются как занятые, так и виртуальные орбитали, тогда |
||
матрицы C и ε имеют форму m ×m . Если ограничиться учетом только занятых |
||
орбиталей, тогда матрица C имеет прямоугольную форму m ×n , |
а матрица ε |
– |
квадратную форму n ×n . |
|
|
По мере увеличения числа базисных функций энергия рассматриваемой |
||
молекулярной системы приближается к своему ХФ пределу [87]. |
|
|
2.5.1. Матрица плотности |
|
|
Рассмотрим занятые орбитали ϕi (i =1,2,3,...,n) и запишем |
оператор |
P |
|
|
ˆ |
проектирования на занятое подпространство через коэффициенты ЛКАО в
(101):
|
n |
n m |
m |
m n |
|
m |
P = ∑|ϕi ϕi | = ∑∑|cµi χµ ∑cνi χν | = |
∑ ∑cµicνi | χµ χν | = |
∑ Pµν | χµ χν |, (115) |
||||
ˆ |
|
|
|
|
|
|
|
i=1 |
i=1 µ=1 |
ν =1 |
µ,ν =1 i=1 |
|
µ,ν =1 |
где матрица плотности |
|
|
|
|
||
|
|
|
|
n |
|
|
|
|
|
Pµν = ∑cµicνi |
|
(116) |
|
|
|
|
|
i=1 |
|
|
или в матричных обозначениях в виде суммы диадных произведений
n
P = ∑cici† . (117)
i=1
В случае замкнутой оболочки применительно к ОХФ матрицу плотности еще записывают как
n
D = 2P = 2∑cici† . (118)
i=1
89
