Yuriy Kruglyak. Quantum Chemistry_Kiev_1963-1991

виде простого произведения спин-орбиталей и не учитывается антисимметрия электронов как тождественных частиц. Антисимметризация волновой функции исключает возможность обнаружить два электрона с одинаковыми спинами с одной и той же точке пространства. В алгебре определителей такой детерминант автоматически обращается в нуль. С другой стороны волновая функция должна быть непрерывной. С учетом этого обстоятельства можно утверждать, что вероятность того, что два электрона с одним и тем же спином окажутся близко друг к другу мала. Эта характерная особенность распределения электронов получила название фермиевской дырки. Причиной ее появления является антисимметрия волновой функции, и ферми-дырка реализуется даже в системе невзаимодействующих электронов как чисто кинематический эффект.

В методе ХФ нескоррелировано только движение электронов с противоположными спинами. В силу исключительной практической важности классического метода Хартри – Фока корреляционную энергию определяют как разницу между хартри-фоковской энергией электронной системы и ее точным нерелятивистким значением. Согласно этому общепринятому определению, электронная корреляция включает только те эффекты, которые не являются следствием одной лишь антисимметрии и поэтому не учитываются в методе ОХФ. По другому можно сказать так. Под электронной корреляцией понимаются лишь эффекты, возникающие вследствие кулоновского отталкивания между электронами, которое и является причиной возникновения кулоновской дырки. Таким образом, электронная корреляция является динамическим эффектом, не связанным со спином в отличие от фермиевской дырки, являющейся кинематическим эффектом, зависящим от спина.

Иногда пользуются понятиями статической и динамической корреляции электронов, физический смысл которых трудно четко сформулировать. Динамическая корреляция, как прямое следствие кулоновского отталкивания между электронами, преобладает вблизи равновесных конфигураций молекул. Корреляцию считают статической тогда, когда описание с помощью однодетерминантной волновой функции в методе ОХФ, построенной из дважды занятых орбиталей, совершенно не адекватно физической ситуации, например, в случае гомолитической диссоциации.

Во многих случаях констатируют почти постоянное значение энергии корреляции. Если расчет методом ХФР выполнен с достаточно хорошим базисом, то этого бывает достаточно для количественных оценок. Получение более точных результатов, как правило, требует учета электронной корреляции. Есть задачи, которые невозможно исследовать без учета корреляции

100

электронов, например, изучение поверхности потенциальной энергии протекания химической реакции.

Наиболее адекватный учет электронной корреляции достигается введением межэлектронного расстояния rij в волновую функцию. Именно таким

образом получены наиболее точные результаты для легких атомов и для небольших двухатомных молекул. В практических расчетах молекул с учетом корреляции электронов чаще всего пользуются методом конфигурационного взаимодействия, к изложению которого мы переходим.

2.7. Метод конфигурационного взаимодействия

Возьмем нормируемую N-электронную волновую функцию

и фиксируем значения пространственных и спиновых координат её первых N −1

перестановок электронов, что накладывает некоторые ограничения на значения коэффициентов ci1 i2 ...iN , например, из требования антисимметрии относительно

перестановки электронов 1 и 2 следует

и т. д. Если собрать слагаемые, содержащие одни и те же спин-орбитали и отличающиеся только порядком электронных координат и порядком индексов

101

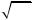
i1,i2 ,...,iN при коэффициентах ci1 i2 ...iN , то получим слэтеровский детерминант, построенный на рассматриваемых спин-орбиталях и умноженный на общий коэффициент ±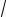N ! | ci1 i2 ...iN |. Набор N индексов {ij} называют I-ой упорядоченной конфигурацией, если индексы ij образуют возрастающую последовательность

гильбертовом пространстве, то детерминанты, соответствующие всем построенным на этих функциях упорядоченным конфигурациям, образуют полный набор в линейном пространстве антисимметричных N-электронных функций. Поскольку предполагается, что одноэлектронные функции ортонормированы, то и построенные на них детерминанты также ортонормированы.

Если взять с самого начала конечное число спин-орбиталей ψi (i =1,2,..., N ) ,

то детерминанты, соответствующие упорядоченным конфигурациям этих орбиталей, образуют полный базис в пространстве антисимметричных волновых функций, которые можно построить из данного набора одноэлектронных функций. Такое разложение волновых функций по детерминантам принято называть конфигурационным взаимодействием (КВ). На практике метод КВ заключается в вариационном определении коэффициентов разложения cI и сводится к решению задачи на собственные

значения с нахождением, как правило, лишь нескольких наименьших собственных значений, в нашем случае наинизших энергий молекулы.

Оператор Борна – Оппенгеймера содержит сингулярность rij−1 → ∞ (rij → 0) . С

другой стороны, разложение КВ не содержит межэлектронных расстояний в явном виде, поскольку используются только одноэлектронные спин-орбитали. Это означает, что поведение волновой функции в области пространства координат всех электронов, отвечающей сближению только двух их них, описывается только как суммарный эффект большого числа слагаемых в разложении КВ, вследствие чего ряд КВ сходится весьма медленно, особенно когда речь идет о локальных свойствах волновой функции.

102

2.7.1. Теорема Несбета

На практике почти все методы КВ строятся на волновой функции ОХФ или НХФ в качестве состояния отсчета. Конфигурации I соответствуют детерминантам, построенным на занятых и виртуальных орбиталях ХФ. Пусть Ψ0 обозначает волновую функцию ХФ. Запишем корреляционную

(промежуточную) нормировку функции

где равенства (154) следуют из ортонормированности занятых и виртуальных орбиталей ХФ, ведущей к

а после умножения этого равенства на Ψ0 и интегрирования с учетом (155) имеем:

Детерминанты ΨI построены на занятых и виртуальных хартри-фоковских

орбиталях и их можно идентифицировать по числу спин-орбиталей, которые заменены виртуальными по отношению к состоянию отсчета, т. е. по отношению к волновой функции ХФ Ψ0 . Другими словами, имеем одно-, двух-,

трехкратно и т. д. до N-кратно замещенных, где N есть число электронов в молекуле. Пусть ΨI – однократно возбужденные детерминанты. Их матричные

103

элементы по теореме Бриллюэна (§ 2.2.1) Ψ0 | Hˆ | ΨI = 0 . Для детерминантов с тремя и более возбуждениями относительно вакуумного состояния Ψ0

матричные элементы зануляются в соответствии с правилами Слэтера (§ 1.3.2). Единственные слагаемые, дающие ненулевой вклад в правую часть (189), это двухкратно возбужденные детерминанты. Обозначим их как

а соответствующие коэффициенты разложения в конфигурационном ряду (153) как cijuv , получим следующее выражение для корреляционной энергии:

(зан.) (вирт.)

= ∑ ∑ cijuv (ψi (1)ψ j (2) | r12−1 |ψu (1)ψv (2) − ψi (1)ψ j (2) | r12−1 |ψv (1)ψu (2) ),

i< j u<v

где интегралы берутся по спин-орбиталям, включая и интегрирование по спинам.

Теорема Несбета гласит: вычисление точной корреляционной энергии сводится к знанию только коэффициентов при дважды возбужденных конфигурациях в точном разложении КВ.

Энергию корреляции, очевидно, можно представить в виде

(зан.)

∆E = ∑ εij ,

i< j

где суммирование ведется по занятым хартри-фоковским орбиталям. Другими словами, энергия корреляции есть сумма вкладов

(вирт.)

εij = ∑ cijuv (ψi (1)ψ j (2) | r12−1 |ψu (1)ψv (2) − ψi (1)ψ j (2) | r12−1 |ψv (1)ψu (2) ),

u<v

которые получили название парных корреляционных энергий отдельных пар занятых спин-орбиталей. Каждая такая парная корреляционная энергия зависит также от всех других орбиталей, поскольку на значения коэффициентов

влияют все конфигурции в разложении КВ.

Различают внутрипарную корреляцию и межпарную корреляцию электронов. Внутрипарная корреляция реализуется тогда, когда у двух спинорбиталей пространственная часть одна и та же, заселенная электронами со спином α и β . Если же пространственные части разные, то речь идет о

104

межпарной корреляции. Вклады внутрипарной корреляции превалируют, поскольку они соответствуют паре электронов, которые в методе ХФ занимают одну и ту же пространственную орбиталь, результатом чего является бóльшая вероятность того, что два электрона окажутся близко друг к другу. В теории атомов аналогичным образом вводят внутриоболочечные и межоболочечные корреляции.

Корреляционная энергия инвариантна относительно унитарных преобразований занятых орбиталей, тогда как отдельные парные корреляционные энергии, естественно, не инвариантны. Вместе с тем, как ∆E , так и εij инвариантны относительно унитарных преобразований виртуальных

орбиталей.

2.7.2. О полном и усеченном КВ

Многоэлектронные функции в качестве базисных в методе КВ обычно берутся не в виде отдельных детерминантов, а в виде их комбинаций, представляющих собой чистые спиновые функции как собственные функции операторов Sˆz и Sˆ2 , а также соответствующих пространственной симметрии

молекулы, если таковая имеется. Это существенно снижает размерность задачи на собственные значения.

Если учитывают все приведенные по спину конфигурации, которые можно построить для данного одноэлектронного базиса, то говорят о полном конфигурационном взаимодействии (ПКВ/FCI), которое является точным решением вариационной задачи в выбранном базисе одноэлектронных функций. Используемый базис фактически определяет некую модельную задачу с соответствующим модельным гамильтонианом, и метод ПКВ дает точное решение уравнения Шредингера для этого модельного гамильтониана.

С увеличением числа электронов и размера базиса число детерминантов растет очень быстро. Поэтому полное КВ удается реализовать только для сравнительно небольших молекулярных систем. Подобные расчеты важны прежде всего с методологической точки зрения, поскольку они определяют эталоны для сравнения с ними результатов других приближенных методов расчета.

Из теоремы Несбета (§ 2.7.1) следует, что кроме детерминанта основного состояния молекулярной системы наиболее важными являются детерминанты дважды возбужденные. Если бы мы знали их точные коэффициенты разложения в полном ряду КВ, то могли бы вычислить и корреляционную энергию и точную энергию полного КВ.

105

Простейшим методом КВ, казалось бы мог быть учет только двухкратно возбужденных состояний в дополнение к волновой функции основного состояния, поскольку однократно возбужденные состояния с основным не взаимодействуют (теорема Бриллюэна). Однако, каждая однократно возбужденная конфигурация взаимодействует с несколькими двухкратно возбужденными, и их влиянием на оценку корреляционной энергии нельзя пренебречь. Обычно учитывают все однократно возбужденные конфигурации, поскольку их значительно меньше, чем двухкратно возбужденных, и учет их лишь незначительно увеличивает время счета.

Учет одновременно всех однократно и всех двухкратно возбужденных конфигураций (метод КВОД/CISD) позволяет учесть весьма значительную часть энергии корреляции. Нужно, однако, помнить, что такой подход размерно не согласован. Если взять две невзаимодействующих системы и каждую из них описать методом КВОД в качестве подсистемы общей объединенной системы, то волновая функция всей системы должна быть антисимметризованным произведением волновых функций обеих подсистем. Однако, такое произведение двух волновых функций КВОД не является волновой функцией типа КВОД, поскольку оно содержит такие слагаемые, которые формально соответствуют трех- и четырехкратным возбуждениям, не включающимся в описание типа КВОД объединенной системы. Разработаны, однако, приближенные поправки на размерную согласованность.

В принципе, необходимо помнить, что никакой усеченный ряд КВ никогда не будет размерно согласованным. Уже выполненные расчеты с учетом КВ, близким к полному, показывают, что учет возбуждений вплоть до четырехкратных дает ответ с достаточно малой ошибкой за счет размерной несогласованности.

Далее рассмотрим математический формализм вторичного квантования в применении к методу КВ. Электронные конфигурации трактуются как системы частиц и дырок на фоне вакуумного состояния, построенного из замкнутых оболочек основной конфигурации молекулярной системы. Выводятся выражения для операторов основных физических величин с использованием дырочного формализма, обобщенного для произвольной ортонормированной системы орбиталей. Сформулированы правила действия оператора Sˆ2 в представлении вторичного квантования. Применение теорем Вика для расчета матричных элементов между конфигурациями позволило нам сформулировать простую логическую схему вычислений в методе КВ, которая справедлива для конфигураций произвольной сложности и может быть легко запрограммирована.

В качестве примера такого общего подхода получены выражения для

106

матричных элементов операторов физических величин на однократно и двухкратно возбужденных конфигурациях для молекул и радикалов, а также приведены основные результаты расчета полного КВ для семиэлектронной π-системы бензильного радикала С6Н5СН2. Дадим вывод и приведем основные результаты для матриц электронной и спиновой плотности для синглетных и триплетных состояний молекул с учетом всех однократно и двухкратно возбужденных конфигураций детерминантным методом Слэтера.

2.7.3.Configuration Interaction in the Second Quantization Representation: Basics with Applications to Benzyl Radical up to Full CI

2.7.3.1.Introduction

The main advantage of the configuration interaction (CI) method [1] is the possibility of improving a trial wave function by extending considerably a set of basis configurations. The simple analytical expressions for the matrix elements of the Hamiltonian over the singly excited singlet and triplet configurations are well known. Thus an interaction of these configurations became a standard method for computing excited states of molecules [2]. Similarly, an interaction between singly excited configurations is frequently used for the calculation of the electronic structure of radicals [3], while doubly excited configurations have been used occasionally. Finally, not much is still known about contributions of configurations involving an excitation of three and more electrons [4].

Development of the expressions for the CI matrix elements can be considerably simplified when the second quantization formalism [5] is used instead of the usual method based on superposition of determinants [1]. The former approach has been used in order to obtain the matrix elements over the doubly excited singlet configurations [6]. A comparison with the corresponding elements over singly excited configurations shows that the expressions for the CI matrix elements become progressively complicated as configurations become more complex. The necessity to include more and more complicated formulae into the computer program is the main obstacle to a wider use of the extended configuration sets. In order to overcome these difficulties it is necessary to abandon the derivation of the analytical expressions for the matrix elements and to delegate this work to a computer at an early stage of the calculation. The simple rules to compute the matrix elements in the second quantization representations which follow from Wick’s theorem [7] and are also good for configurations of an arbitrary complexity need to be programmed. The present review is devoted to an actual realization of the above suggestion [8, 9]. Since the second quantization formalism has been described by many authors [5] we shall give only those formulae and statements which are necessary for our discussion.

107

In CI computations one first includes those configurations which do not differ much from the ground configuration. For example, the singly excited configurations are constructed from the Slater determinants built from the ground state determinant by changing a single row. To account for only the changes in an explicit form in the many-particle SCF theory, an elegant mathematical apparatus known as hole formalism has been developed. Besides offering a simple physical interpretation, the hole formalism reduces the calculations considerably. This formalism generalized on an arbitrary orthonormal orbital set will be exposed below.

2.7.3.2. The Second Quantization and CI Method

Let us consider a system of electrons in an external field, e.g. in a field of fixed nuclei. The Hamiltonian of this system is represented by a sum of one electron operators hˆ (k) , each of which acts on coordinates of one of the electrons and contains its kinetic energy operator and the external field potential, and a sum over all possible pairs of electrons of the electron interaction operators . Let be given a complete orthonormal set of orbitals ϕ1,ϕ2 ,ϕ3,.... Multiplying each orbital ϕi in turn by the spin functions η+ and η− which are eigenfunctions of the spin angular momentum

108

Acting on the vacuum state by each of the creation operator one obtains all oneparticle states

The states with two electrons are generated by operator Aˆ+jσ′ acting on the state

iσ

It follows from the anticommutation relations (161) that only those vectors are linearly independent and not equal to zero for which i = j and σ = σ′ are not valid simultaneously.

Following this procedure we obtain a set of linearly independent states with an arbitrary number of electrons

each one of its eigenvectors belongs to one of the subspaces RN of the space R built

109