
Yuriy Kruglyak. Quantum Chemistry_Kiev_1963-1991
.pdfмолекулы. Это связано с тем, что заданный набор конфигураций с увеличением n включает в себя все меньшую долю конфигураций, возможных при данном n. В то же время с увеличением n становится все более ощутимым выйгрыш в энергии, получаемой при переходе от простого КВ к самосогласованному решению при том же наборе конфигураций.
Наибольший эффект от оптимизации орбиталей достигается при малых наборах конфигураций. Для наборов Sn величина учитываемой части энергии корреляции также заметно увеличивается при переходе от ХФ орбиталей к орбиталям, самосогласованным для набора Sn . Однако практически те же результаты получаются также при учете КВ для набора Sn с использованием орбиталей, самосогласованных для меньших наборов S1 или S2 .
Для анализа полученных закономерностей установим связь поправки к энергии с числом заполнения орбиталей. Для всех рассматриваемых систем основная конфигурация вносит в основное состояние доминирующий вклад. Поэтому корреляционная добавка к ХФ энергии EHF ≡ ES0 (S0 ) с хорошей
точностью определяется во втором порядке теории возмущений (Приложение П-5), а именно:
ˆ |
2 |
ˆ |
ˆ |
) . |
(389) |
E = Ψ0 | H | Ψ0 |
− EHF − ∑ Tl |
( Ψl | H | Ψl − Ψ0 |
| H | Ψ0 |
||
|
l(≠0) |
|
|
|
|
Конкретизируя обозначения для рассматриваемых наборов конфигураций, получаем
ESq |
(Sr ) = ES0 |
2 |
ˆ |
(Sr )]. (390а) |
(Sr ) − ∑ ∑ Tkp[ Ψkk,pp (Sr ) | H | Ψkk,pp (Sr ) − ES0 |
||||
|
|
k(≤n) p(>n) |
|
|
Выражение в квадратных скобках является разностью между энергией конфигурации, соответствующей переходу пары электронов с орбитали k на орбиталь p , и энергией основной конфигурации. Для приближенной оценки второй суммы будем считать это выражение приближенно равным 2(εp −εk ) , где
величины εi могут рассматриваться как параметры, играющие роль эффективных одноэлектронных энергий. Выполнив эту замену, получим:
ES (Sr ) ≈ ES (Sr ) −2
q 0
∑ |
εp ∑ Tkp2 − |
∑ εk |
∑ Tkp2 |
|
|
. |
(390б) |
||||
p(>n) |
k(≤n) |
k(≤n) |
p(>n) |
|
|
Заменив εp и εk под знаком суммы средними значениями и обозначив разность этих средних через ε , с учетом (388) получаем
190

ES |
(Sr ) ≈ ES (Sr ) −2εn(u) , |
(390в) |
q |
0 |
|
где n(u) является суммой чисел заполнения орбиталей, не входящих в основную конфигурацию, а именно:
n(u) = ∑ np = ∑ ∑ Tkp2 . |
(391) |
|
p(>n) |
p(>n) k(≤n) |
|
Значения ES0 (Sr ) представлены в первом столбце табл. 11. Как видно из этой
таблицы, всегда положительный первый член в (390) вносит незначительный вклад в корреляционную добавку к энергии, и величина последней в основном определяется отрицательным вторым членом.
Сопоставление значений ESq (Sr ) из табл. 11 с рассчитанными значениями n(u) , представленными в табл. 12, показывает, что значения ε для наборов S1 , S2 и Sn лежат соответственно в пределах
3.3 − 3.9, |
4.3 − 4.7, |
4.9 − 5.5 |
при |
2n = 6, |
2.9 − 3.3, |
3.8 − 4.4, |
4.6 − 5.9 |
при |
2n = 8, |
2.7 − 3.8, |
4.1 − 4.3, |
5.1 − 6.4 |
при |
2n = 10. |
|
|
|
Таблица 12 |
|
Значения n(u) (391) для основного состояния
полиенов с числом углеродных атомов 2n, рассчитанные в МК приближении с набором конфигураций А, построенном на орбиталях, самосогласованных для набора конфигураций В
2n |
A → |
S1 |
S2 |
Sn |
B ↓ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S0 |
0.02933 |
0.02750 |
0.02663 |
6 |
S1 |
0.04012 |
0.04177 |
0.04220 |
S2 |
|
0.04259 |
0.04278 |
|
|
|
|||
|
Sn |
|
|
0.04019 |
|
S0 |
0.02588 |
0.02411 |
0.02322 |
8 |
S1 |
0.04498 |
0.04575 |
0.04443 |
S2 |
|
0.04141 |
0.04228 |
|
|
|
|||
|
Sn |
|
|
0.04032 |
|
S0 |
0.02183 |
0.02056 |
0.01999 |
10 |
S1 |
0.03905 |
0.04103 |
0.04284 |
S2 |
|
0.04281 |
0.04490 |
|
|
|
|||
|
Sn |
|
|
0.04153 |
Как видно из приведенных данных, средняя величина эффективной энергии перехода увеличивается при расширении набора конфигураций, что
191
связано с учетом все более высоколежащих переходов. Принимая во внимание приближенное постоянство ε для данного набора конфигураций, можно утверждать, что значительный выигрыш в энергии при оптимизации орбиталей достигается за счет существенного увеличения величины , т. е. в конечном
итоге за счет увеличения абсолютной величины коэффициентов Tkp .
Вобщем случае связь корреляционной поправки к энергии с коэффициентами при конфигурациях не является такой простой, как для рассмотренных наборов конфигураций. Однако из (389) следует, что при самосогласовании орбитали должны изменяться таким образом, чтобы повышение энергии основной конфигурации с избытком компенсировалось увеличением по абсолютной величине отрицательной добавки за счет увеличения вклада в волновую функцию остальных конфигураций. Выполненный расчет основного состояния урацила с учетом кроме основной конфигурации всех синглетных однократно возбужденных конфигураций служит показательной иллюстрацией такого вывода. Очевидно, что орбитали, самосогласованные для основной конфигурации, удовлетворяют также вариационным уравнениям МК теории ССП с указанным набором конфигураций, так как при этом, согласно теореме Брилюэнна (§ 2.2.1), вклад в основное состояние однократно возбужденных конфигураций равен нулю. В то же время учет однократно возбужденных конфигураций на хюккелевских орбиталях приводит в ряде случаев к энергии основного состояния более низкой, чем хартри-фоковская энергия. По этой причине представлялось интересным найти самосогласованные орбитали, реализующие минимум энергии основного состояния урацила с набором всех однократно возбужденных конфигураций.
Вкачестве начальных были взяты орбитали, получающиеся из хюккелевских после одного цикла самосогласования для основной конфигурации. Таким образом, исходные величины Vkm были малыми, однако,
не строго равными нулю. Для получения самосогласованных решений использовался ОГ (387) с λ =1 / 30 . Ход процесса самосогласования иллюстрируется кривыми, приведенными на рис. 9.
Как видно из этого рисунка, вначале медленное, а затем все более быстрое изменение орбиталей сопровождается увеличением энергии основной конфигурации при одновременном резком увеличении вклада однократно возбужденных конфигураций, что приводит в конечном итоге к существенному понижению энергии основного состояния. Окончательная величина корреляционной добавки к энергии получилась равной –0.5334 эВ.
192
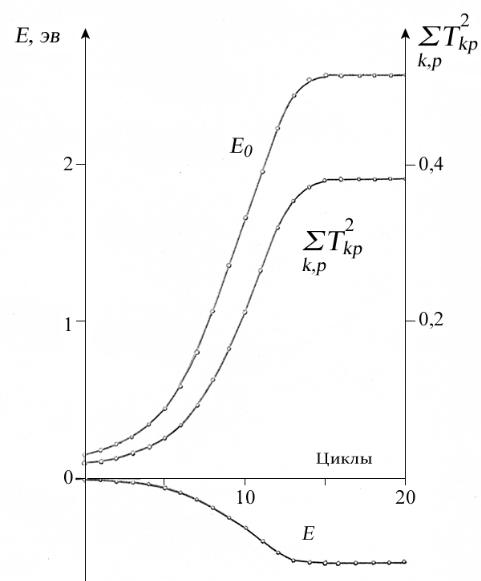
Рис. 9. Ход процесса самосогласования для основного состояния урацила с учетом всех однократно возбужденных конфигураций. За начало отсчета энергии основной конфигурации Е0 и энергии состояния Е принята хартрифоковская энергия.
Основное состояние урацила было рассчитано также в двухконфигурационном приближении с набором конфигураций S1 .
Корреляционная добавка к энергии, полученная на орбиталях, самосогласованных для основной конфигурации, оказалась равной –0.2469 эВ. Самосогласование орбиталей приводит к возрастанию этой добавки до –0.6198 эВ. К сожалению, нет данных, которые позволили бы оценить энергию корреляции в урациле. Однако, величина корреляционной добавки, значительно бóльшая соответствующей величины для полиена, дает основание утверждать, что выигрыш в энергии за счет оптимизации орбиталей в гетероатомной
193
системе значительно больше, чем в регулярном полиене с тем же числом электронов.
В расчете дублетного основного состояния бензильного радикала использовался конфигурационный набор, включающий кроме основной конфигурации все однократно возбужденные конфигурации симметрии 2B2 ,
т. е. набор конфигураций, который обычно используется при вычислении спиновой плотности. Расчет методом КВ с этим набором конфигураций, построенном на орбиталях, самосогласованных для основной конфигурации, приводит к энергии на 0.1696 эВ ниже самосогласованной энергии основной конфигурации. При оптимизации добавка к самосогласованной энергии основной конфигурации равна –0.3909 эВ, что составляет около 42 % вычисленной в § 2.7.3.7.1 энергии для бензильного радикала в модели ППП.
Приведенные выше результаты иллюстрируют ряд закономерностей, связанных с переходом от несамосогласованных МК волновых функций к самосогласованным. Эти закономерности имеют общий характер и должны проявляться при учете электронного взаимодействия в любой модели, независимо от способа вычисления базисных интегралов.
Оптимизация орбиталей в МК волновой функции приводит к ее существенному улучшению, несмотря на то, что использованные небольшие наборы АО ограничивали в значительной степени возможные вариации. Симметрия и альтернантность полиенов и бензильного радикала накладывали дополнительные ограничения на вариации орбиталей, поэтому для нерегулярной системы с гетероатомами поправки к энергии оказались значительно бóльшими.
Количественные оценки, полученные для сопряженных систем, разумеется, не применимы к неэмпирическим моделям. Следует, однако, ожидать, что в неэмпирических расчетах молекул, где обычным стало использование базиса в несколько десятков и даже сотен АО, оптимизация орбиталей в МК волновой функции даст особенно большой эффект. Нахождение самосогласованного решения при малых наборах конфигураций не связано с большими дополнительными затратами машинного времени. Полученную волновую функцию можно при необходимости улучшить далее, расширяя набор конфигураций без проведения самосогласования. Такой путь уточнения волновых функций является наиболее эффективным.
194
2.8.2.2.7.2. Молекула LiH ab initio
2.8.2.2.7.2.1. К постановке задачи
Ставится задача построения потенциальной кривой и вычисление ряда таких свойств молекулы гидрида лития как равновесное расстояние, дипольный момент, спектроскопические константы. При решении этой задачи наряду с апробацией метода ОГ в неэмпирическом приближении ставилась также цель исследовать возможности МК теории ССП для построения потенциальной функции с учетом корреляционных эффектов, что существенно для молекулы LiH, диссоциирующей гомолитически на атомы с открытыми оболочками.
Четырехэлектронная молекула LiH описывалась гамильтонианом в приближении Борна – Оппенгеймера. При таком подходе для построения потенциальной функции нужно решать электронную задачу для ряда значений межъядерного расстояния.
Молекула LiH исследовалась методами квантовой механики многими авторами. Однако в подавляющем большинстве исследований, обширная библиография которых приведена в [48, 49], электронная структура этой молекулы изучалась при равновесном межъядерном расстоянии или вблизи него, и есть лишь следующие публикации [48, 50 – 55], содержащие полные результаты расчета потенциальной кривой и спектроскопических констант.
Кейдом и Хао [48] потенциальная кривая молекулы LiH рассчитывалась в одноконфигурационном приближении ХФР в интервале изменений межъядерного расстояния R от 2 до 4.2 ат. ед. Использование расширенного базиса атомных функций слэтеровского типа с оптимизацией экспонент позволили авторам практически достичь хартри-фоковского предела. Для тех спектроскопических констант, которые определяются поведением потенциальной кривой в области минимума, они получили хорошее согласие с экспериментом. Однако с ростом R резко увеличивается энергия корреляции, поэтому в приближении ХФ невозможно получить удовлетворительного значения энергии диссоциации этой молекулы.
Учет корреляционных эффектов в волновой функции обеспечивает получение более реалистичных потенциальных кривых. Так, поведение потенциальной кривой молекулы LiH, полученной Каро [50] при использовании метода КВ, показывает, что волновая функция в таком приближении описывает образование молекулы лучше, чем одноконфигурационная функция Кейда и Хао. Однако минимум энергии у Каро расположен гораздо выше, чем минимум у Кейда и Хао, что связано в первую очередь с минимальной размерностью базиса атомных функций, использованных Каро для разложения МО. Существенное улучшение
195
положения потенциальной кривой, построенной с помощью метода КВ, удалось получить лишь при расширении базисного набора и при значительном увеличении числа членов конфигурационного разложения волновой функции
[52 – 54].
Иная процедура для учета корреляционных эффектов использовалась в работах [51, 55], в которых для построения потенциальной кривой LiH волновая функция записывалась в виде антисимметризованных произведений сильно ортогональных двухэлектронных функций. Полученные таким образом потенциальные кривые оказались почти совпадающими с кривыми [50, 53], рассчитанными методом КВ при соответствующих базисах.
В работах [53 – 55] получены достаточно точные результаты, однако, использованные в них методы требуют значительных вычислительных мощностей. В этом смысле более приемлемыми являются методы МК теории ССП. К молекуле LiH такой подход применялся лишь в работе (39), однако, только при равновесном межъядерном расстоянии.
При расчете потенциальной кривой и ряда свойств LiH в основном состоянии в работах [42, 46] использовался метод ОГ (§ 2.8.2.2), применение которого обеспечивает получение решений вариационных уравнений МК теории ССП, соответствующих минимуму энергетического функционала. Чтобы уменьшить ограничения на возможные вариации орбиталей при их оптимизации, использовался расширенный базисный набор из 16 атомных орбиталей. Для более корректного определения спектроскопических констант энергетические характеристики рассчитывались для 18 межъядерных расстояний в интервале от 2 до 8 ат. ед., а также при бесконечном разведении ядер; при этом плотность точек на потенциальной кривой в области минимума была значительно увеличена.
Как для гетероядерной молекулы, прослеживалось не только изменение энергии молекулы LiH при разведении ядер, но и изменение ее дипольного момента, поскольку значение его характеризует распределение электронной плотности. Кроме того, у молекул LiH есть две оболочки и поэтому она является хорошим объектом для рассмотрения особенностей применения МК теории ССП для учета внутриоболочечной корреляции (§ 2.7.1) в валентной и внутренней оболочках одновременно. Рассматривалась также структура полученных многоконфигурационных функций.
196

2.8.2.2.7.2.2. Методика расчета
Волновая функция основного состояния молекулы LiH записывалась в виде разложения (273) по следующим трем одноконфигурационным функциям:
|
|
Ψ0 |
=|ψ1ψ |
1ψ2ψ |
2 |, |
(392а) |
|
|
|
Ψ1 |
=|ψ1ψ |
1ψ3ψ |
3 |, |
(392б) |
|
Спинорбитали ψi и ψ |
|
Ψ2 =|ψ4ψ |
4ψ2ψ |
2 |. |
(392в) |
||
i |
представляли собой произведения орбитали | i σ-типа на |
||||||
спиновые функции α |
и β , соответственно, т. е. угловая |
корреляция не |
|||||
рассматривалась. В этом случае нормированные слэтеровские детерминанты (392) являются синглетными собственными функциями оператора Sˆ2 , и построенная таким образом волновая функция молекулы Ψ соответствует состоянию X 1Σ+ .
Если в качестве основной принять конфигурацию Ψ0 , то двухкратно возбужденные по отношению к ней конфигурации Ψ1 и Ψ2 позволяют учесть
корреляцию электронов в валентной и внутренней оболочках, соответственно. Выбранный таким образом набор конфигураций дает возможность учесть в волновой функции внутриоболочечную корреляцию, которая по сравнению с межоболочечной корреляцией является определяющей [56].
Молекулярные орбитали выбирались в виде разложения (358) по базисному набору атомных функций слэтеровского типа
|
|
(2ς |
µ |
)2nµ +1(2l |
µ |
+1)(l |
µ |
−m )! |
|
|
nµ −1 −ςµr |
|
|mµ| |
|
imµϕ |
|
|||
|
|
|
|
|
|
µ |
|
|
|
|
|
||||||||
| µ ≡|nµlµmµςµ = |
|
|
|
|
|
|
|
|
r |
|
|
e |
P |
|
(cosθ)e |
|
, (393) |
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
4π(2nµ )!(lµ +mµ )! |
|
|
|
|
|
lµ |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
где r , θ и ϕ – сферические координаты, |
nµ ,lµ ,mµ |
|
– квантовые числа µ -ой АО, |
||||||||||||||||
P|mµ |(cosθ) – присоединенный полином Лежандра, |
|
ς |
µ |
– орбитальная экспонента. |
|||||||||||||||
lµ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Используемый в расчетах базисный набор приведен в табл. 13.
У всех 16 атомных функций магнитное квантовое число m полагалось равным нулю. Таким образом, все МО относились к σ-типу и угловая корреляция электронов в расчетах не учитывалась.
Приведенные в табл. 11 значения орбитальных экспонент ς найдены Кейдом и Хао [48] в результате минимизации самосогласованной хартрифоковской энергии основного состояния молекулы LiH при равновесном межъядерном состоянии. Эти же авторы показали, что при расчетах потенциальных кривых дополнительная оптимизация базисного набора лишь
197
незначительно отражается на результатах. В работе [56] при использовании МК теории ССП также было найдено малое различие в орбитальных экспонентах для равновесного межъядерного расстояния и для случая разведенных атомов. С другой стороны, опыт расчетов двухатомных гомоядерных молекул свидетельствует о том, что базисный набор АО, оптимизированный в приближении ХФР, при переходе к многоконфигурационному приближению практически не требует корректировки. Поэтому базисный набор, приведенный в табл. 13, использовался для всех межъядерных расстояний.
Таблица 13 Базисный набор* слэтеровских орбиталей
Кейда и Хао [48]
|
ν |
n |
l |
ς |
ν |
|
n |
|
l |
ς |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
0 |
2.52117 |
9 |
|
3 |
|
1 |
3.20000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
0 |
4.69900 |
10 |
|
3 |
|
2 |
0.64232 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
2 |
0 |
0.79722 |
11 |
|
3 |
|
2 |
1.20000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
2 |
0 |
1.20000 |
12 |
|
4 |
|
3 |
0.92480 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
3 |
0 |
2.75000 |
13 |
|
1 |
|
0 |
0.88775 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
2 |
1 |
0.73691 |
14 |
|
1 |
|
0 |
1.56567 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
2 |
1 |
1.20000 |
15 |
|
2 |
|
0 |
1.20000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
2 |
1 |
2.75000 |
16 |
|
2 |
|
1 |
1.37646 |
|
|
|
|
|
|
|
|
|
|
|
||
|
*АО с |
ν =1 →12 |
соответствуют атому Li, |
||||||||
|
|
|
|
остальные – атому Н. |
|
|
|||||
Необходимые для расчетов одно- и двухэлектронные интегралы на |
|||||||||||
базисных функциях |
(380) |
вычислялись |
|
по |
алгоритму, разработанному |
||||||
В. А. Куприевичем, О. В. Шрамко и В. Е. Клименко и встроенному в программу расчетов по МК теории ССП [59].
Среднее значение кинетической энергии электронов и электронная
составляющая дипольного момента µel |
в МК приближении при фиксированном |
|
значении R вычислялись по формуле |
|
|
Ω = ∑γ (i | j)∑Cµ jCνi ωµν , |
(394) |
|
i, j |
µ,ν |
|
198
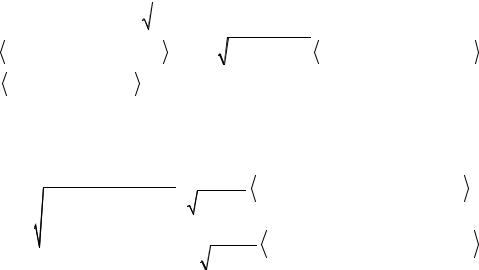
где Ω – искомое среднее значение, γ (i | j) – элементы одночастичной матрицы плотности (317), Cµi – коэффициенты разложения (358) орбиталей по фиксированному базису, а ωµν – либо элементы матрицы кинетической энергии
|
|
|
4 |
(nµ + lµ )(nµ − lµ −1)/ 2nµ (2nµ −1)(2nµ − 2)(2nµ − 3)× |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tµν = − |
2 |
nµ − 2,lµmµ ςµ |
|
nν lν mν ςν |
− 4nµ / 2nµ (2nµ −1) nµ −1,lµmµ ςµ |
|
nν lν mν ςν |
|
,(395) |
|||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||
2 |
ςµ |
× |
|
|
+ |
|||||||||||||||||||||||||||
|
|
|
nµlµmµ ςµ |
|
nν lν mν ςν |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
либо элементы матрицы дипольного момента |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lµ +1 |
nµ +1,lµ +1,mµ ςµ |
|
nν lν mν ςν |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
dµν = |
1 (nµ +1)(nµ +1/ 2) |
2lµ +3 |
|
|
|
|
|
|
|
|
|
|
. (396) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
(2lµ +1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
ςµR |
|
|
|
|
lµ |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
+ |
|
|
nµ +1,lµ −1,mµ ςµ |
|
nν lν mν ςν |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2lµ −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Величина потенциальной энергии вычислялась как разность между полной |
||||||||||||||||||||||||||||||||
и кинетической энергиями молекулы. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Оптимизация |
коэффициентов |
|
Cµi в |
задаче вида |
|
(361) проводилась |
||||||||||||||||||||||||||
улучшенным методом ОГ первого приближения (§ 2.8.2.2.5) с матричными элементами (357) и (344).
Для апробации алгоритма воспроизводился ряд точек потенциальной кривой, построенной Кейдом и Хао [48] в приближении ХФР. Максимальное отличие обнаружилось в значениях энергии EHF на две единицы в шестой
значащей цифре, которое, вероятно, связано с небольшими отличиями в значениях базисных интегралов. Поскольку ХФ потенциальная кривая приведена в [48] лишь до значения R , равного 4.2 ат. ед., расчет был продолжен в том же приближении до R = 8 ат. ед.
Расчет волновой функции при бесконечном разведении ядер выполнялся с вычисленным на базисных функциях набором интегралов, в котором все двухцентровые интегралы занулялись. Обычная рутановская процедура самосогласования орбиталей, сходившаяся при конечных значениях R , в этом случае приводила к осцилляциям. Поэтому при R = ∞ для получения одноконфигурационного самосогласованного решения применялся, как и в многоконфигурационном случае, улучшенный метод ОГ первого приближения.
199
