
Yuriy Kruglyak. Quantum Chemistry_Kiev_1963-1991
.pdf
Рис. 4. Ход процесса самосогласования основного состояния урацила (а) и полиена (б) в одноконфигурационном приближении с использованием ОГ первого приближения (1), улучшенного ОГ первого приближения (1') и ОГ второго приближения (2).
Рис. 5. Ход процесса самосогласования нижнего триплетного состояния урацила (а) и полиена (б) в одноконфигурационном приближении с использованием ОГ первого приближения (1), улучшенного ОГ первого приближения (1') и ОГ второго приближения (2).
180
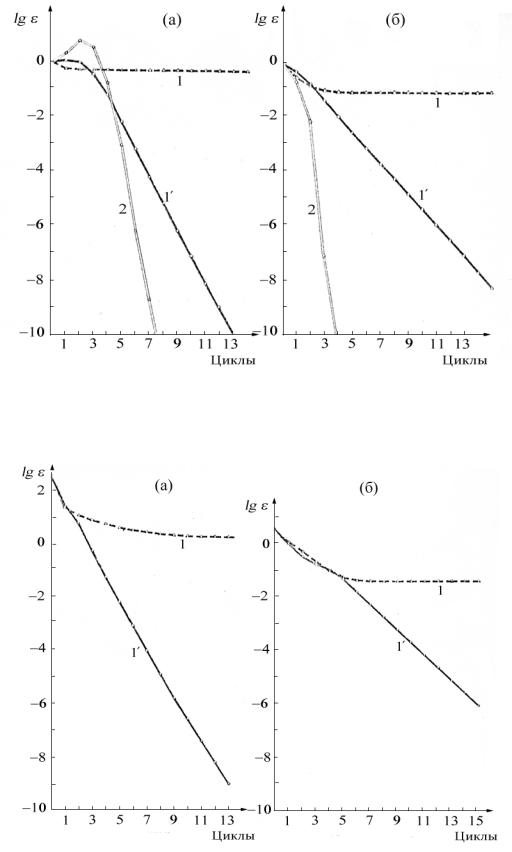
Рис. 6. Ход процесса самосогласования основного состояния урацила (а) и полиена (б) в двухконфигурационном приближении с использованием ОГ первого приближения (1), улучшенного ОГ первого приближения (1') и ОГ второго приближения (2).
Рис. 7. Ход процесса самосогласования основного состояния урацила (а) и полиена (б) с использованием ОГ первого приближения (1) и улучшенного ОГ первого приближения (1').
В волновую функцию кроме основной конфигурации входили 15 для урацила и 16 для полиена двухкратно возбужденных конфигураций. В качестве исходных орбиталей выбирались орбитали, диагонализующие хюккелевскую матрицу.
181

Рис. 8. Изменение спектра собственных значений матрицы вторых производных энергии в ходе процесса самосогласования с применением ОГ второго приближения для основного состояния урацила в одноконфигурационном (а) и двухконфигурационном (c) приближениях и первого триплетного состояния (b).
В ходе процесса самосогласования начало спектра сдвигается вправо, так что начиная со второго цикла все εp становятся положительными, что и должно
иметь место вблизи минимума. Начиная с третьего цикла спектр стабилизируется и, как видно из рис. 6а, отмечается особенно резкое ускорение сходимости, что соответствует уменьшению добавки κ2Vp2 в формуле (353).
Применение метода ОГ второго приближения, приводящее к резкому уменьшению числа циклов самосогласования, сопровождается одновременно значительным увеличением вычислительной работы, связанной с построением и диагонализацией матрицы вторых производных. Поэтому весьма полезным представляется использование улучшенного метода ОГ первого приближения, состоящего в пренебрежении смешанными вторыми производными энергии (§ 2.8.2.2.5). Результаты применения улучшенного метода ОГ первого приближения с оператором (357) также приведены на рис. 4 – 7. Сходимость этого метода в отличие от метода ОГ второго приближения имеет экспоненциальный характер, однако, как видно из графиков, скорость сходимости значительно выше, чем при применении метода ОГ первого приближения.
Спектры диагональных элементов Akmkm матриц вторых производных очень похожи на приведенные на рис. 8 спектры собственных значений этих матриц
183
