Yuriy Kruglyak. Quantum Chemistry_Kiev_1963-1991

функций, аппроксимирующего функцию 1s , 2s или 2 p атома водорода, к набору, аппроксимирующему соответствующую функцию атома углерода, нужно в соответствующей аппроксимации произвести замену

r 5.7r, (для функции1s)

r 3.25r. (для функций 2s и 2р)

Таким образом, коэффициентами, переводящими набор показателей экспонент гауссовых функций, аппроксимирующих собственную функцию атома Н, в набор показателей экспонент гауссовых функций, аппроксимирующих аналогичную собственную функцию атома С, будут 5.72 = 32.49 для функции 1s и 3.252 = 10.5625 для функций 2s и 2 p . В работе [38] таким образом был получен базис 7s3p гауссовых функций для атомов B, C, N, O, F. Было взято четырехчленное разложение по гауссовым функциям для функции 1s и трехчленные разложения для функций 2s и 2 p атома Н [28] и перемножением чисел на соответствующие коэффициенты получены предварительные наборы экспонент. Базис 7s должен быть общим как для функции 1s , так и для функции 2s . Серия предварительных поисковых расчетов с одним из наборов атома С привела к следующим выводам. Четыре экспоненты, полученные из четырехчленного разложения функции 1s атома Н должны быть объединены с двумя меньшими экспонентами, полученными из трехчленного разложения функции 2s атома Н, причем следует добавить седьмую, максимальную по величине экспоненту, примерно в три раза превосходящую ближайшую к ней. Для ясности, процесс получения показателей экспонент иллюстрируется в табл. 7.

Дальнейшие расчеты с набором гауссовых функций для атома С показали, что полученный набор 7s следует несколько «сжать» к центру, т. е. меньшие значения экспонент увеличить, а бóльшие – уменьшить примерно в 1.1 раза, и наоборот – экспоненты базиса 3р должны быть «раздвинуты», т. е. меньшая – уменьшена, а бóльшая – увеличена примерно в 1.3 раза. Все значения были округлены до 2 – 3 значащих цифр. Окончательные значения полученных таким образом показателей экспонент приведены в табл. 8.

Подчеркнем, что правила получения этих значений показателей экспонент установлены для одного атома и затем в готовом виде перенесены на все остальные. Таким образом, значения экспонент для последовательности атомов систематически получаются из значений экспонент для атома водорода.

280

Качество построенного таким образом базиса демонстрируется данными таблиц 9 и 10. В табл. 9 приведены орбитальные энергии и собственные векторы, полученные при расчете в базисе гауссовых функций 7s3p (табл. 8).

В табл. 10 приведены вычисленные значения полной энергии вместе с литературными данными. В третьем столбце этой таблицы приведены уже упоминавшиеся данные [40] по расчетам в базисе 7s3p из работы [31]. Хотя мы не занимались оптимизацией базиса, полученные нами значения, которые даны в четвертом столбце таблицы, лежат по энергии ниже. В следующем пятом столбце приведены лучшие из известных результатов по расчетам в базисе 7s3p

[41].

Таблица 7 Получение наборов показателей экспонент гауссовых базисных функций

для атомов второго периода*

* Значения показателей экспонент в левом столбце взяты из [28].

Первые три и последние три числа каждого следующего столбца таблицы получаются умножением соответствующих чисел левого столбца на квадрат слэтеровского показателя экспоненты для функций 2s и 2 p данного атома. Средние четыре числа каждого столбца

получаются умножением на квадрат слэтеровского показателя экспоненты для функции 1s данного атома.

**Эти показатели экспонент выбрасываются из набора 7s.

***Эти показатели экспонент включаются в набор 7s.

281

Базис 7s3p в этой работе был получен, как и базис Хузинаги [28] путем тщательной оптимизации значений экспонент. По утверждению авторов работы [41], понизить полученные ими значения энергии в базисе 7s3p более, чем на 0.01 ат. ед., невозможно. Сравнение этих значений с результатами, полученными в базисе Долгушина показывает, насколько оптимален последний. Как видим, предложенный выше алгоритм построения гауссова базиса приводит к получению близких к оптимальным базисных наборов, которые по желанию либо могут использоваться непосредственно, либо могут стать хорошей отправной точкой для тщательной оптимизации значений экспонент, минимизирующих полную энергию.

Таблица 8 Показатели экспонент базиса гауссовых функций 7s3p

для атомов второго периода

В этой же табл ице 10 в последнем столбце для сравнения приведены хартри-фоковские значения энергии [28]. Ошибка в полной энергии атомов, рассчитанных в базисе 7s3p составляет примерно 0.2% от ХФ значения энергии.

Если брать разное число гауссовых функций, описывающих собственные функции атома водорода, то можно установить соответствующие правила для получения базисов различной размерности для расчета атомов и молекул с заранее заданной точностью. Таким образом, использование аналога правил Слэтера в расчетах атомов методом разложения может стать вполне стандартной процедурой. Такая процедура имеет большие преимущества по сравнению с трудоемкими методами прямого поиска оптимальных значений экспонент гауссовых базисных функций.

282

Глава 5. Расчет электронной структуры молекул в ограниченных базисах безузловых гауссовых функций

5.1. Аппроксимация функций, обладающих выделенными осями симметрии, посредством сферических гауссовых функций

В предыдущей главе обсуждался расчет атомов в базисе сферически симметричных гауссовых функций вида

определенных в любой точке пространства А.

Таблица 9 Орбитальные энергии и коэффициенты разложения

для атомов второго периода, вычисленные в базисе гауссовых функций 7s3p (табл. 8)*

* Первое число каждого столбца – орбитальная энергия (ат. ед.), следующие числа – коэффициенты разложения, соответствующие гауссовому базису (табл. 8).

283

Поскольку, вообще говоря, единственное достоинство гауссовых функций

(1) заключается в простоте счета с ними молекулярных интегралов, то логично использовать это свойство с максимальной полнотой. В сводке формул для молекулярных интегралов (47/§3.1) с функциями (1) используется единственная неявно выраженная функция F0 (z) (31/§3.2) из семейства функций Fm (z) ,

связанного с функцией ошибок (m = 0) и ее производными (m > 0) . Формулы для

интегралов с декартовыми гауссовыми функциями общего вида (15/§3.1) намного более сложные. Достаточно сказать, например, что общая формула для двухэлектронного интеграла с декартовыми гауссовыми функциями р-типа есть сумма шестнадцати слагаемых, содержащих вспомогательные функции Fm

вплоть до F4 включительно [14].

Таблица 10 Полная энергия (ат. ед.) атомов второго периода, рассчитанная в различных гауссовых базисах 7s3p

вместе с хартри-фоковскими значениями

* Базис Долгушина (табл. 8). ** Хартри-фоковское значение.

Благоприятная возможность использовать в качестве базисных функций только функции (1), которые для этого должны быть специально расположены

впространстве и таким образом вычислять все встречающиеся интегралы только с помощью простых формул (47/§3.1), обусловлена тем обстоятельством, что количество центров расположения гауссовых функций (1)

впространстве не увеличивает объем вычисления с ними. Именно поэтому возникла идея о том, чтобы пользоваться только сферически симметричными функциями (1), а атомные функции, обладающие выделенной осью симметрии, строить из линейных комбинаций функций (1), расположенных вдоль этой оси симметрии. Эта идея была впервые высказана Прёйсом [42], а затем была подробно разработана Уиттеном [34, 44]. На рис. 4 представлена

аппроксимация pz-функции двумя гауссовыми функциями (1). Для того, чтобы определить р-функцию подобным образом, нужно знать показатель экспоненты функции (1), участвующей в образовании р-функции, и расстояние δ , на которое должны быть разнесены две одинаковые гауссовы функции.

284

Рис. 4. Аппроксимация функции pz двумя одинаковыми функциями (1):

N (GA −G−A ) = G( p) .

Для ответа на эти вопросы важным является следующее наблюдение [44]: при δ → 0 (рис. 4) комбинация GA −G−A переходит в истинную р-функцию с тем же показателем экспоненты. Следующая цепочка равенств убеждает нас в этом:

Итак, чтобы получить хорошую аппроксимацию р-функции, в выражении

(2) нужно брать достаточно малое значение δ и тот же показатель экспоненты, что и у истинной р-функции. Очевидно, что подобное утверждение остается в силе и при аппроксимации функций d- и f-симметрии, поскольку в соответствии с излагаемым подходом эти функции могут рассматриваться как построенные из линейных комбинаций р-функций. Таким образом, можно утверждать, что при аппроксимации атомных функций, обладающих выделенными осями симметрии, посредством сферически симметричных гауссовых функций (1) новой проблемы выбора показателей экспонент не возникает, но появляется проблема выбора сдвигов δ . Фактически параметром малости в (3) является не δ , а δ a ≡ γ , так что, строго говоря, мы должны

285

Результаты работ [44 – 47] подтверждают практическую эквивалентность функций (2) и (4) – при достаточно малых δ как радиальное [44 – 46], так и угловое [47] поведение функции (2) близко к поведению истинной р-функции, хотя, конечно, полностью эти функции совпадать не могут. Использование аппроксимации (2) должно приводить к зависимости результатов расчета от вращения координатных осей. Как будет показано далее, эта зависимость практически неощутима, если сдвиги δ выбраны правильно.

5.2. О программе ФУГА, о точности вычисления интегралов, выборе значений сдвигов и об инвариантности расчетов при поворотах осей координат

Молекулярная программа ФУГА М. Д. Долгушина [48] предназначена для расчета молекул с замкнутой оболочкой в синглетных состояниях. Текст этой программы на языке АЛГОЛ можно найти в [49].

В программе с самого начала предусмотрено, что базисной функцией может быть не только функция (1) сама по себе, но и любая фиксированная комбинация этих функций. Такую линейную комбинацию гауссовых функций

(1) будем называть группой. Конечно, группа может содержать всего один элемент – одну гауссову функцию. Размерность базиса определяется числом групп гауссовых функций. Обычно группы вводятся для сокращения размерности базиса, и линейные коэффициенты, с которыми функции (1) объединяются в группу, берутся из соответствующих атомных расчетов. В программе ФУГА введение групп необходимо еще по соображениям симметрии – ясно, что линейная комбинация (2) должна всегдарассматриваться как группа, которую нельзя декомпозировать.

Вернемся к вопросу о выборе сдвигов δ . Численное значение сдвига должно выбираться по формуле (5), причем, в принципе, чем меньше γ , тем лучше аппроксимация (2). Однако, здесь необходимо обсудить одну тонкость [50], которая легко может остаться незамеченной и, таким образом, привести к ошибкам, а именно: минимальное значение γ связано с точностью вычисления функции F0 (z) (31/§3.2). Для вычисления этой функции обычно используют

полиномиальные разложения [4, 51], которые, естественно, характеризуются определенной точностью. Например, разложение, приведенное в [4], имеет точность 4 10−6 во всей области изменения аргумента. Гораздо более точная формула приведена в работе [51]. Она дает максимальную ошибку 2.5 10−9 . Если для вычисления F0 пользоваться полиномиальным разложением из [4], то

286

при выборе γ < 0.1 возникают проблемы, связанные с недостаточной точностью счета интегралов вида

Когда aδ 2 мало, N – большое положительное число и, разлагая экспоненту и функцию F0 в ряд до первого порядка по aδ 2 , в квадратных скобках (7)

получим минус бесконечно малую величину второго порядка по aδ 2 . Положительный результат для существенно положительного интеграла (6) получается только при разложении до второго порядка по aδ 2 включительно.

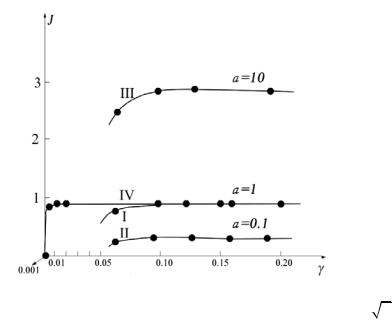
расчеты интеграла (6) позволили установить те минимальные значения aδ 2 = γ 2 , при которых вычисление интеграла (6) дает наверняка устойчивый результат. Результаты этих предварительных вычислений показаны на рис. 5.

Рис. 5. Вычисление интеграла J (6) для разных значений γ = δ a и разных

значений a . Для наглядности точки, соответствующие определенному значению интеграла, соединены линиями. Линии I, II, III соответствуют вычислениям с функцией F0 , точной до 10−6 , а линия IV – с функцией F0 ,

точной до 10−9 .

287

Из рис. 5 видно, что при вычислениях F0 с точностью 10−6 значение интеграла неустойчиво (начинает уменьшаться) при γ < 0.1; например, при γ = 0.02 значение интеграла при a =1 оказывается отрицательным). Безопасным

где в числителях этих формул значатся лишь нижние границы, и ничто не мешает использовать, например, формулу (8) при более точном вычислении F0 .

Значительный произвол в выборе константы γ в формуле для δ (5) можно понять и объяснить следующим образом [50]. Зададимся вопросом: до какого максимального значения δ соответствие в деталях между (2) и (4) сохраняется и не зависит от δ ? Например, максимум функции (2) имеет место при rmax =1/ 2a . Вычисление положения максимума функции (4) ведет к уравнению для rmax , а именно:

т. е. при достаточно малых δ положение максимума функции (4) совпадает с положением максимума функции (2).

288

которое, как известно, выполняется для довольно широкого интервала значений δ a = γ . Какое бы свойство функций (2) и (4) ни взять для сравнения, всегда при попытке определить δ мы прийдем к уравнению типа (11), которое утверждает, что при достаточно малых γ ничто от δ не зависит – функции совпадают и что это наблюдается в пределах изменения γ от нуля до таких значений, когда еще верно (11) с заданной точностью. Если потребовать, например, чтобы точность совпадения функций (2) и (4) или точность

обязательно соответствует более низкому значению полной энергии. Так, например, рассчитывая молекулу Н2О с высокоточной формулой для F0 ( 10−9 ),

приведена в табл. 11.

Таблица 11 Сравнение четырех расчетов молекулы Н2О с разным выбором сдвигов и с разной ориентацией относительно осей координат (ROH =1.8 ат.ед., HOH =105°)

*A – положительная полуось y делит внутренний HOH пополам; B – биссектрисы углов HOH и x0y совпадают.

Неизбежным недостатком аппроксимации p-, d-, f-функций посредством функций (1) является зависимость результатов расчетов от вращения системы координат. Однако, нужно отметить, что эта зависимость носит, так сказать, чисто умозрительный характер. В табл. 11 приведены результаты расчетов,

289